
上次课复习: 1、函数在一点连续的定义 (1)若Iim[f(x+△x)-f(x)]=lim△y=0 则称f(x)在点x,连续。 (2)若Vε>0,36>0,当x-xxo 2、间断点及其分类 第一类间断点:可去间断点;跳跃间断点。 第二类间断点:(非第一类间断点)无穷间断点;振 荡间断点
2、间断点及其分类 第一类间断点:可去间断点;跳跃间断点。 第二类间断点:(非第一类间断点)无穷间断点;振 荡间断点。 上次课复习: 1、函数在一点连续的定义 (1)若 则称 在点 连续。 (2) (3)若 ,则称 在点 x0 连续。 0 0 lim ( ) ( ) x x f x f x → = 0 0 若 当 时,恒有 − − 0, 0, ( ) ( ) x x f x f x 0 0 0 0 lim ( ) ( ) lim 0 x x f x x f x y → → + − = = f x( ) 0 x f x( )

§1.7闭区间上连续函数的基本性质 一、连续函数的和、差、积、商的连续性 定理1(四则运算)若函数f(x)和g(x)在点x。 连续,则 (1)f(x)±8(x)在点x,连续; (2)f(x)·8(x)在点x连续; (3) f() ,(g(x)≠0)在点x,连续; 8(x)
§1.7 闭区间上连续函数的基本性质 一、连续函数的和、差、积、商的连续性 定理1 (四则运算)若函数 和 在点 连续,则 f x( ) 0 g x( ) x (1) f x g x ( ) ( ) 在点 x0 连续; (2) ( ) ( ) 在点 连续; f x g x 0 x 0 ( ) , ( ( ) 0) ( ) f x g x g x (3) 在点 x0 连续;

二、反函数和复合函数的连续性 定理2如果函数y=f(x)在区间I.上单值、 单调增加(或单调减少)且连续,那么它的反函数 x=p(y)也在对应的区间1,={yly=fx),x∈Ix} 上单值、单调增加(或单调减少)且连续. 定理3设函数u=p(x),当x趋于x时的极限存 在且等于4,即1im0(x)=4,而函数y=f()在点u, 连续,那么复合函数y=f(x)】当x趋于x时的极限 存在且等于f),即1mf[p(x]=limf(0=)·
二、反函数和复合函数的连续性 定理2 如果函数 = 在区间 上单值、 单调增加(或单调减少)且连续,那么它的反函数 也在对应的区间 上单值、单调增加(或单调减少)且连续. y f (x) x I x = ( y) I y = y | y = f (x), x I x 定理3 设函数 ,当 趋于 时的极限存 在且等于 ,即 ,而函数 在点 连续,那么复合函数 当 趋于 时的极限 存在且等于 ,即 . u = (x) x 0 x 0 u 0 0 lim ( ) x x x u → = y = f (u) 0 u y = f(x) 0 x x 0 f u( ) ( ) ( ) 0 0 0 lim lim ( ) x x u u f x f u f u → → = =

例1求limsin(1-x2) x→1 例2 求极限: sinx sinx (1 (2 lim x>0 定理4 若函数u=p(x)在点x=x连续,且 p(x)=4,函数y=f(w)在点u=山,连续,则复合 函数y=f[p(x)】在点x=x也连续。 注意:定理4可以表示为: lim f(p(x))=f(lim p(x))=f(p(x))
例1 求 2 1 limsin(1 ) x x → − 例2 求极限: 0 sin sin (1) lim 2 ; (2) lim 2 x x x x → → x x − − 定理4 若函数 在点 连续,且 ,函数 在点 连续 ,则复合 函数 在点 也连续。 u x = ( ) 0 x x = 0 ( ) x u 0 0 = u u = y f x = ( ) 0 x x = y f u = ( ) 注意: 定理4 可以表示为: 0 0 0 lim ( ( )) (lim ( )) ( ( )) x x x x f x f x f x → → = =

三、初等函数的连续性 由上述讨论知: 三角函数 y=sinx,y=cosx,y=tanx,y=cotx 反三角函数 y=arcsin x,y=arccosx, y=arctanx,y=arccotx 指数函数 y=a',(a>0,a≠1) 对数函数 y=logx,(a>0,a≠1) 幂函数 y=x“ 基本初等函数在它们的定义域内都是连续的
三、初等函数的连续性 由上述讨论知: 三角函数 y x y x y x y x = = = = sin , cos , tan , cot 反三角函数 arcsin , arccos , arctan , cot y x y x y x y arc x = = = = 指数函数 , ( 0, 1) x y a a a = 对数函数 log , ( 0, 1) a y x a a = 幂函数 y x = 基本初等函数在它们的定义域内都是连续的

一切初等函数在其定义区间内都是连续的。 例3求极限 lim x2+n(2-x) x- 4arctan x sin x-sina 例4求极限 lim x-a 3 例5求极限1im(1+2x)snx
一切初等函数在其定义区间内都是连续的 。 例3 求极限 x x x x 4arctan ln( 2 ) lim 2 1 + − → 。 sin sin lim x a x a → x a − − 例4 求极限 。 例5 求极限 3 sin 0 lim(1 2 ) x x x → +

二、闭区间上连续函数的基本性质 定义设f为定义在数集I上的函数,若存在 x∈I使得对一切x∈I有f(xo)≥f(x(f(x)≤f(x) 则称f在1上有最大(最小)值,并称f(x)为f在 I上的最大(最小)值。 定理5(最大、最小值定理)若函数f(x)在闭区 间[a,b]上连续,则f(x)在[4,b]上有界且一定能取得它 的最大值和最小值
定义 设 为定义在数集 上的函数,若存在 使得对一切 有 则称 在 上有最大(最小)值,并称 为 在 上的最大(最小)值。 f I 0 x I x I 0 0 f x f x f x f x ( ) ( )( ( ) ( )) f I 0 f x( ) f I 二、闭区间上连续函数的基本性质 定理5 (最大、最小值定理)若函数 在闭区 间[a, b]上连续,则 在 [a, b] 上有界且一定能取得它 的最大值和最小值。 f x( ) f x( )
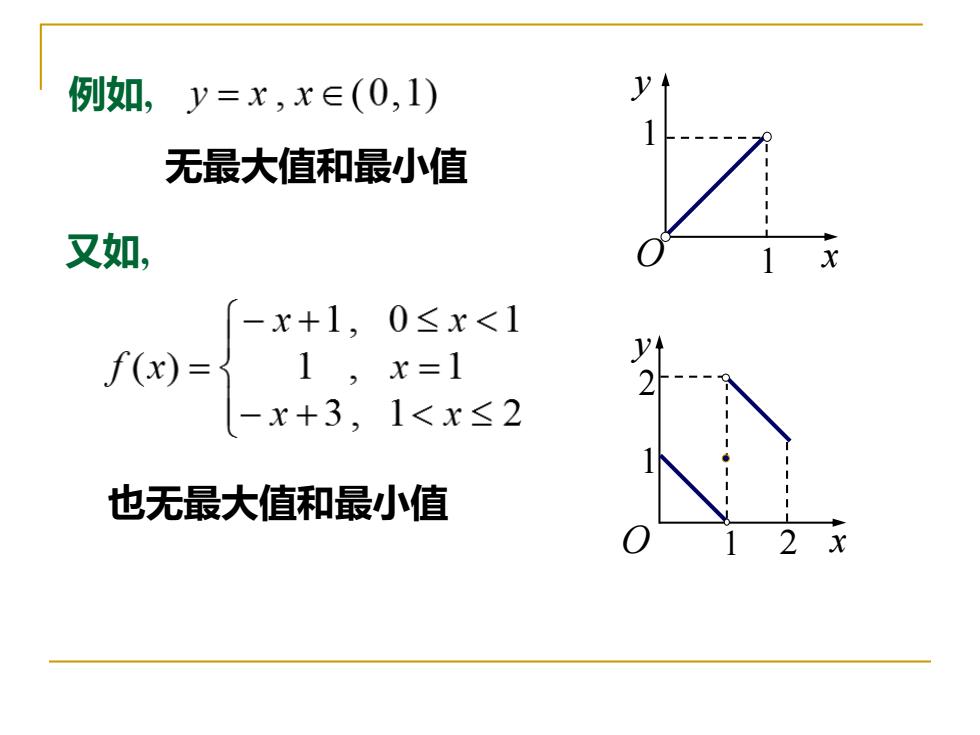
例如,y=x,x∈(0,1) 无最大值和最小值 又如, -x+1,0≤x<1 f(x)={ 1,x=1 -x+3,1<x≤2 也无最大值和最小值
例如, 无最大值和最小值 2 2 也无最大值和最小值 又如, x y 1 1 O x y O 1 1
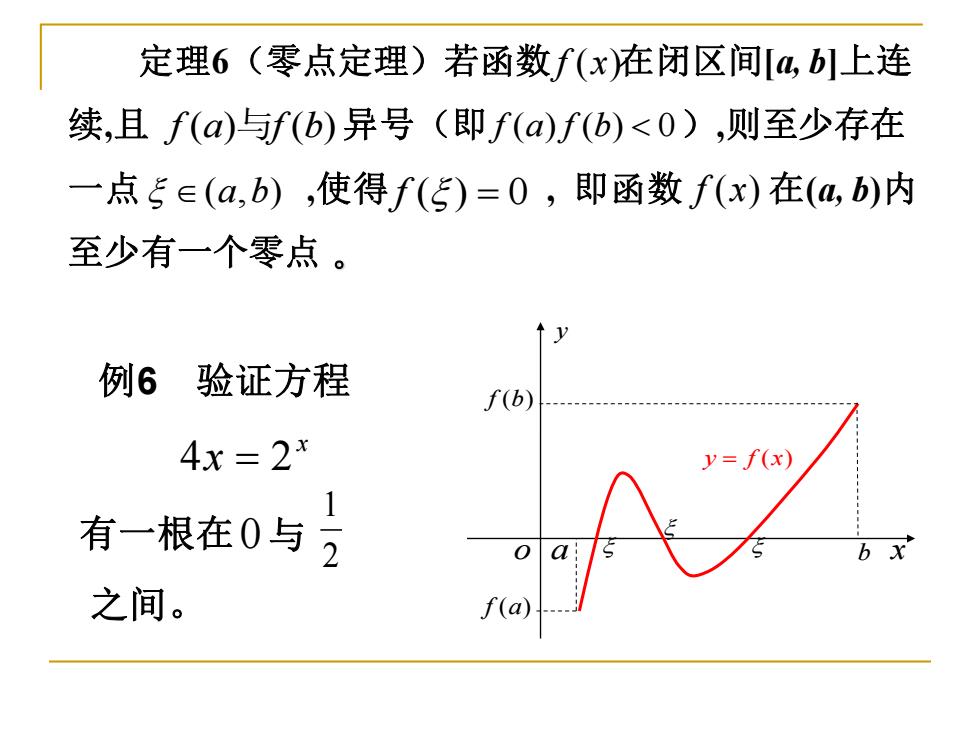
定理6(零点定理)若函数f(x在闭区间[4,b]上连 续,且f(a)与f(b)异号(即f(a)f(b)<0),则至少存在 一点5∈(a,b),使得f(5)=0,即函数f(x)在(a,b)内 至少有一个零点。 例6 验证方程 f(b) 4x=2 y=f(x) 有一根在0与 2 之间。 f(a
o a b x y f a( ) f b( ) y f x = ( ) 定理6(零点定理)若函数 在闭区间[a, b]上连 续,且 异号(即 ),则至少存在 一点 ,使得 , 即函数 在(a, b)内 至少有一个零点 f a f b ( ) ( ) 与 f a f b ( ) ( ) 0 ( , ) a b f ( ) 0 = 。 f x( ) f x( ) x 4x = 2 0 2 1 例6 验证方程 有一根在 与 之间
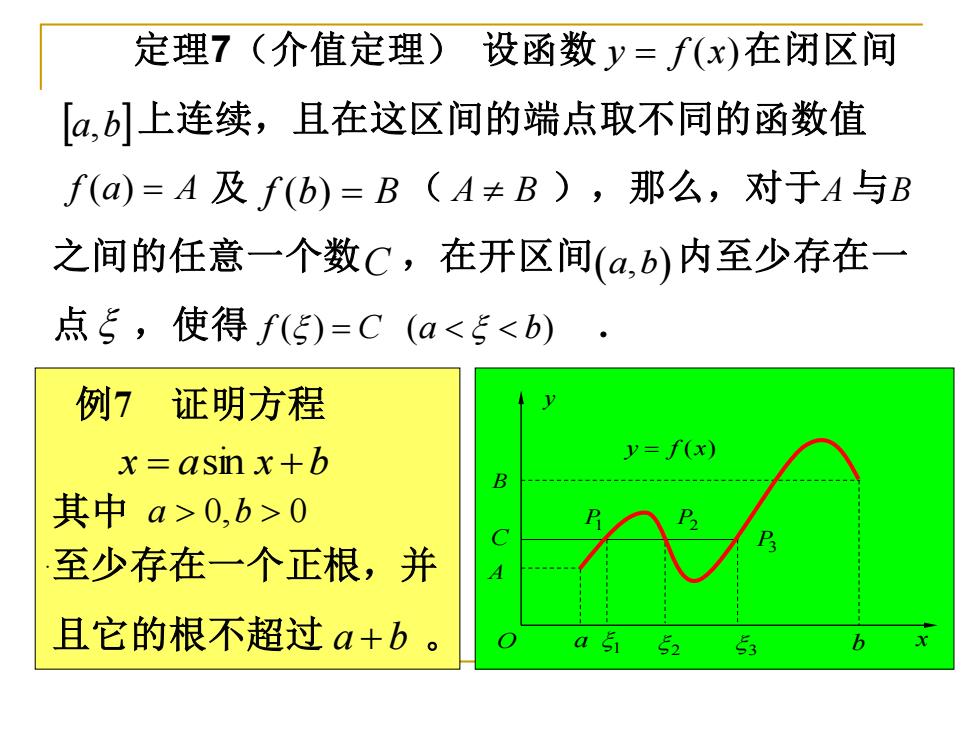
定理7(介值定理)设函数y=f(x)在闭区间 [4,b]上连续,且在这区间的端点取不同的函数值 f(a)=A及f(b)=B(A≠B),那么,对于A与B 之间的任意一个数C,在开区间(a,b)内至少存在一 点5,使得f(5)=C(a0,b>0 至少存在一个正根,并 且它的根不超过a+b a s 52 53 b
定理7(介值定理) 设函数 在闭区间 上连续,且在这区间的端点取不同的函数值 及 ( ),那么,对于 与 之间的任意一个数 ,在开区间 内至少存在一 点 ,使得 . y = f (x) a,b f (a) = A f (b) = B A B A B C (a b, ) f C a b ( ) ( ) = y f x = ( ) A B C y O a b x 1 2 3 P1 P2 P3 x = asin x +b a 0,b 0 a + b 例7 证明方程 . 其中 至少存在一个正根,并 且它的根不超过