
第五节广义积分 积分限有限 常义积分 被积函数有界 推 广义积分(反常积分) 一、无穷限的广义积分 二、无界函数的广义积分
二、无界函数的广义积分 第五节 常义积分 积分限有限 被积函数有界 一、无穷限的广义积分 广义积分 (反常积分) 广义积分 推 广
§5.5广义积分 一、无穷限的广义积分 1 引例曲线y=2和直线x=1及x轴所围成的开 口曲边梯形的面积 可记作4-广产的 其含义可理解为 rb dx =lim b→+0∞
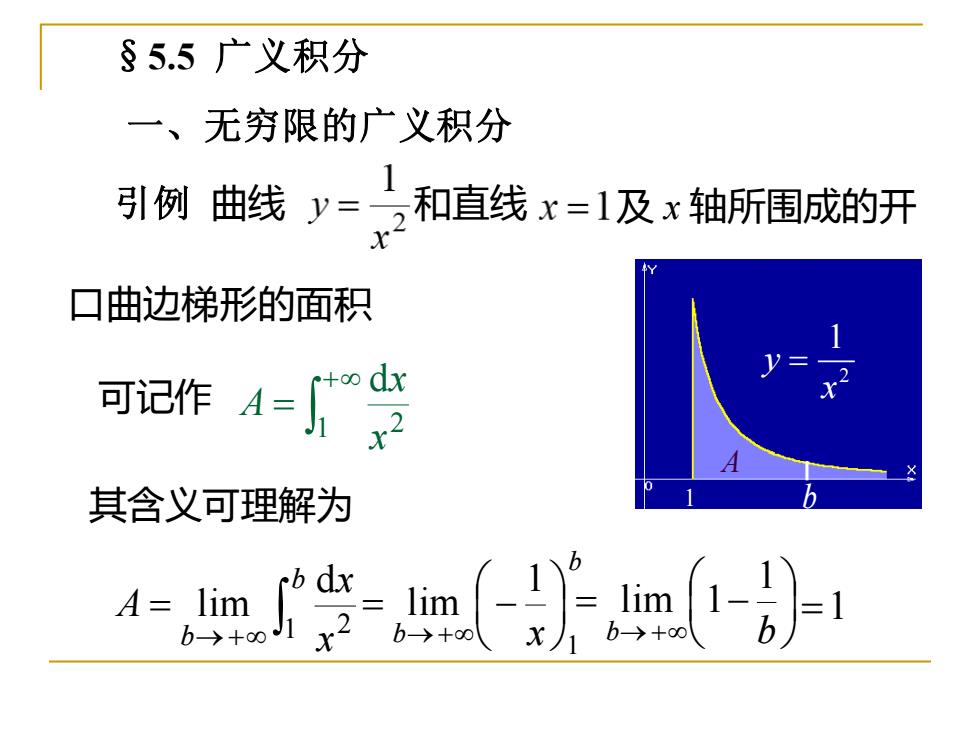
§5.5 广义积分 一、无穷限的广义积分 + = 1 2 d x x A 其含义可理解为 →+ = b b x x A 1 2 d lim 2 1 y x = A 1 b b b x 1 1 lim = − →+ = − b→+ b 1 lim 1 =1 引例 曲线 和直线 及 x 轴所围成的开 口曲边梯形的面积 可记作

定义1.设f(x)∈C[a,+o),取b>a,若 lim dx 存在,则称此极限为f(x)的无穷限广义积分,记作 d-no 这时称广义积分∫。f(x)dr收敛;如果上述极限不存在, 就称广义积分∫。f(x)dr发散 类似地,若f(x)∈C(-0,b],则定义 ∫fo)dr=1im&f)dr
定义1. 设 f (x)C[a, + ), 取b a, 若 存在 , 则称此极限为 f (x) 的无穷限广义积分, 记作 这时称广义积分 收敛 ; 如果上述极限不存在, 就称广义积分 发散 . 类似地 , 若 f (x)C(−, b], 则定义

若f(x)∈C(-o,+oo),则定义 d-limd+lim(d (c为任意取定的常数) 只要有一个极限不存在,就称∫f(x)d发散, 无穷限的广义积分也称为第一类广义积分 说明:上述定义中若出现0一0,并非不定型, 它表明该广义积分发散·
若 f (x)C(−, + ), 则定义 f x x c a a lim ( )d →− f x x b b c lim ( )d →+ + ( c 为任意取定的常数 ) 只要有一个极限不存在 , 就称 发散 . 无穷限的广义积分也称为第一类广义积分. 说明: 上述定义中若出现 − , 并非不定型 , 它表明该广义积分发散

若F(x)是f(x)的原函数,引入记号 F(+o)=lim F(x);F(-o)=lim F(x) x+00 则有类似牛-莱公式的计算表达式: /)dx=ra-r+o)-r@ f0=rFb)-(-四) [d=r(t2-o)-R-
引入记号 F( ) lim F(x) ; x→+ + = F( ) lim F(x) x→− − = 则有类似牛 – 莱公式的计算表达式 : f x x a ( )d + = F(x) = F(+) − F(a) f x x b ( )d − = F(x) = F(b) − F(−) f (x)dx + − = F(x) = F(+) − F(−)

例1计算广义积分了1+2 解小些 -+ =lim [arctanx+lim [aretanx -arctan c =π
例1. 计算广义积分 解: = o x y 2 1 1 x y + = a c b

思腾一X0国 +00 原积分发散! 注意:对广义积分,只有在收敛的条件下才能使用 “偶倍奇零”的性质否则会出现错误. 例2计算广义积分“te pidt(p>0). p 0 1
思考: 分析: 原积分发散 ! 注意: 对广义积分, 只有在收敛的条件下才能使用 “偶倍奇零”的性质否则会出现错误 , . 例2 计算广义积分 解: pt e p t − 原式 = − + − + 0 d 1 e t p pt pt e p − = − 2 1 2 1 p =

证明第-美p积分当P1时收敬 p≤1时发散. 证:当p=1时有 =[Inlx]=+0 当p≠1时有 。{ p1 D-1 al-p 因此,当p>1时,广义积分收敛,其值为 当p≤1时,广义积分发散
例2. 证明第一类 p 积分 证:当 p =1 时有 + = a ln x = + − + − = a p p x 1 1 当 p ≠ 1 时有 p 1 p 1 , 1 1 − − p a p 当 p >1 时收敛 ; p≤1时发散 . + , 因此, 当 p >1 时, 广义积分收敛 , 其值为 ; 1 1 − − p a p 当 p≤1 时, 广义积分发散

二、无界函数的广义积分 写所声线y= 与x轴,y轴和直线x=1所围成的 开口曲边梯形的面积可记作 4- 其含义可理解为 A=lim dx s0+Jε/元=1im2VeA ;6→0 =lim2(1-√ε)=2 8-→01
二、无界函数的广义积分 引例:曲线 与 x 轴, y 轴和直线 所围成的 开口曲边梯形的面积 可记作 其含义可理解为 + → = 1 0 d lim x x A 1 lim 2 0 x → + = lim 2(1 ) 0 = − → + = 2 1 y x = 0 A x y

定义2.设f(x)∈C(a,b],而在点a的右邻域内无界, 取e>0,若极限1imf(x)dr存在,则称此极限为函 8)0 a+8 数f(x)在[a,b]上的广义积分,记作 dr-imds 8)0+ 这时称广义积分∫f(x)dr收敛;如果上述极限不存在, 就称广义积分∫”f()dr发散. 类似地,若f(x)∈C[a,b),而在b的左邻域内无界, 则定义 )dw-limd
定义2. 设 f (x)C(a, b], 而在点 a 的右邻域内无界, 存在 , 这时称广义积分 收敛 ; 如果上述极限不存在, 就称广义积分 发散 . 类似地 , 若 f (x)C[a, b), 而在 b 的左邻域内无界, 若极限 数 f (x) 在 [a , b] 上的广义积分, 记作 则定义 则称此极限为函