
上次课内容复习: 改错 π(4+7π)》 1.二元函数全微分的定义; 2.二元函数全微分存在的必要条件; 3.二元函数全微分存在的充分条件; 4.函数在一点极限存在、连续、偏导数存在、 可微、偏导数连续之间的关系
上次课内容复习: 1. 二元函数全微分的定义; 2. 二元函数全微分存在的必要条件; 3. 二元函数全微分存在的充分条件; 4. 函数在一点极限存在、连续、偏导数存在、 可微、偏导数连续之间的关系。 2 (4 7 ) 8 改错 ( + )

二、全微分在近似计算中的应用 如果二元函数z=f(x,y)的两个偏导数∫,(x,y)、 f,(x,y)在点(x,y)连续,并且当△x,|Ay|都较小时, 全增量可近似地用全微分来代替,即 Az≈d=f(x,y)△x+f(x,y)△y 上式也可写为: f(x+△x,y+△y)≈f(x,y)+fx(x,y)△x+f(x,y)△W 利用上式可以对二元函数进行近似计算
二、全微分在近似计算中的应用 如果二元函数 的两个偏导数 、 在点 连续,并且当 , 都较小时, 全增量可近似地用全微分来代替,即 上式也可写为: 利用上式可以对二元函数进行近似计算。 z = f (x, y) f (x, y) x f (x, y) y (x, y) | x | | y | z z f x y x f x y y d = x ( , ) + y ( , ) f x x y y f x y f x y x f x y y ( + , + ) ( , ) + x ( , ) + y ( , )

例5计算(1.02)2.04的近似值. 例6圆柱体形变时,底半径由30cm增大到30.1cm 高由60cm减少到59.5cm。求此圆柱体体积变化的 近似值
例5 计算 2.04 (1.02) 的近似值. 例6 圆柱体形变时,底半径由 增大到 高由 减少到 。求此圆柱体体积变化的 30cm 30.1cm 60cm 59.5cm 近似值

§7.4多元复合函数的求导法则 一元函数有关概念的复习。 定理1如果函数u=p(x),v=(x),都在点x可 导,函数z=f(u,v)在对应点(u,v)具有连续偏导数 则复合函数z=f[p(x),(x】在点x可导,且 dzdz du oz dv dx Ou dx Ov dx 例1设z=e2w-vu=nxv=sinx dz 求: dx
定理1 如果函数 , ,都在点 可 导,函数 在对应点 具有连续偏导数 则复合函数 在点 可导,且 u = (x) v = (x) x z = f (u,v) (u,v) z = f [(x),(x)] x x v v z x u u z x z d d d d d d + = §7.4 多元复合函数的求导法则 一元函数有关概念的复习。 例1 设 u v z − = 2 e u = ln x v = sin x 求: x z d d
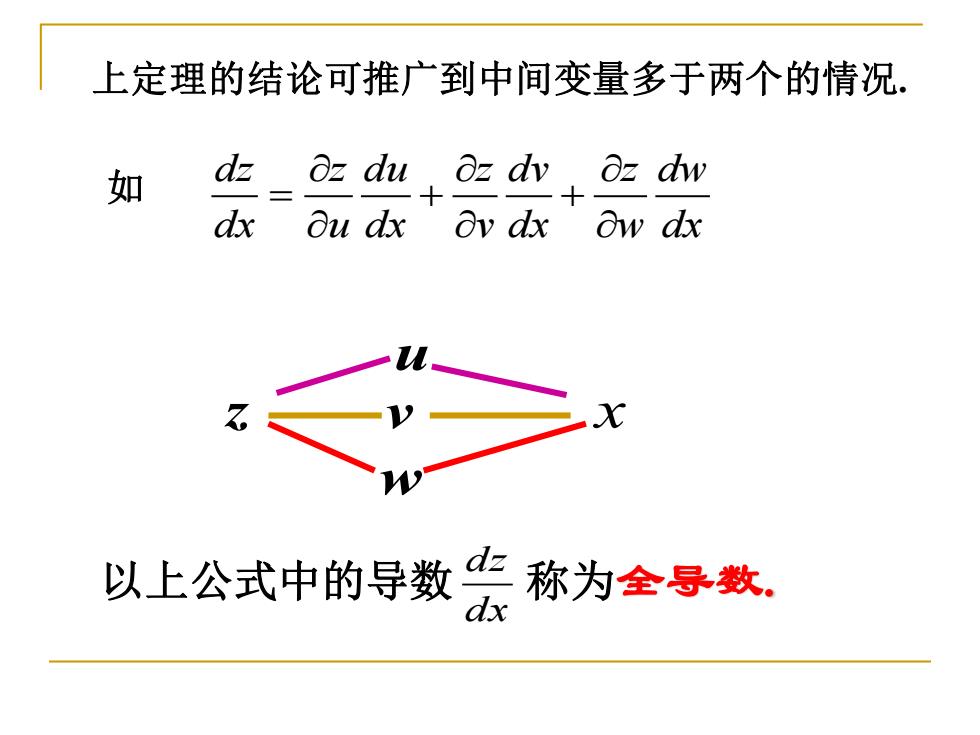
上定理的结论可推广到中间变量多于两个的情况. 如 dz Oz du oz dv oz dw dx Ou dx Ov dx Ow dx 以上公式中的导数你称为全导数
上定理的结论可推广到中间变量多于两个的情况. 如 dz z du z dv z dw dx u dx v dx w dx = + + z u v w x 以上公式中的导数 称为全导数. dz dx

定理2如果函数M=p(x,y),v=(x,y)都在点(x,y) 存在对x、y的偏导数,函数z=f(u,)在对应点(u,v) 具有连续偏导数,则复合函数z=[p(x,y),(x,y川在点 (x,)的两个偏导数、都存在,且 Ox ay OzOz Ou Oz Ov ① ax au ax av ax 0z0z Ou Oz Ov 2) ay Ou ay ov ay 上式称为复合函数求导的链式法测
定理2 如果函数 , 都在点 存在对 、 的偏导数,函数 在对应点 具有连续偏导数,则复合函数 在点 的两个偏导数 、 都存在,且 u = (x, y) v x y = ( , ) (x, y) x y z = f (u,v) (u,v) z = f [(x, y),(x, y)] (x, y) x z y z 1 z z u z v x u x v x = + () 2 z z u z v y u y v y = + () 上式称为复合函数求导的链式法则

链式法则如图示 多元复合函数的求导法则简言之即: “分道相加,连线相乘
链式法则如图示 z u v x y 多元复合函数的求导法则简言之即: “分道相加,连线相乘

例2 z=u2v-uv2 v=xsin y u=xcosy 求: 0z 8z 8x ’y 解:正_0.0+产.=(2w-2)c0sy+(ar2-2)siny Ox au ax dy Ox =(2x2cos ysiny-x2 sin2 y)cosy+ (x2 cos2 y-2x2sinycosy)siny =3x2sin ycos y(cos y-siny) OzOz Ou 8z Ov y ou ay ov ay =x3(sin3 y+cos3y-sin ysin2y-cos ysin2y)
, 例2 设 求: 2 2 z = u v − uv v = x sin y u = x cos y x z y z 解: x v v z x u u z x z + = (2uv v )cos y (u 2uv)sin y 2 2 = − + − 2 2 2 2 2 2 (2 cos sin sin )cos ( cos 2 sin cos )sin x y y x y y x y x y y y = − + − 2 = − 3 sin cos (cos sin ) x y y y y y v v z y u u z y z + = 3 3 3 = + − − x y y y y y y (sin cos sin sin 2 cos sin 2 )

例3 设 u=f(x,y,=)=e=y2 sin x 求: Bu Bu d Ov 例4设 =f(ysin x.,e) 求: 0z 0z 例5 已知:=f0+x+,且f具有二阶连续偏 导数,求: 62zz Ox2'Oxoy
2 2 2 e 例 x + y +z 3 设 , 求: , u = f (x, y,z) = z y sin x 2 = x u y u 。 例4 设 , ( sin , , x y z = f y x x+ y e ) 求: x z y z . 例5 已知 ,且 具有二阶连续偏 , ) 1 , 1 ( y x x z = f y + + f 2 2 x z x y z 2 导数,求:

设z=f(u,v),如果u,是自变量,则全微分为: dz +产 如果,是中间变量,且又是自变量x,的可微函数,即 u=p(x,y),v=V(x,y),==f[o(x,y),w(x,y) 则全微分为: dz k+ y o2 ou 8Ovdx+ d ou ozov dy Ox y Ou ax av &x) ou ay ov ay v &x du+ov Bu 上式称为多元函数的一阶微分形式不变性
z f u v u v ( , ), , z z dz du dv u v = = + 设 如果 是自变量,则全微分为: 上式称为多元函数的一阶微分形式不变性。 , , ( , ), ( , ), ( , ), ( , ) u v x y u x y v x y z f x y x y = = = 如果 是中间变量,且又是自变量 的可微函数,即 z z dz dx dy x y = + 则全微分为: z u z v z u z v dx dy u x v x u y v y = + + + z u u z v v dx dy dx dy u x y v x y = + + + z z du dv u v = +