
第七章 多元函数微分学 我们前面讨论的函数只含有一个自变量,这种函 数称为一元函数但在许多实际问题中,常常会遇到依 赖于多个自变量的函数,即多元函数.例如,某种商品的 市场需求量不仅与其市场价格有关,而且与消费者的 收入等因素有关,即决定该商品需求量的因素不止一 个 本章将讨论多元函数微分学及其应用
第七章 多元函数微分学 我们前面讨论的函数只含有一个自变量,这种函 数称为一元函数.但在许多实际问题中,常常会遇到依 赖于多个自变量的函数,即多元函数.例如,某种商品的 市场需求量不仅与其市场价格有关,而且与消费者的 收入等因素有关,即决定该商品需求量的因素不止一 个. 本章将讨论多元函数微分学及其应用

§7.1多元函数的基本概念 一、平面点集 在平面直角坐标系中,建立了坐标平面上点与一 对有序数(x,y)的一一对应的关系。 坐标平面上满足某种条件P的点的集合,称为平 面点集,记作:E={(x,)水(x,y)满足条件P 例1全平面上的点集: R2={(x,y)-0<x<+o,-0<y<+∞} ()
一、平面点集 在平面直角坐标系中,建立了坐标平面上点与一 对有序数 ( , ) x y 的一一对应的关系。 坐标平面上满足某种条件 的点的集合,称为平 面点集,记作: P E x y x y P = ( , ) ( , )满足条件 例1 全平面上的点集 : 2 R x y x y = − + − + ( , ) , (1) §7.1 多元函数的基本概念

例2以原点为中心,r为半径的圆 的内部的所C={x,x+y<(②- 有点的集合: 特别地,平面点集: {(x,y)x-x)2+(y-)2<82} 称为以P(x)为中心的6, 邻域记为U(P,6)。 {x,y)l0<(x-x)2+(y-%)2<82} 称为空心邻域,记为U°(P;δ)
特别地,平面点集: 2 2 2 0 0 ( , ) ( ) ( ) x y x x y y − + − 称为以 P x y 0 0 0 ( , ) 为中心的 , x y o P0 2 2 2 0 0 ( , ) 0 ( ) ( ) x y x x y y − + − 称为空心邻域, x y o P0 例2 以原点为中心,r 为半径的圆 的内部的所 有点的集合: 2 2 C x y x y r = + ( , ) (2) y o x r 0 邻域记为 U P( ; ) 。 0 0 记为 U P( ; )
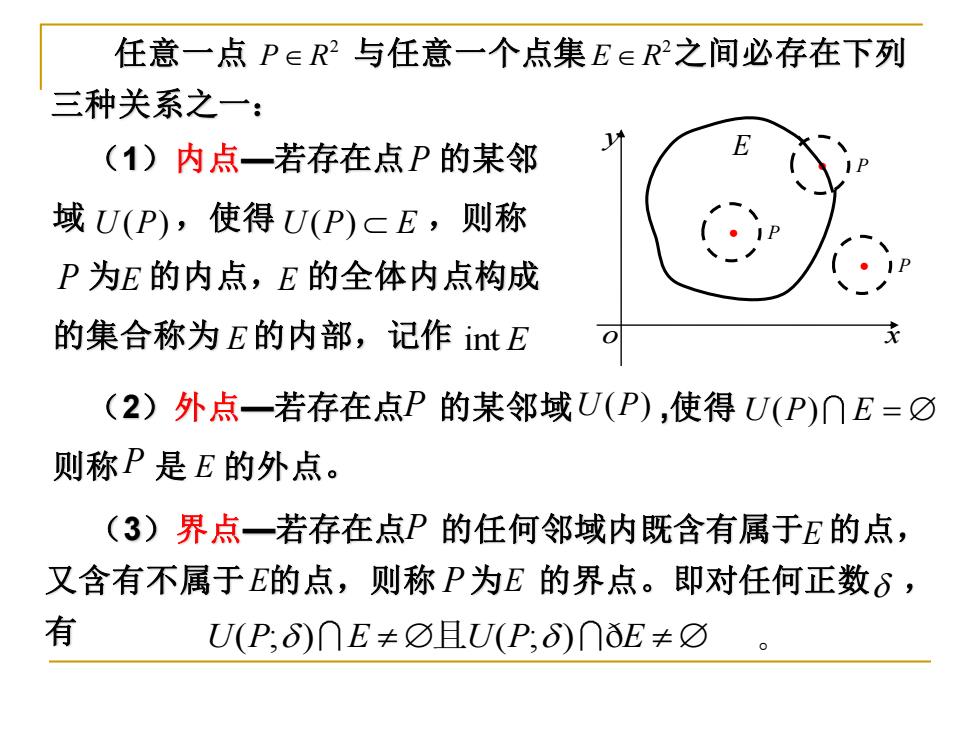
任意一点P∈R2与任意一个点集E∈R2之间必存在下列 三种关系之一: (1)内点一若存在点P的某邻 域U(P),使得U(P)cE,则称 P为E的内点,E的全体内点构成 的集合称为E的内部,记作intE (2)外点一若存在点P的某邻域U(P),使得U(P)∩E=O 则称P是E的外点。 (3)界点一若存在点P的任何邻域内既含有属于E的点, 又含有不属于E的点,则称P为E的界点。即对任何正数δ, 有 U(P,6)∩E≠☑且U(P,6)∩ǒE≠☑
任意一点 与任意一个点集 之间必存在下列 三种关系之一: 2 P R 2 E R y o x ( E 1)内点—若存在点 的某邻 域 ,使得 ,则称 为 的内点, 的全体内点构成 的集合称为 的内部,记作 P U P( ) U P E ( ) P E E E int E • P (2)外点—若存在点 的某邻域 ,使得 则称 是 的外点。 U P( ) U P E ( ) = P E P • P • P (3)界点—若存在点 的任何邻域内既含有属于 的点, 又含有不属于 的点,则称 为 的界点。即对任何正数 , 有 U P E U P E ( ; ) ( ; ) 且 ð P P E E E

说明:E的边界点可能属于E,也可能不属于E。 以下按在点P的近旁是否密集着E中的无穷多个点而构 成另一类关系 (1)聚点一若在点P的任何空心邻域内都含有E中的 点,则称P是E的聚点。聚点可能属于E,也可能不属于E (2)孤立点一若点P属于E,但不是E的聚点,即存在 某一个正数δ使得U°(P,6)∩E=⑦,则称P为E的孤立 点。 例3讨论平面点集 D={x,yl≤x2+y2<4}
说明: E 的边界点可能属于 E ,也可能不属于 E 。 以下按在点 的近旁是否密集着 中的无穷多个点而构 成另一类关系: P E (1)聚点—若在点 的任何空心邻域内都含有 中的 点,则称 是 的聚点。聚点可能属于 ,也可能不属于 P E P E E E (2)孤立点—若点 属于 ,但不是 的聚点,即存在 某一个正数 ,使得 ,则称 为 的孤立 点。 P E E ( ; ) o U P E = P E 例3 讨论平面点集 2 2 D x y x y = + ( , ) 4 1 x y o D

某些重要平面点集的定义 开集一若平面点集所属的每一个点都是E的内点,则称E 为开集。 闭集一若平面点集E的所有聚点都属于E,则称E为闭集, 若点集没有聚点,这时也称为闭集。 开区域一若非空开集E具有连通性,则称E为开域。 闭区域一开域连同其边界所组成的点集称为闭域。 区域一开区域、闭区域,或者开区域连同其一部分界点 所成的点集,统称为区域
开集—若平面点集所属的每一个点都是 的内点,则称 为开集。 E E 闭集—若平面点集 的所有聚点都属于 ,则称 为闭集, 若点集 没有聚点,这时也称 为闭集。 E E E E E 开区域—若非空开集 E 具有连通性 ,则称 E 为开域。 某些重要平面点集的定义 闭区域—开域连同其边界所组成的点集称为闭域。 区域—开区域、闭区域,或者开区域连同其一部分界点 所成的点集,统称为区域
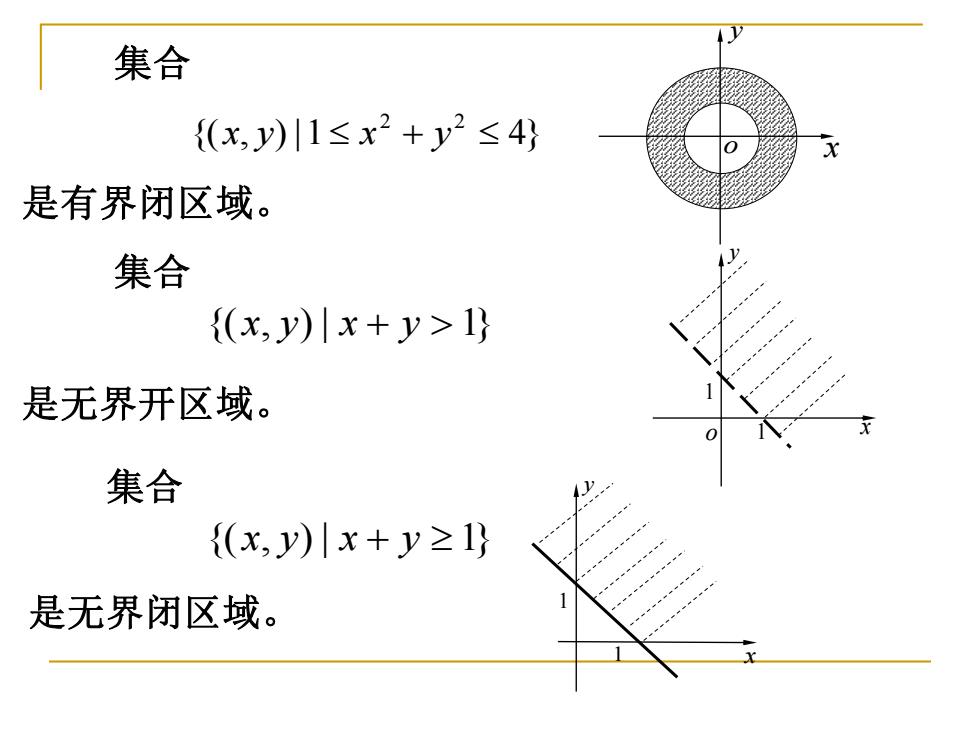
集合 {(x,y)川1≤x2+y2≤4} 是有界闭区域。 集合 出 (x,y)川x+y>1} e-m 是无界开区域。 集合 {(x,y)川x+y≥1 是无界闭区域
{( , ) |1 4} 2 2 x y x + y 是有界闭区域。 集合 {( x, y) | x + y 1} 是无界开区域。 集合 {( x, y) | x + y 1} 是无界闭区域。 集合 y o x y x 1 o 1 y x 1 1

二、多元函数的概念 例4设银行存款利率为r,将10000元存入银行,不 计复利,则t年后的本利和为: M=10000(1+r)' 当和的值取定后,则的对应值也随之确定. 例5圆柱体的侧面积S,底半径和高h之间具有 关系: S=2πrh 当r、h在集合{(r,h)川r>0,h>0;内取定一对值(r,h) 时,S的对应值就随之确定
二、 多元函数的概念 例4 设银行存款利率为r,将10000元存入银行,不 计复利,则t 年后的本利和为: 当r和t的值取定后,则的对应值也随之确定. t M =10000 (1+ r) 例5 圆柱体的侧面积S,底半径r和高h之间具有 关系: 当r、h在集合 内取定一对值 时, S的对应值就随之确定. S = 2 r h {(r,h) | r 0,h 0} (r,h)

例6一定量的理想气体的压强p、体积和绝对 温度T之间具有关系 RT p= 其中R为常数.当V、T在集合(V,T)1V>0,T>To}内取 定一对值(W,T)时,p的对应值就随之确定
例6 一定量的理想气体的压强 p、体积V和绝对 温度T之间具有关系 其中R为常数.当V、T在集合 内取 定一对值 时, 的对应值就随之确定. RT p V = {( , ) | 0, } V T V T T0 (V ,T ) p

多元函数的定义 定义1设D是平面上的一个点集,对于任意一 点P(x,y)∈D,变量z按照一定的法则总有确定的值 与之对应,则称z是变量x,y的二元函数,记作 z=f(x,y),(或z=f(P) 其中点集D称为该函数的定义域,x,y称为自变量, z称为因变量。 类似地可以定义三元函数u=f(x,y,z)以及三元 以上的函数,二元和二元以上的函数统称为多元函数
多元函数的定义 定义1 设D是平面上的一个点集,对于任意一 点 ,变量z按照一定的法则总有确定的值 与之对应,则称z是变量 的二元函数,记作 其中点集D称为该函数的定义域, 称为自变量, z 称为因变量。 P x y D ( , ) x y, z = f (x, y) ,(或 z = f (P) ) x y, 类似地可以定义三元函数 u = f (x, y,z) 以及三元 以上的函数,二元和二元以上的函数统称为多元函数