
第一章 第十节闭区间上连续函数的性质 所谓函数f(x)在闭区间[a,b]上连续,是指 f(x)在开区间(a,b)内连续,且在左端,点a右连续, 在右端,点b左连续. 闭区间上的连续函数具有一些重要的性质,在 几何直观上是十分明显的,但严格证明比较困难, 下面我们以定理的形式给出这些性质,其证明均已 略去 2009年7月3日星期五 上页 下页 返回 结束
2009年7月3日星期五 1 上页 下页 返回 结束 第十节 闭区间上连续函数的性质 第一章 所谓函数 f ( ) x 在闭区间 [,] a b 上连续,是指 f ( ) x 在开区间(,) a b 内连续,且在左端点 a 右连续, 在右端点 b 左连续. 闭区间上的连续函数具有一些重要的性质, 在 几何直观上是十分明显的,但严格证明比较困难, 下面我们以定理的形式给出这些性质,其证明均 已 略去.

一、有界性与最大值最小值定理 定理1在闭区间上连续的函数在该区间上有界且 一定能取得它的最大值和最小值 即:设f(x)∈C[a,b],则351,52∈[a,b],使 f(s)=min f(x) yy=f(x) a≤x≤b f(2)=max f(x) a≤x≤b 0a5152bx 注意:若函数在开区间上连续,或在闭区间内有间断 点,结论不一定成立 2009年7月3日星期五 2 上页 下页 返回 结束
2009年7月3日星期五 2 上页 下页 返回 结束 一、有界性与最大值最小值定理 定理 1 在闭区间上连续的 函数在该区间上有界 且 一定能取得它的最大值和最小值. 即: 设 baCx ,],[)( 注意 : 若函数在开区间上连续, 结论不一定成立 . f ∈ o x y a b = xfy )( ξ 1 ξ 2 则 ,],[, 21 ∃ ξ ξ ∈ ba 使 )(min)( 1 f f x ≤≤ bxa ξ = )(max)( 2 f f x ≤≤ bxa ξ = 或在闭区间内有间断 点
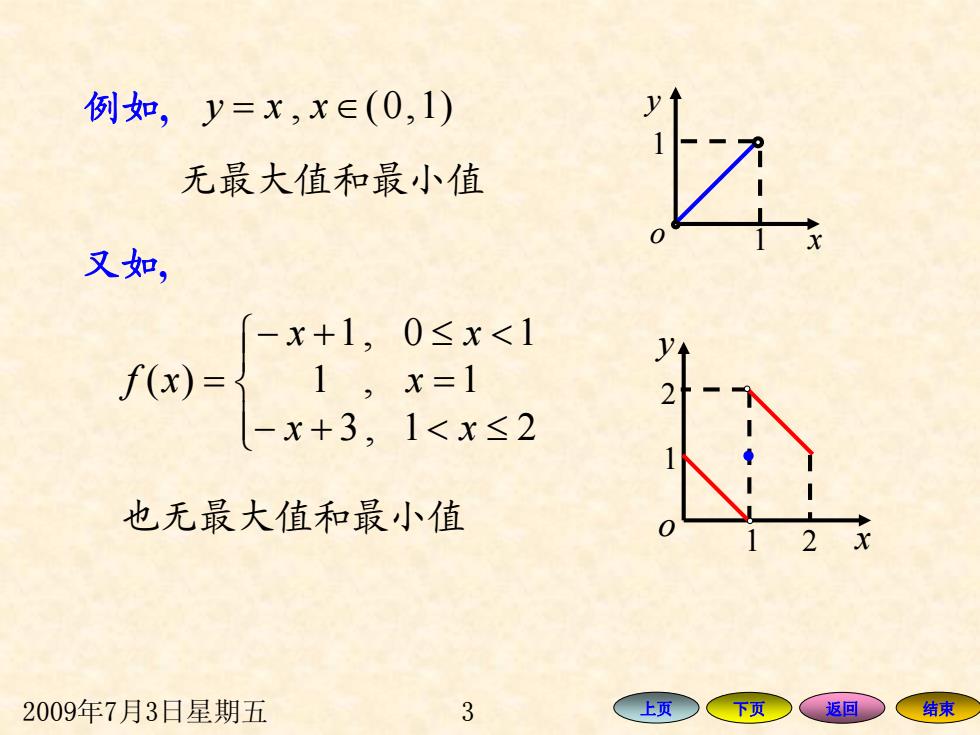
例如,y=x,x∈(0,1) 无最大值和最小值 又如, -x+1,0≤x<1 f(x)=了 1,x=1 -x+3, 1<x≤2 也无最大值和最小值 2 2009年7月3日星期五 3 上页 下页 返回 结束
2009年7月3日星期五 3 上页 下页 返回 结束 例如 , y = xx ∈ )1,0(, 无最大值和最小值 o x y 1 1 ⎪⎩ ⎪ ⎨ ⎧ ≤<+− = − + ≤ < = 21,3 1,1 10,1 )( xx x xx xf x o y 1 1 2 2 也无最大值和最小值 又如

二、零,点定理和介值定理 定义如果x,使得f(x)=0,就称x,为函数 f(x)的零点(或称x。为方程f(x)=0的根, 定理2(零点定理)f(x)∈C[a,b],'y=f(x以 且f(a)f(b)<0◆至少有一点 0 5∈(a,b),使f(5)=0.(证明略) 定理3(介值定理)设f(x)∈C[a,b],且f(a)=A, f(b)=B,A≠B,则对A与B之间的任一数C,至少有 一点5∈(a,b),使f(5)=C.(可利用零点定理证明) 2009年7月3日星期五 4 C上页 下页 返回 结束
2009年7月3日星期五 4 上页 下页 返回 结束 二、零点定理和介值定理 定义 如果 0 x 使得 0 f x()0 = ,就称 0 x 为 函 数 f ( ) x 的零点(或称 0 x 为方程 f x() 0 = 的 根). 定理2 ( 零点定理 ) f x ∈ C ba ,],[)( 至少有一点 ξ ∈ ba ,),( 且 使 x y o a b y = f x)( ξ f ξ = .0)( f a f b < 0)()( ( 证明略 ) 定理3 (介值定理 ) 设 f x ∈ C ba ,],[)( 且 f = Aa ,)( f b = B A ≠ B ,)( 则对 A 与 B 之间的任一数 C , 一点 ξ ∈ ba ,),( 使 f ξ = C.)( 至少有 ( 可利用零点定理证明 )

例1证明方程x3-4x2+1=0在区间(0,1)内至少有 一个根.(补充题) 证:显然f(x)=x3-4x2+1∈C[0,1],又 f(0)=1>0,f(1)=-20, 则(2,1)内必有方程的根; 取[,]的中点x=,f()<0, 则(兮,)内必有方程的根;. 可用此法求近似根。 2009年7月3日星期五 5 上页 下页 返回 结束
2009年7月3日星期五 5 上页 下页 返回 结束 014 23 x − x + = 一个根 . ,]1,0[14)( 23 证 : 显然 ∈+−= Cxxxf 又 f = > ,01)0( f −= )1,( 内必有方程的根 ; 2 1 取 ]1,[2 1 的中点 , 4 3 x = ,0)(4 3 f < ),( 内必有方程的根 ; 4 3 2 1 " 可用此法求近似根 . 二分法 4 3 2 0 1 1 x + − + − 在区间 )1,0( 取 ]1,0[ 的中点 则 内至少有 则 例1 证明方程 (补充题)

例2设f(x)在[a,b]上连续,且恒为正,证明: 对任意的x1,x2∈(a,b),x10,.F(x1)F(x2)<0, 故由零点定理知,存在5∈(x1,x2),使F(5)=0,即 f(5)=Vf(x1)f(x2) 2009年7月3日星期五 6 上页 下页 返回 结束
2009年7月3日星期五 6 上页 下页 返回 结束 0)()()( 21 2 ξ − xfxff = xf )( ba ],[ 上连续 , 且恒为正 , 对任意的 ,),(, 21 21 xxbaxx 在 ∈ ,0)( ,0)()( ∴ F x F x21 < 故由零点定理知 , 存在 ,),( 21 ξ ∈ xx F ξ = ,0)( 即 .)()()( 21 ξ = xfxff 当 )()( 1 2 = xfxf 时 , 取 1 ξ = x 或 2 ξ = x , 则有 )()()( 21 ξ = xfxff 例2 设 证明 : (补充题)

内容小结 设f(x)∈C[a,b],则 1.f(x)在[a,b]上有界; 2.f(x)在[a,b]上达到最大值与最小值; 3.当f(a)f(b)<0时,必存在5∈(a,b),使f(5)=0; 4.f(x)在[a,b]上可取最大与最小值之间的任何值. 2009年7月3日星期五 7 上页 下页 返回。 结束
2009年7月3日星期五 7 上页 下页 返回 结束 内容小结 设 f ∈ baCx ,],[)( 则 xf )(.1 在 上达到最大值与最小值 ; 3. 当 f a f b < 0)()( 时 , 必存在 ξ ∈ ba ,),( 使 f ( ) 0; ξ = ba ],[ 上有界 ; xf )(.2 在 ba ],[ 4. ( ) f x 在 ba ],[ 上可取最大与最小值之间的任何值

课后练习 习题1-10 245 复习题A、B 思考与练习 1.任给一张面积为A的纸片(如图),证明必可将它 一刀剪为面积相等的两片. y 提示:建立坐标系如图. S( 则面积函数S(O)∈C[a,B] 因S(x)=0,S(B)=A Bn 故由介值定理可知:30∈(a,B),使S(0) A 2009年7月3日星期五 8 上页 下页 返回 结束
2009年7月3日星期五 8 上页 下页 返回 结束 课后练习 习 题 1-10 2 4 5 复习题 A 、 B 思考与练习 1. 任给一张面积为 A 的纸片 (如图), 证明必可将它 一刀剪为面积相等的两片 . 提示 : 建立坐标系如图 . x o y β α θ 则面积函数 θ ∈CS α β ],[)( 因 S α = ,0)( β )( = AS 故由介值定理可知 : ,),( ∃ θ 0 ∈ α β . 2 )( 0 A 使 S θ = S θ )(

2.证明x=ex-3+1至少有一个不超过4的正根 证:令f(x)=x-ex-3-1 显然f(x)在闭区间[0,4]上连续,且 f(0)=-e3-10 根据零点定理,在开区间(0,4)内至少存在一点 5∈(0,4),使f(5)=0,原命题得证. 2009年7月3日星期五 9 上页今 下页→ 返回> 结束
2009年7月3日星期五 9 上页 下页 返回 结束 xf )( 在闭区间 [ ]上连续,4,0 3 e 1 x x − = + 至少有一个不超过 4 的正根 . 证:令 3 () e 1 x fx x − 证明 = − − 且 f )0( = 3 e 1 − − − f )4( = 4 3 4e 1 − − − 根据零点定理 , ξ ∈ ,)4,0( 使 f ξ = ,0)( 原命题得证 . 在开区间 )4,0( 内至少存在一点 显然 2

3.f(x)∈C[0,2a则,f(0)=f(2a),证明至少存在一,点 5∈[0,a],使f(5)=f(5+a) 提示:令p(x)=f(x+a)-f(x), 则p(x)∈C[0,a], 易证p(0)p(a)≤0 2009年7月3日星期五 10 (上页下页)返回 结束
2009年7月3日星期五 10 上页 下页 返回 结束 f x ∈ C a ,]2,0[)( f = f a ,)2()0( 证明至少存在一点 ξ ∈ a ,],0[ 使 f ξ = f ξ + a .)()( 提示 : 令 ϕ x = f + ax − f x ,)()()( 则 ϕ x ∈ C a ,],0[)( 易证 ϕ ϕ a ≤ 0)()0( 3