
第一章 第、节品数的连续性写间断点 Continuity and Discontinuity of Function) 一、问题的提出 二、函数的连续性 三、函数的间断点 四、小结与思考题 2009年7月3日星期五 1 目录○ 上页 下页 、返回
2009年7月3日星期五 1 目录 上页 下页 返回 第 八节 函数的连续性与间断点 第一章 (Continuity and Discontinuity of Function ) 三、函数的间断点 二、函数的连续性 一、问题的提出 四、小结与思考题
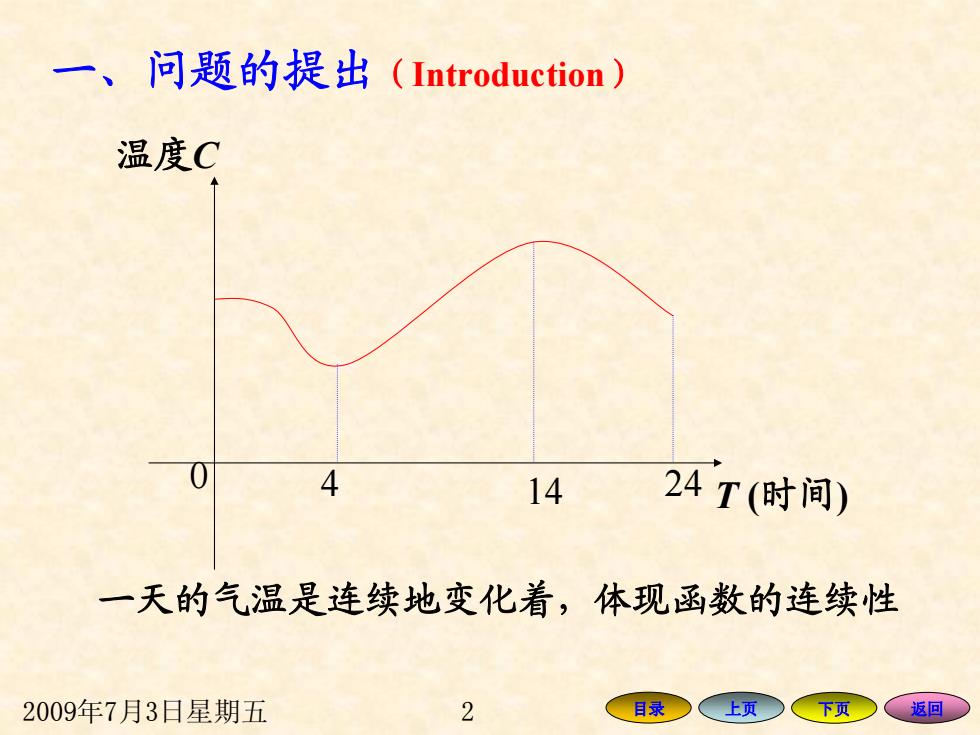
一、问题的提出(Introduction) 温度C 14 24T(时间) 一天的气温是连续地变化着,体现函数的连续性 2009年7月3日星期五 2 目录 (上页 下页 、返回
2009年7月3日星期五 2 目录 上页 下页 返回 一、问题的提出 (Introduction ) 0 T (时间 ) 温度 C 4 14 24 一天的气温是连续地变化着,体现函数的连续性

二、函数的连续性(Continuity of Function) 1.函数的增量 设变量x从初值x变到终值x2,终值与初值的差x,-x 叫做变量x的增量,记作△x,即△x=x2-x· 显然,增量△x可以是正的,也可以是负的. △y=f(x2)-∫(x1)叫做函数值的增量. 一般地,设函数y=f(x)在,点x,的某一个邻域内是有定义的 当自变量x在这邻域内从x变到x,+△x时,函数值y相应 地从f(x)变到f(x。+△x),因此,函数y的对应增量为 Ay=f(x+△x)-f(x) 2009年7月3日星期五 3 目录 上页 下页 返回
2009年7月3日星期五 3 目录 上页 下页 返回 二、函数的连续性 (Continuity of Function ) 1.函数的增量 设变量 x 从初值 1 x 变到终值 2 x ,终值与初值的差 2 1 x − x 叫做变量 x 的增量,记作 Δx ,即 2 1 Δx = − x x . 显然,增量 Δx 可以是正的,也可以是负的. 2 1 Δ= − y fx fx () () 叫做函数值的增量. 一般地,设函数 y f = ( ) x 在点 0 x 的某一个邻域内是有定义的. 当自变量 x 在这邻域内从 0 x 变到 0 x x + Δ 时,函数值 y 相应 地从 0 f ( ) x 变到 0 f ( ) x x + Δ ,因此,函数 y 的对应增量为 0 0 Δ = +Δ − y fx x fx ( ) ()

2.连续的定义(Definition of Continuity) 定义1设函数f(x)在U(x。)内有定义,如果当自变量的增量 △x趋向于零时,对应的函数的增量△y也趋向于零,即im△y=0 △x→0 或im[f(x。+△x)-f(x川=0,那末就称函数f(x)在点连续, 并称飞。为f(x)的连续,点. 说明:由△x=x-x,则△x→0就是x→x。·又因为 △y=f(x+△x)-f(x)=f(x)-f(x), 即f(x)=△y+f(x), 则△y→0,也就是f(x)→f(x),于是有以下等价定义: 2009年7月3日星期五 4 目录 上页 下页 返回
2009年7月3日星期五 4 目录 上页 下页 返回 定义 1 设函数 xf )( 在 )( 0 2. 连续的定义 (Definition of Continuity ) U x δ 内有定义,如果当自变量的增量 Δx趋向于零时 , 对应的函数的增量 Δy也趋向于零 , 即 lim 0 0 Δ = Δ → y x 或 lim 0 ()([ 0 )] 0 0 Δ+ − = →Δ f x x f x x ,那末就称函数 f x)( 在点 x 0连续 , 并称 x 0 为 f x)( 的连续点. 说明: 由 Δx = 0 x − x , 则 Δx → 0就是 0 x x → .又因为 0 0 0 Δ= − = − y f fx f ( ) ( ) () ( ) x + Δx x f x , 即 0 f y () ( ) x = Δ + f x , 则 Δy → 0, 也就是 0 fx fx () ( ) → , 于是有以下等价定义:

定义2设函数y=f(x)在x的某邻域内有定义,且 limf(x)=f(xo),则称函数f(x)在x连续, x→x0 采用£-6”语言,定义2可叙述为: 对£>0,ヨ6>0,当x-x<δ时,总有f(x)-f(x<e 成立,则称函数y=f(x)在点x连续. 注意定义1与定义2本质上是一致的,即函数f(x)在 点x,连续,必须同时满足下列三个条件: (1)函数y=f(x)在点x的某个邻域内有定义 (2)limf(x)存在; (3)lim f(x)=f(xo). x→xXg 2009年7月3日星期五 5 目录 上页 下页 返回
2009年7月3日星期五 5 目录 上页 下页 返回 y = f x)( 在 0 x 的某邻域内有定义 , 0 ,)()(lim0 f x f x xx = → .)( 在xxf 0 连续 采用 “ 则称函数 定义 2 设函数 且 ε − δ ”语言,定义 2 可叙述为: 对 ∀ ε > 0 ,∃ δ > 0 ,当 0 x x − < δ 时,总有 0 fx fx () ( ) − < ε 成立,则称函数 y fx = ( ) 在点 0 x 连续. 注意 定义 1 与定义 2 本质上是一致的,即函数 f ( ) x 在 点 0 x 连续,必须同时满足下列三个条件: ( 1 ) 函数 y = f ( ) x 在点 0 x 的某个邻域内有定义 ( 2 ) 0 lim ( ) x x f x → 存在; ( 3 ) 0 0 lim ( ) ( ) x x fx fx → = .

3.单侧连续(One-sided Continuity) 左连续(Left Continuity): 与单侧极限 f(xo)=lim f(x)=f(x) 相类似! x→x0 8>0,3δ>0,当x∈(x-6,) 时,有f(x)-f(x)0,36>0,当x∈(x0,x0+δ) 时,有f(x)-f(x)川<8. 定理 lim f(x)=f(xo)1 lim f(x)=lim f(x)=f(xo) X→X0 x-→x0 x→x0 2009年7月3日星期五 6 目录上页 下页 、返回
2009年7月3日星期五 6 目录 上页 下页 返回 3. 单侧连续(One-sided Continuity) 左连续 (Left Continuity) : = − )( 0xf 0 0 lim ( ) ( ) x x f x f x → − = ∀ ε > ,0 ∃ δ > ,0 当 ),( 0 0 ∈ − δ xxx 时, 有 0 f x() . − f x( ) ,0 ∃ δ > ,0 当 ),( ∈ xxx 00 + δ 时, 有 0 f x() . − f x( ) < ε 0 0 lim ( ) ( ) x x 定理 f x f x → = 0 0 0 lim ( ) lim ( ) ( ) xx xx fx f x f x → → + − = = 与单侧极限 相类似!

4.连续函数(Continuous Function) 若∫(x)在某区间上每一点都连续,则称它在该区间上 连续,或称它为该区间上的连续函数. 如果此区间包含端点,那么 (1)函数在左端,点连续是指在左端,点右连续, (2)函数在右端,点连续是指在右端,点左连续, 连续函数的图形是一条连续而不间断的曲线。 在闭区间[a,b]上的连续函数的集合记作C[a,b] 2009年7月3日星期五 目录 上页 下页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 4. 连续函数(Continuous Function) 若 f x)( 在某区间上每一点都连续 , 则称它在该区间上 连续 , 或称它为该区间上 的连续函数 . 如果此区间包含端点,那么 ( 1)函数在 左端点连续是指 在 左端点 右连续, ( 2)函数在 右端点连续是指 在 右端点 左连续 . 连续函数的图形是一条连续 而不间断的曲线. 在闭区间 ba ],[ 上的连续函数的集合记作 C ba .],[

例如,P(x)=a+4x+.+anx”(有理整函数) 在(-0,+0)上连续. 又如,有理分式函数R(x)= P(x) e(x) 在其定义域内连续。 只要Q(xo)≠0,都有limR(x)=R(xo) x-→x0 2009年7月3日星期五 8 目录 上页下页 、返回
2009年7月3日星期五 8 目录 上页 下页 返回 )()(lim,),( 0 0 0 x P x P x xx −∞∈∀ + ∞ = → n n )( 10 "+++= xaxaaxP 在 − ∞ + ∞),( 上连续 . ( 有理 整函数 ) 又如 , 有理分式函数 )( )( )( xQ P x xR = 在其定义域内连续 . 只要 ,0)(xQ 0 ≠ 都有 0 )()(lim0 R x R x xx = → 例如

例1证明函数y=Sinx在(-o0,+oo)内连续. 证:x∈(-00,+0) △y=sin(x+△x)-sinx=2sinA,'cos(x+2) |Ay川=2sin÷cos(x+=) ≤21=Ax △x→0 0 即 lim△y=0 △x>0 这说明y=sinx在(-oo,+o)内连续. 同样可证:函数y=c0Sx在(-0,+∞)内连续. 2009年7月3日星期五 9 目录 上页 下页 返回
2009年7月3日星期五 9 目录 上页 下页 返回 y = sin x 在 − ∞ + ∞),( 内连续 . 证: ∀ x −∞∈ + ∞),( y =Δ + Δ − sin)sin( xxx )cos(sin2 2 2 x x x Δ Δ = + 2 2 2 sin cos( ) x x y x Δ Δ Δ= ⋅ + 12 2 ⋅≤ Δ x = Δ x x →Δ 0 即 0lim0 Δ = →Δ y x 这说明 y = sin x 在 − ∞ + ∞),( 内连续 . 同样可证: 函数 y = cos x 在 −∞ + ∞),( 内连续 . 0 例1 证明函数

2x+1,x≥0 例2讨论函数y= 在x=0处的连续性. 3x-1,x<0 解由于limy=lim(3x-1)=0-1=-1 x-→0 limy=lim(2x+1)=0+1=1 x→0 x→0+ 即左右极限不相等,所以该函数在x=0点不连续。 但是,因为f(0)=1=f(0),所以函数y在x=0处 右连续. 2009年7月3日星期五 10 目录○ (上页下页 返回
2009年7月3日星期五 10 目录 上页 下页 返回 2 1, 0 3 1, < 0 x x y x x ⎧ + ≥ = ⎨ ⎩ − x = 0 0 0 lim lim(3 1) 0 1 1 x x y x → → − − = − = − =− 0 0 lim lim(2 1) 0 1 1 x x y x → → + + = + = += x = 0 f f (0) 1 (0 ) + = = y x = 0 例 2 讨论函数 在 处的连续性. 解 由于 即左右极限不相等,所以该函数在 点不连续. 但是,因为 ,所以函数 在 处 右连续.