
第二章 第一节导数概念 (The Concept of Derivative) 一、引例 二、导数的定义 三、导数的几何意义 四、函数的可导性与连续性的关系 五、小结与思考题 2009年7月3日星期五 2 目录 上页 下页 、返回
2009年7月3日星期五 2 目录 上页 下页 返回 第一节 导数概念 第二章 三、导数的几何意义 二、导数的定义 一、引 例 四、函数的可导性与连续性的关系 五、小结与思考题 (The Concept of Derivative )

一、引例(Introduction) O 1.变速直线运动的速度 设描述质,点运动位置的函数为 s=f(t) 则to到t的平均速度为 i-I()-S(to) 自由落体运动 t-to s=g12 而在t,时刻的瞬时速度为 (to) v=lim ∫()-f() 0 to t→o t-to 2009年7月3日星期五 3 目录 上页>下页 返回
2009年7月3日星期五 3 目录 上页 下页 返回 一、引 例 (Introduction ) 1. 变速直线运动的速度 设描述质点运动位置的函数为 s = f t)( 0 t 则 到 的平均速度为 0 t t v = )()( 0 f t − f t 0 t − t 而在 时刻的瞬时速度为 0 t 0 lim t t v → = 0 f () ( ) t ft − 0 t t − 1 2 2 s gt = s o )( 0tf tf )( t 自由落体运动
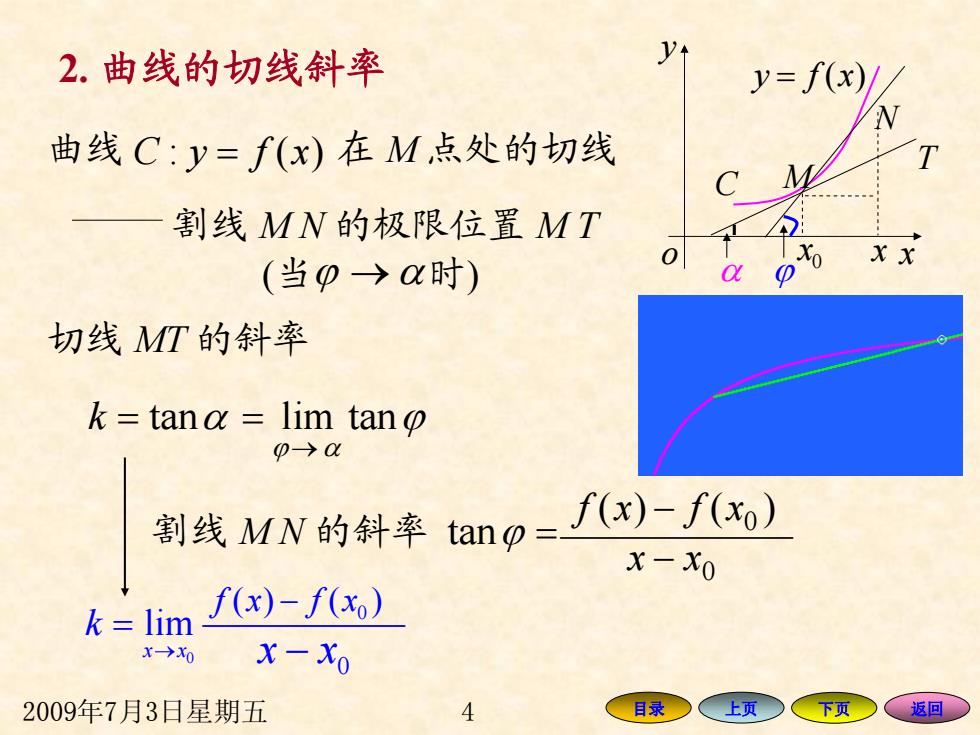
2.曲线的切线斜率 y=f(x)/ 曲线C:y=f(x)在M点处的切线 割线MN的极限位置MT (当0→时) xx 切线MT的斜率 k =tana lim tan 0→ 割线MW的斜率tan0=)-fo) x-x0 k=lim f(x)-f(x.) x→x0 x-Xo 2009年7月3日星期五 4 目录○ 上页 下页 、返回
2009年7月3日星期五 4 目录 上页 下页 返回 曲线 C y = f x)(: 割线 M N 的极限位置 M T 在 M 点处的切线 (当 时 ϕ → α ) 2. 曲线的切线斜率 x y o = xfy )( C α ϕ N T 0 x M x 割线 M N 的斜率 tan ϕ = )()( 0 f x − f x 0 − xx 切线 MT 的斜率 k = tan α ϕ αϕ tanlim→ = 0 lim x x k → = 0 f () ( ) x fx − 0 x x −

f(to) 瞬时速度v=lim f(t)-f() t→to t-to y=f(x 切线斜率k=lim f(x)-f(xo) X→X0 x-x0 M 两个问题的共性: X 所求量为函数增量与自变量增量之比的极限 类似问题还有: 加速度是速度增量与时间增量之比的极限 角速度是转角增量与时间增量之比的极限 线密度是质量增量与长度增量之比的极限 化率问题 电流强度是电量增量与时间增量之比的极限 2009年7月3日星期五 5 目录 上页 下页 返回
2009年7月3日星期五 5 目录 上页 下页 返回 s o 0 t )( 0tf tf )( 瞬时速度 t lim0tt v → = )()( 0 f t − f t 0 t − t 切线斜率 x y o = xfy )( C α ϕ N T 0 x M x lim0xx k → = )()( 0 f x − f x 0 − xx 两个问题的共性: 所求量为函数增量 与自变量增量之比的极限 . 类似问题还有: 加速度 是速度增量 与时间增量之比的极限 角速度 线密度 电流强度 是转角增量 与时间增量之比的极限 是质量增量 与长度增量之比的极限 是电量增量 与时间增量之比的极限 变化率问题

二、导数的定义(Definition of Derivatives) 1.函数在一点的导数与导函数 定义1设函数y=f(x)在点x的某邻域内有定义 若 y limf)-fx,)=limA △y=f(x)-f(x) X→x0 x-xo △x0△X △X=x-Xo 存在,则称函数f(x)在,点x处可导,并称此极限为 y=f(x)在点xo的导数.记作: dy yx=0;∫'(xo);dxx=x0 df(x) dxx=xo 即yx=0=f'(xo)=limA9 Ax→0△X lim f(o+Ax)-f(xo) lim f(xo+h)-f(xo) △x-→0 △x -→0 h 2009年7月3日星期五 6 目录 、上页 下页 返回
2009年7月3日星期五 6 目录 上页 下页 返回 二、导数的定义 (Definition of Derivatives ) 1. 函数在一点的导数与导函数. 定义 1 设函数 = xfy )( 在点 0 x 0 limx → x 0 0 f () ( ) x fx x x − − 0 limx y Δ → x Δ = Δ )()( 0 Δ = − xfxfy 0 Δ = − xxx 存在, xf )( 并称此极限为 = xfy )( 记作: ; 0xx y = ′ ;)( 0 f ′ x ; d d 0 x xx y = d 0 )(d x xx f x = 则称函数 若 的某邻域内有定义 , 在点 0 x 处可导, 在点 0 x 的导数. 0xx y = ′ )( 0 = f ′ x 0 limx y Δ → x Δ = Δ x f x x f x x Δ + Δ − = →Δ )()( lim 0 0 0 h f x h f x h )()( lim 0 0 0 + − = → 即

lim f(x)-f(%o)=lim Ay △y=f(x)-f(xo) x→X0 x-X0 △x→0△X △x=X-Xo 若上述极限不存在,就说函数在点x不可导 若mA业=o,也称f(x)在x,的导数为无穷大 △x0△X 若函数在开区间I内每,点都可导,就称函数在1内可导 此时导数值构成的新函数称为导函数 记作:y;f(x); dy.df(x) dx dx 注意:"(x)=∫"(x)x=0≠ df(xo) dx 2009年7月3日星期五 7 目录 上页 下页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 若上述极限不存在 , 在点 不可导. 0 x 若 0 lim , x y Δ → x Δ = ∞ Δ 也称 f x)( 在 0 x 若函数在开区间 I 内每点都可导, 此时导数值构成的新函数称为导函数. 记作: y′ ; ′ xf ;)( ; d d x y . d )(d x f x 注意: )( 0 ′ xf 0 )( xx xf = = ′ x f x d d )( 0 ≠ 就说函数 就称函数 在 I 内可导. 的导数为无穷大 . 0 lim →xx 0 0 )()( xx xfxf − − x y x Δ Δ = →Δ 0 lim )()( 0 Δ = − xfxfy 0 Δ = − xxx

由此可见, 运动质,点的位置函数 s=f(t) f(t) 在时刻的瞬时速度 o to v=lim f)-fi)=f'u,) t→to t-to 曲线C:y=f(x)在M点处的切线斜率 k=lim f(x)-f(x) y=f(x) x→x0 x-Xo CM∠ =f'(x) 2009年7月3日星期五 8 目录 上页 下页 、返回
2009年7月3日星期五 8 目录 上页 下页 返回 由此可见, s = f t( ) s o 0 t )( 0tf tf )( t 在 时刻的瞬时速度 0 t 运动质点的位置函数 lim0tt v → = )()( 0 − tftf 0 − tt 曲线 C : ( y f = x ) 在 M 点处的切线斜率 x y o = xfy )( C α N T 0 x M x lim 0xx k → = )()( 0 − xfxf 0 − xx 0 = f ′( ) t 0 = f ′( ) x

2.求导数举例. 例1求函数f(x)=C(C为常数)的导数 解:y=lim f+A)-fw=1imC-C =0 △x-→0 △x △x-→0△x 即 (C)y=0 例2求函数f(x)=x”(n∈N)在x=a处的导数 解:f'a)=limf()-fa=limx”-a x→a x-a x→ax-a lim(x"+axa-2+a2x3+.+a"-l) x→a =nan-l 2009年7月3日星期五 9 目录 上页 下页 返回
2009年7月3日星期五 9 目录 上页 下页 返回 f )( = Cx y′ ( C 为常数) 的导数. 解 : x C C x Δ − = →Δ 0 lim = 0 即 C ′ = 0)( 例 2 求函数 )N()( + nxxf ∈= n 在 = ax 处的导数. 解 : ax f x f a − − )()( →ax f ′ a)( = lim ax ax nn ax − − = → lim (lim→ax = n − 1 x − 2 + n xa −32 + n a x + " ) − 1 + n a − 1 = n an x f xx f x Δ + Δ − )()( 0 lim →Δ = x 例 1 求函数 2. 求导数举例

说明: 对一般幂函数y=x“(山为常数) (x“y=hx (以后将证明) 例如,=gy-2 ()=xy=-x-1= 3 7 4 2009年7月3日星期五 10 目录 上页 下页 返回
2009年7月3日星期五 10 目录 上页 下页 返回 对一般幂函数 y x μ = ( μ 为常数) 1 ( ) x x μ μ μ − ′ = 例如, x )( ′ )( 2 1 = x ′ 2 1 2 1 − = x 2 x 1 = ( ) ′ x 1 )( 1 = ′ − x −− 11 −= x 2 1 x − = ) 1 ( ′ xx )( 4 3 = ′ − x 4 7 4 − 3 − = x (以后将证明) 说明:

例3设函数f(x)=sinx,求(sinx)'及(sinx)g 解:((sinx)=lim in(x+h)-sinx h-→0 h h h、 limcos(x+). 2 =coSx. h-→0 2 h 2 即(sinx)'=cosx. .in cosx 2 2 类似可证得:(cosx)/=-sinx 2009年7月3日星期五 11 目录○ 、上页) 下页 、返回
2009年7月3日星期五 11 目录 上页 下页 返回 类似可证得: (cos ) sin x ′ = − x 例 3 解: 0 sin( ) sin (sin ) limh x h x x → h + − ′ = 0 sin 2 limcos( ) 2 2 h h h x → h = +⋅ = cos . x (sin ) cos . x ′ = x 4 4 (sin ) cos x x x x π π = = ∴ = ′ 2 . 2 = 设函数 f ( ) sin , x x = 求(sin ) x ′及 4 (sin ) x ′ π 即