
第四章 不定积 Indefinite Integrals) 微分法:F'(x)=(?) 互逆运算 积分法:(?)'=f(x) 2009年7月3日星期五 2 目录 上页 下页 、返回
2009年7月3日星期五 2 目录 上页 下页 返回 微分法 : ′ xF = )?()( 积分法 : ′ = f x)()?( 互逆运算 第四章 不定积分 (Indefinite Integrals )

主要为容 第一节不定积分的概念与性质 第二节 换元积分法 第三节分部积分法 第四节几种特殊类型函数的积分 第五节积分表的使用 2009年7月3日星期五 3 目录 上页 下页 返回
2009年7月3日星期五 3 目录 上页 下页 返回 主要内容 第一节 不定积分的概念与性质 第二节 换元积分法 第三节 分部积分法 第四节 几种特殊类型函数的积分 第五节 积分表的使用

第四章 第一节不定积分的橇念与性质 (Conceptions and properties of Indefinite Integrals) 一、原函数与不定积分的概念 二、基本积分表 三、不定积分的性质 四、小结与思考题 2009年7月3日星期五 4 目录 上页今 下页 、返回
2009年7月3日星期五 4 目录 上页 下页 返回 第一节 不定积分的概念与性质 第四章 一、原函数与不定积分的概念 二、基本积分表 (Conceptions and properties of Indefinite Integrals ) 三、不定积分的性质 四、小结与思考题

一、原函数与不定积分的概念 (Primitive Function and the Indefinite Integral) 定义1若在区间I上定义的两个函数F(x)及f(x) 满足F'(x)=f(x)或dF(x)=f(x)dx,则称F(x)为f(x) 在区间1上的一个原函数. 例如,-sint的原函数有cost,cost+3,. 问题: 1.在什么条件下,一个函数的原函数存在? 2.若原函数存在,它如何表示? 2009年7月3日星期五 6 目录○ 上页 下页 、返回
2009年7月3日星期五 5 目录 上页 下页 返回 一、原函数与不定积分的概念 (Primitive Function and the Indefinite Integral) 定义 1 若在区间 I 上定义的两个函数 F (x) 及 f (x ) 满足 F′ x = f x)()( 或 = xxfxF ,d)()(d 在区间 I 上的一个原函数 . 则称 F (x) 为f (x) 例如, −sin t 的原函数有 t,cos t + ,3cos " 问 题: 1. 在什么条件下, 一个函数的原函数存在 ? 2. 若原函数存在, 它如何表示 ?

定理1(原函数存在定理)若函数f(x)在区间I上连续, 则f(x)在I上存在原函数. (下章证明) 初等函数在定义区间上连续 初等函数在定义区间上有原函数 2009年7月3日星期五 6 目录 上页下页 、返回
2009年7月3日星期五 6 目录 上页 下页 返回 定理 1(原函数存在定理)若函数 )( 在区间Ixf 上连续, )( Ixf 上在则 存在原函数 . (下章证明 ) 初等函数在定义区间上连续 初等函数在定义区间上有原函数

定理2若F(x)是f(x)的一个原函数,则f(x)的所有 原函数都在函数族F(x)+C(C为任意常数)内. 证:1)(F(x)+C)}=F'(x)=f(x) ∴.F(x)+C是f(x)的原函数 2)设D(x)是f(x)的任一原函数,即 Φ'(x)=f(x) 又知 F'(x)=f(x) .[Φ(x)-F(x)]'=Φ'(x)-F'(x)=f(x)-f(x)=0 故 ①(x)=F(x)+Co(C0为某个常数) 即①(x)=F(x)+C属于函数族F(x)+C. 2009年7月3日星期五 目录 上页 下页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 是若 xfxF )()( 的一个原函数, 则 xf )( 的所有 原函数都在函数族 )( + CxF ( C 为任意常数 ) 内 . 证 : 1) ∴ + 是 xfCxF )()( 的原函数 ∵ + CxF ))(( ′= ′ xF )( = f x)( Φ 是设 xfx )()()2 的任一原函数, Φ′ x = f x)()( 又知 F′ x = f x)()( ∴ Φ − xFx ])()([ ′= Φ′ − ′ xFx )()( = f x − f x = 0)()( 故 0 Φ = )()( + CxFx ( ) C 0 为某个常数 即 0 Φ x = F x)()( + C 属于函数族 Fx C () . + 即 定理 2

定义2f(x)在区间I上的原函数全体称为f(x)在1 上的不定积分,记作∫f(x)dx,其中 ∫一积分号;f)一被积函数; x一积分变量;f(x)dx一被积表达式. 若F'(x)=f(x),则 f(x)dx=F(x)+C(C为任意常数) 例如,「edx=e+C C称为积分常数 ∫x2dr=x3+C 不可丢! sin xdx=-cosx+C 2009年7月3日星期五 8 目录 上页 下页 、返回
2009年7月3日星期五 8 目录 上页 下页 返回 f x)( 在区间 I 上的原函数全体称为 )( 在Ixf 上的不定积分, xxf ,d)( ∫ 其中 ∫ — 积分号 ; f x)( — 被积函数 ; x — 积分变量 ; f d)( xx — 被积表达式 . 若 F′ x = f x ,)()( 则 += CxFxxf ∫ )(d)( ( C 为任意常数 ) C 称为积分常数 不可丢 ! 例如 , = ∫ xex d Cex + = ∫ dxx2 + Cx3 3 1 = ∫ dsin xx − cos x + C 记作 定义 2
不定积分的几何意义: f(x)的原函数的图形称为f(x)的积分曲线 ∫f(x)dr的图形一f(x)的所有积分曲线组成 的平行曲线族, Xo 2009年7月3日星期五 9 目录 上页 下页 返回
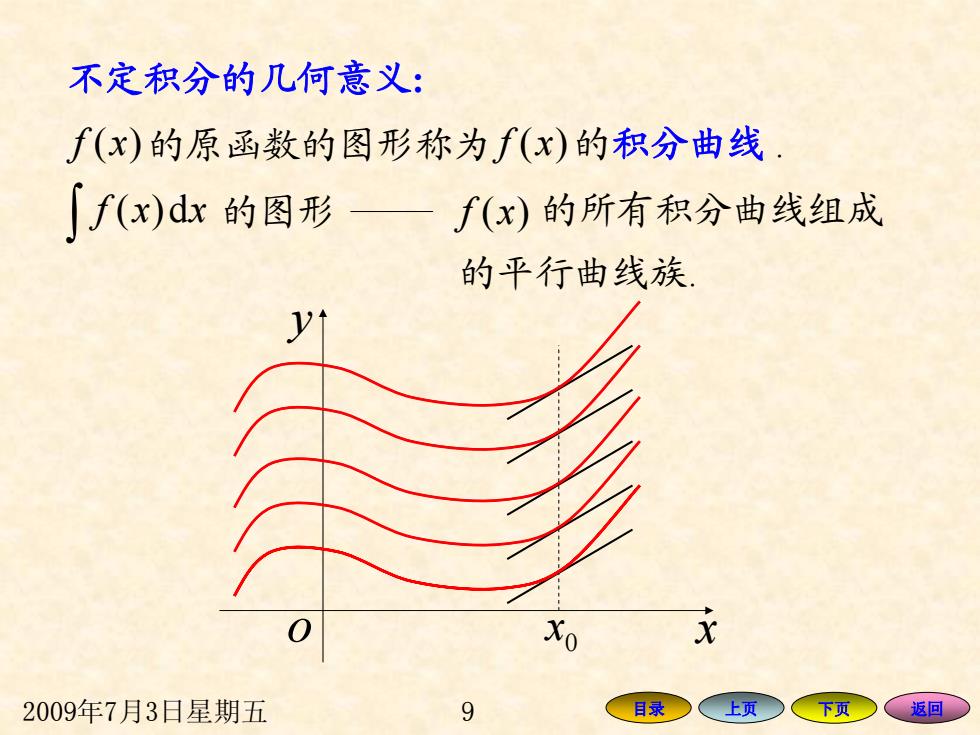
2009年7月3日星期五 9 目录 上页 下页 返回 f x)( 的原函数的图形称为 f x)( d)( xxf ∫ 的图形 f x)( 的所有积分曲线组成 的平行曲线族. y o x 0 x 的积分曲线 . 不定积分的几何意义 :

从不定积分定义可知: ax]-f)或dj/et]=fe)d ∫F'(x)dx=F(x)+C或∫dF(x)=F(x)+C (2) 二、基本积分表 利用逆向思维 () ∫kdr=kx+C (k为常数) (2)∫x“d=Hx1+C (u≠-1) (3) x<0时 (Inxy=[In(-x)=I 2009年7月3日星期五 10 目录 上页 下页 返回
2009年7月3日星期五 10 目录 上页 下页 返回 [ d x d )1( ∫ d)( xxf ] = f x)( 二、 基本积分表 从不定积分定义可知 : d [ ∫ 或 d)( xxf ] = f x d)( x += Cx ∫ F′ x)( d)2( F x)( 或 += C ∫ d F x)( F x)( 利用逆向思维 = ∫ d)1( xk k x + C ( k 为常数 ) = ∫ d)2( xxμ + Cx + + 1 1 1 μ μ = ∫ x d x )3( ln + Cx x < 0 时 μ ≠ − )1( ′ = −xx ])ln([)ln( ′ x 1 =

(4) dx arctanx+C-arccotx+C J1+x (5) dx arcsinx+C-arccosx+C √1-x2 (6) [cosxdx=sinx+C (7)sinxdx =-cosx+C (oee dstnxc ,-小w=-a+d 2009年7月3日星期五 11 目录 上页 下页 、返回
2009年7月3日星期五 11 目录 上页 下页 返回 = + ∫ 2 1 d )4( x x arctan + Cx = ∫ dcos)6( xx sin + Cx = ∫ x x 2 cos d )8( = ∫ dsec xx 2 tan + Cx 或 − cotarc + Cx = − ∫ 2 1 d )5( x x arcsin + Cx 或 − cosarc + Cx = ∫ dsin)7( xx − cos + Cx = ∫ x x 2 sin d )9( = ∫ dcsc xx 2 − cot + Cx