
第六章 第五节平面及其方程 The Planes and Its Equations) 一、平面的点法式方程 二、平面的一般方程 三、两平面的夹角 四、小结与思考练习 2009年7月3日星期五 目录 上页 下页 返回
2009年7月3日星期五 1 目录 上页 下页 返回 第五节 平面及其方程 第六章 (The Planes and Its Equations) 四、小结与思考练习 一、平面的点法式方程 二、平面的一般方程 三、两平面的夹角

一、平面的点法式方程 (The Point-Normal Form Equations of a Plane) 设一平面通过已知点M(x0,y0,2o)且垂直于非零向 量=(A,B,C),求该平面Π的方程. nt 任取点M(x,y,z)∈I,则有 MoM⊥ 故 MoM.n=0 /X y M0M=(x-x0,y-y0,2-20) A(x-xo)+B(y-yo)+C(z-20)=0 ① 称①式为平面Π的点法式方程,称为平面Ⅱ的法向量. 2009年7月3日星期五 2 目录 上页 下页 返回
2009年7月3日星期五 2 目录 上页 下页 返回 Π z y x o M 0 n ① 一、平面的点法式方程 ),( 0000 zyxM 且垂直于非零向 0)()()( 0 0 0 设一平面通过已知点 − xxA + B y − y + C z − z = M 称①式为平面 Π 的点法式方程, 求该平面 Π的方程. 任取点 zyxM ∈ Π,),( ),( 000 − xx y − y z − z 法向量. 量 = An B C ,),( M M ⊥ n 0 0 M 0 M ⋅n = M 0 M = 则有 故 称 n 为平面 Π 的 (The Point-Normal Form Equations of a Plane)

例1求过三点M1(2,-1,4),M2(-1,3,-2),M3(0,2,3) 的平面Π的方程.(自学课本例2) 解:取该平面Π的法向量为 nt i=M1M2×M1M3 M M3 i方 -34-6 M2 -23-1 =(14,9,-1) 又M1∈Π,利用,点法式得平面Π的方程 14(x-2)+9(y+1)-(z-4)=0 即 14x+9y-z-15=0 2009年7月3日星期五 3 目录○ 上页 下页 、返回
2009年7月3日星期五 3 目录 上页 下页 返回 i j k = , 又 M 1 ∈ Π = − )1,9,14( x − + y + − z − = 0)4()1(9)2(14 即 x + y − z − = 015914 M 1 M 2 M 3 解 : 取该平面 Π 的法向量为 ),2,3,1(),4,1,2( M 1 − M 2 − − )3,2,0( M 3 的平面 Π 的方程. (自学课本 例 2 ) 利用点法式得平面 Π 的方程 ∏ − 3 4 − 6 − 2 3 1− n n = M M × M M3121 例1 求过三点

说明:此平面的三点式方程也可写成 x-2y+1z-4 -34-6=0 -23-1 一般情况:过三点Mk(xk,yk,3k)(k=1,2,3) 的平面方程为 x-x1 y-y z-21 x2-1y2-y1 22-21 =0 X3-X1 y3-y1 23-21 2009年7月3日星期五 4 目录○ 上页 下页 返回
2009年7月3日星期五 4 目录 上页 下页 返回 此平面的三点式方程也可写成 0 132 643 = − − − − x − y + z − 412 0 131313 121212 1 1 1 = −−− −−− − − − zzyyxx zzyyxx yyxx z z 一般情况 : 过三点 M x y z k = )3,2,1(),( k k k k 的平面方程为 说明 :

特别,当平面与三坐标轴的交点分别为 P(a,0,0),Q(0,b,0),R(0,0,c) 时,平面方程为 x+y+2=1(a,b,c≠0) a b c 此式称为平面的截距式方程. 分析:利用三点式 x-a y Z -a b0=0 -a 0 按第一行展开得(x-a)bc-y(-a)c+zab=0 即 bcx acy +abz abc 2009年7月3日星期五 5 目录 上页 下页 、返回
2009年7月3日星期五 5 目录 上页 下页 返回 此式称为平面的截距式方程. P bQa R c),0,0(,)0,0(,)0,0,( =++ 1 c z b y a x )0,( 时, cba ≠ − )( bcax − y − )( ca + z ba = 0 bcx + y +aac z = abcb 平面方程为 P o z y x R Q 分析:利用三点式 按第一行展开得 即 = 0 − ax y z − a b 0 − a 0 c 特别,当平面与三坐标轴的交点分别为

二、平面的一般方程(General Equation of a Plane) 设有三元一次方程 Ax+By+Cz+D=0(42+B2+C20) 任取一组满足上述方程的数x0,y0,20,则 4x0+Byo+Czo+D=0 以上两式相减,得平面的点法式方程 A(x-xo)+B(y-y0)+C(2-20)=0 显然方程②与此,点法式方程等价,因此方程②的图形是 法向量为n=(A,B,C)的平面,此方程称为平面的一般 方程. 2009年7月3日星期五 6 目录 上页 下页 、返回
2009年7月3日星期五 6 目录 上页 下页 返回 二、平面的一般方程 设有三元一次方程 0 以上两式相减 , 得平面的点法式方程 此方程称为平面的一般 xA + B + Cy z + D = 任取一组满足上述方程的数 , 000 yx z 则 0)()()( − xxA 0 + B y − y 0 + C z − z 0 = 0 xA + B y + C z000 + D = 显然方程②与此点法式方程等价, ( )0 222 CBA ≠++ ② 法向量为 = An B C),( 的平面, 因此方程②的图形是 方程. (General Equation of a Plane )

Ax+By+Cz+D=0(42+B2+C20) 特殊情形 ·当D=0时,Ax+By+Cz=0表示通过原点的平面; ·当A=0时,By+Cz+D=0的法向量 n=(0,B,C)⊥i,平面平行于x轴; ·Ax+Cz+D=0表示平行于y轴的平面; ·Ax+By+D=0表示平行于z轴的平面; ·Cz+D=0表示平行于xoy面的平面; ·Ax+D=0表示平行于y0z面的平面; ·By+D=0表示平行于0x面的平面. 2009年7月3日星期五 7 目录 上页 下页 、返回
2009年7月3日星期五 7 目录 上页 下页 返回 + + + DCzByAx = 0 特殊情形 ( )0 222 CBA ≠++ • 当 D = 0 时, A x + B y + C z = 0 表示通过原点的平面; • 当 A = 0 时, B y + C z + D = 0 的法向量 平面平行于 x 轴; • A x+C z+D = 0 表示 • A x+B y+D = 0 表示 • C z + D = 0 表示 • A x + D =0 表示 平行于 xoy 面 的平面; 平行于 yoz 面 的平面; • B y + D =0 表示平行于 zox 面 的平面. 平行于 y 轴的平面; 平行于 z 轴的平面; n = B C ⊥ i,),0(

例2求通过x轴和,点(4,-3,-1)的平面方程 解:因平面通过x轴,故A=D=0 设所求平面方程为 By+Cz=0 代入已知点(4,-3,-1)得C=-3B 化简,得所求平面方程 y-3z=0 (自学课本例3) 例3用平面的一般式方程导出平面的截距式方程. (自学课本例4) 2009年7月3日星期五 8 目录 上页 下页 、返回
2009年7月3日星期五 8 目录 上页 下页 返回 解 : 因平面通过 x 轴 , 故 A = D = 0 设所求平面方程为 By Cz + = 0 代入已知点 − − )1,3,4( 得 C = − 3 B 化简,得所求平面方程 y − z = 03 例2 求通过 x 轴和点( 4, – 3, – 1) 的平面方程. (自学 课本 例 3 ) 例 3 用平面的一般式方程导出平面的截距式方程. (自学课本 例 4 )
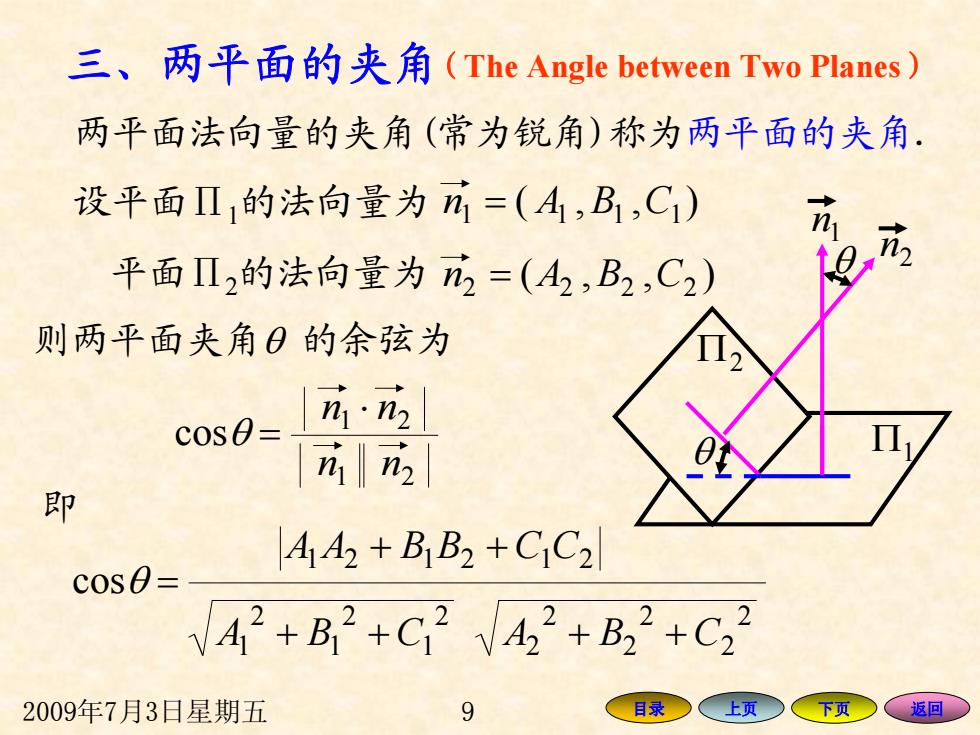
三、两平面的夹角(The Angle between Two Planes) 两平面法向量的夹角(常为锐角)称为两平面的夹角. 设平面Π1的法向量为n1=(A1,B1,C1) 平面Ⅱ2的法向量为2=(A2,B2,C2) 则两平面夹角0的余弦为 cos0= n应 in2 即 A42+B B2+C C2 c0S0= V42+B2+C7V42+B22+C22 2009年7月3日星期五 9 目录 上页 下页 返回
2009年7月3日星期五 9 目录 上页 下页 返回 三、两平面的夹角 设平面 ∏ 1的法向量为 平面 ∏ 2的法向量为 则两平面夹角 θ 的余弦为 cos θ = 即 + + CCBBAA 212121 2 2 2 2 2 2 ++ CBA 2 1 2 1 2 1 ++ CBA 两平面法向量的夹角(常为锐角)称为两平面的夹角. Π 1 Π 2 θ 2 n 1 n θ ),( = An B C1111 ),( = An B C2222 21 21 cos nn ⋅ nn θ = (The Angle between Two Planes )
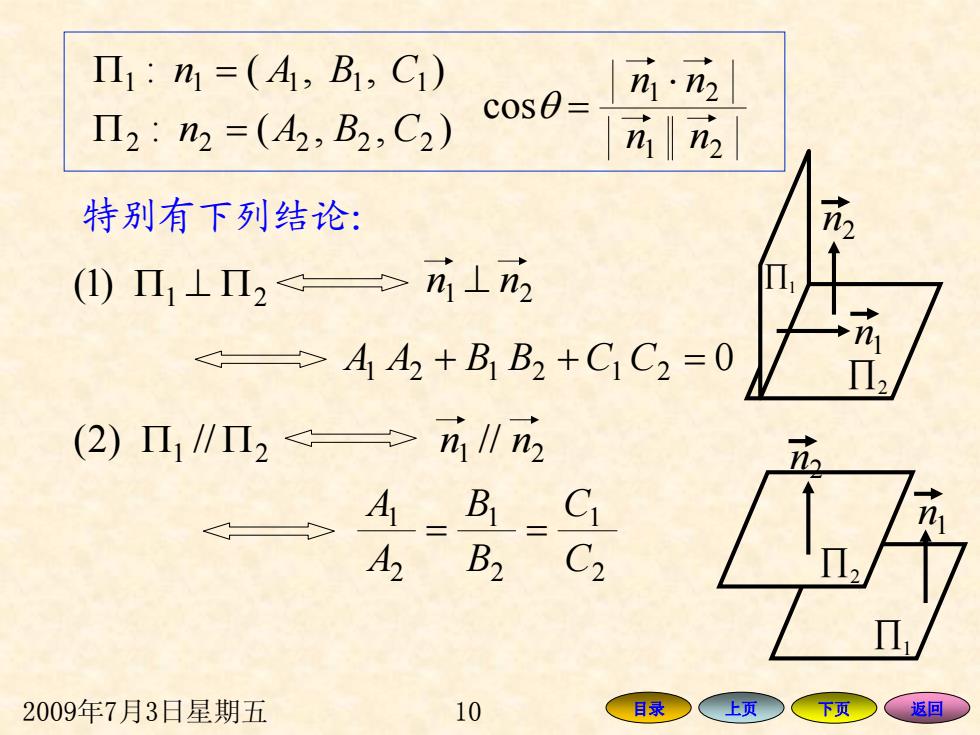
Π1:h1=(4,B,C1) h·n2 Π2:n2=(A2,B2,C2) c0s0= 2 特别有下列结论: 2 ()Π11Π2→⊥2 >A1A2+BB2+C1C2=0 (2)Π1∥Π2>i/∥n2 4B=C1 A2 B2 C2 2009年7月3日星期五 10 目录○ 上页 下页」 、返回
2009年7月3日星期五 10 目录 上页 下页 返回 ∏ 2 21 )1( Π Π⊥ 0 AA + B B + C C212121 = 21 Π //)2( Π 2 1 2 1 2 1 C C B B A A == ),(: ),(: 22222 11111 CBAn An B C =Π Π = ∏1 ∏1 ∏ 2 21 21 cos nn ⋅ nn θ = 21 ⊥ nn 21 // nn 2 n 1 n 2 n 1 n 特别有下列结论: