
第九章 第四节对面积的曲面积 Surface Integral for Area) 一、对面积的曲面积分的概念与性质 二、对面积的曲面积分的计算 三、小结与思考练习 2009年7月27日星期一 目录 上页 下页 、返回
2009年7月27日星期一 1 目录 上页 下页 返回 第四节 对面积的曲面积分 第九章 (Surface Integral for Area) 一、对面积的曲面积分的概念与性质 二、对面积的曲面积分的计算 三、小结与思考练习

一、对面积的曲面积分的概念与性质 1.曲面形构件质量的计算 如果把对孤长的曲线积分原型,即曲线形构件质量的 计算改成曲面形构件质量的计算,相应的线密度p(x,y) 改成面密度p(x,y,z),小段曲线的孤长△s改成小块曲面 的面积△S,第i小段曲线孤上所取的点(5,7,)改成第i小块 曲面上所取的点(5,7,5:),那么在面密度p(x,y,z)连续的条 件下,所求的曲面形构件的质量为 M=lim∑p(5,7,5i)AS, >0 其中入表示个小块曲面直径(即曲面中最长的弦)的最大值 2009年7月27日星期一 2 目录 上页 下页 、返回
2009年7月27日星期一 2 目录 上页 下页 返回 一、对面积的曲面积分的概念与性质 1. 曲面形构件质量的计算 如果把对弧长的曲线积分原型,即曲线形构件质量 的 计算改成曲面形构件质量的计算,相应的线密度 ρ(, ) x y 改成面密度 ρ(, ,) x y z ,小段曲线的弧长 Δ i s 改成小块曲 面 的面积 Δ Si ,第 i 小段曲线弧上所取的点(, ) i i ξ η 改成 第 i 小块 曲面上所取的点(, , ) iii ξ η ζ ,那么在面密度 ρ(, ,) x y z 连续的条 件下,所求的曲面形构件的质量为 0 1 lim ( , , ) n iii i i M S → = = ∑ Δ λ ρξ η ζ 其中 λ 表示 n 个小块曲面直径(即曲面中最长的弦)的最大值

2.对面积的曲面积分的概念 定义设∑为一光滑曲面(即曲面上处处有切平面, 并且当切,点在曲面上连续移动时,切平面也连续转动), 函数f(x,y,)在∑上有界.对∑作任意分割,将其分成n 小块△S(△S同时也表示第i块小曲面的面积,i=1,2,3, n),设(5,5)是△S,上任意取定的一点,作和 ∑f(5,5)△S,如果当各小块曲面的直径的最大值 无→0时,这和的极限m∑f(,5AS总存在,那么 称此极限值为f(x,y,z)在曲面∑上对面积的曲面积分 (或第一类曲面积分),记为∬f(x,八,)dS,即 2009年7月27日星期一 3 目录 上页 下页 返回
2009年7月27日星期一 3 目录 上页 下页 返回 2. 对面积的曲面积分的概念 定义 设 Σ 为一光滑曲面 (即曲面上处处有切平面, 并且当切点在曲面上连续移动时,切平面也连续转动 ), 函数 f xyz (, ,) 在 Σ 上有界. 对 Σ 作任意分割,将其分成 n 小块 i Δ S ( i Δ S 同时也表示第 i 块小曲面的面积,i =1,2,3, ⋅⋅⋅,n ), 设(, , ) iii ξ η ζ 是 i Δ S 上任意取定的一点, 作和 1 (, , ) n iii i i f S = ∑ ξηζ Δ , 如果当各小块曲面的直径的最大值, λ → 0 时, 这和的极限 0 1 lim ( , , ) n iii i i f S → = ∑ Δ λ ξηζ 总存在,那么 称此极限值为 f (, ,) xyz 在曲面 Σ 上对面积的曲面积分 (或第一类曲面积分 ), 记为 f ( , , )d xyz S Σ ∫∫ ,即

f.ds=m∑f5n,5)As, i≥1 其中f(x,y,)叫做被积函数,∑叫做积分曲面 如果Σ是闭曲面,那么该曲面积分就记为种f(x,y,2)dS 注意:从本节下一段的定理1将看到,当被积函数在 光滑曲面∑上连续时,对面积的曲面积分总是存在 的.如果未作特别说明,以后我们总假定被积函数在 上连续.前面讲到的曲面形构件的质量可表示为 M=∬px,y,z)dS 3.对面积的曲面积分的性质 具有对孤长的曲线积分相类似的性质,不再赘述! 2009年7月27日星期一 目录 上页 下页 返回
2009年7月27日星期一 4 目录 上页 下页 返回 f ( , , )d xyz S Σ ∫∫ = 0 1 lim ( , , ) n iii i i f S → = ∑ ⋅ Δ λ ξηζ , 其中 f (, ,) xyz 叫做被积函数,Σ 叫做积分曲面. 如果 Σ 是 闭曲面,那么该曲面积分就记为 f ( , , )d xyz S Σ w∫∫ . 注意:从本节下一段的定理 1将看到,当被积函数在 光滑曲面 Σ 上连续时, 对 面 积 的 曲面积分总是存在 的.如果未作特别说明,以后我们总假定被积函数在 Σ 上连续.前面讲到的曲面形构件的质量可表示为 M ( , , )d xyz S Σ = ∫∫ ρ . 3. 对面积的曲面积分的性质 具有对弧长的曲线积分相类似的性质,不再赘述!

二、对面积的曲面积分的计算 定理1设∑是光滑曲面,其方程为 z=z(x,y),(x,y)∈Dw, 其中D为∑在xOy面上的投影区域,函数z(x,y)在Dm 上具有连续的偏导数.又设被积函数f(x,y,)为定义在∑上 的连续函数,则曲面积分∬f(x,少,z)S存在,并且 ∬f,y,zas=∬f[x,y2(x,yV+z,(x,y)+,2(x,ydd (证明从略.) 2009年7月27日星期一 5 目录 上页 下页 返回
2009年7月27日星期一 5 目录 上页 下页 返回 二、对面积的曲面积分的计算 定理 1 设 Σ 是光滑曲面 ,其方程为 z = zxy (, ) ,(, ) xy xy D ∈ , 其中 D xy 为 Σ 在 xOy 面上的投影区域,函数 z(, ) x y 在 Dxy 上具有连续的偏导数. 又设被积函数 f (, ,) xyz 为定义在 Σ 上 的连续函数, 则曲面积分 f ( , , )d xyz S Σ ∫∫ 存在 ,并且 2 2 (, ,) [, , d 1 ( , ) ] ( , ) ( , ) d d xy x y D f xy f z z S z x y x y x y z x y x y Σ = + + ∫∫ ∫∫ (证明从略. )

若曲面∑:y=y(x,) 则∬fx,y)S =∬/x,yx,2,zV+y2+yd, 若曲面∑:x=x(y,) 则∬fx,y,z)d =∬/儿xy,y,2]V+x2+xd证 2009年7月27日星期一 6 目录 上页 下页 返回
2009年7月27日星期一 6 目录 上页 下页 返回 2 2 [, ,] (,) 1 ; xz x D z = fx z y x z + + y′ ′ y ddx z ∫∫ fx z (, ,) y dS Σ ∫∫ 则 2 2 [ ,] (,) 1 . yz y D z = f yz x y z + + x′ ′ xd z yd ∫∫ f yz (, ,) x dS Σ ∫∫ 若曲面 Σ : x = xyz (,) 则 若曲面 Σ : y yxz = ( )
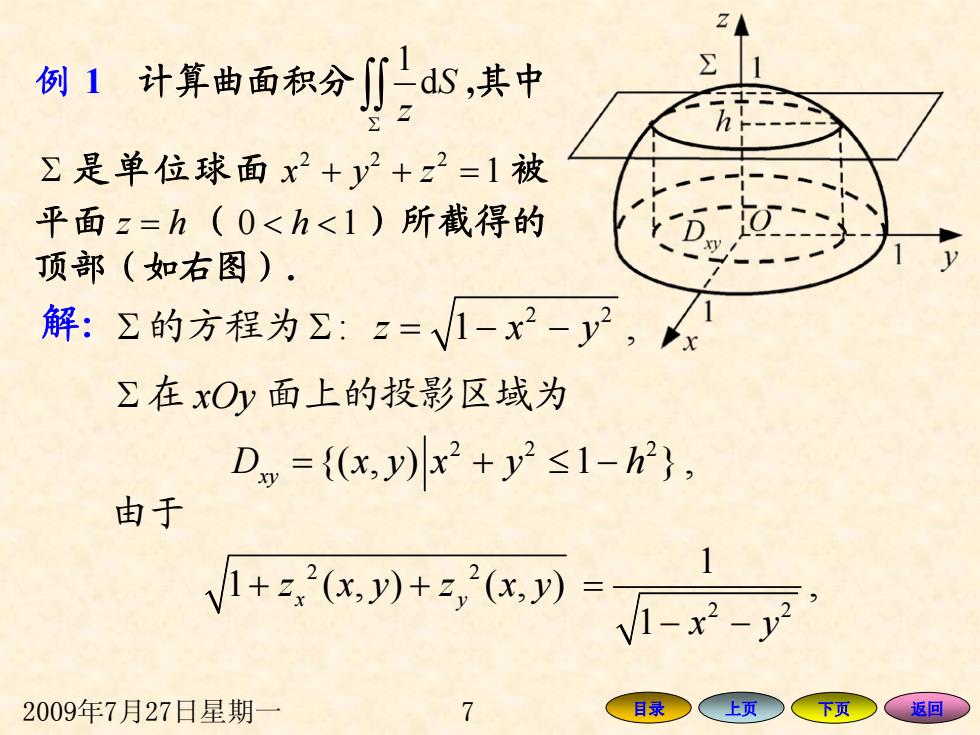
24 例1计算曲面积分dS,其中 Σ1 ∑是单位球面x2+y2+z2=1被 平面z=h(0<h<1)所截得的 顶部(如右图). 解:Σ的方程为公:z=V1-x2-y2, ∑在xOy面上的投影区域为 D,={(x,y)2+y≤1-h}, 由于 +x,+x功-x- 2009年7月27日星期一 7 目录○ 上页 下页 、返回
2009年7月27日星期一 7 目录 上页 下页 返回 例 1 计算曲面积分 1 d S z Σ ∫∫ ,其中 Σ 是单位球面 2 22 xyz + + = 1 被 平面 z = h ( 0 1 < h < ) 所截得 的 顶部(如右图). 解: Σ 的方程为 2 2 Σ =−− : 1 z x y , Σ 在 xOy 面上的投影区域为 22 2 {( , ) 1 } D xy x y h xy = + ≤− , 由于 2 2 1 (, ) (, ) x y + + z xy z xy 2 2 1 1 x y = − −
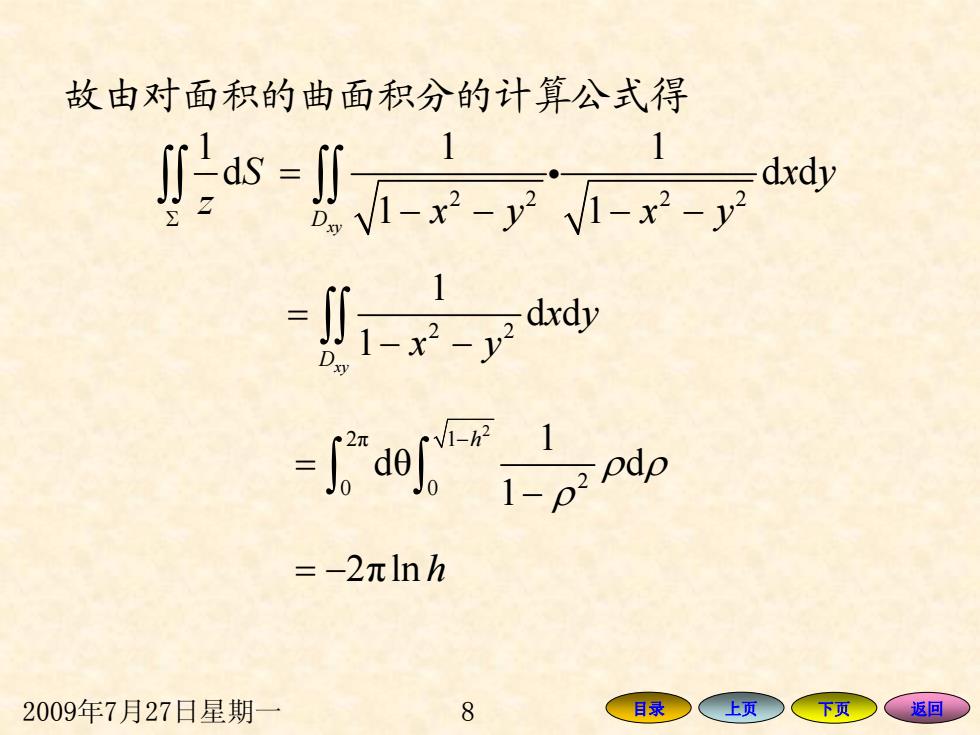
故由对面积的曲面积分的计算公式得 1-dy dxdy =川dd do =-2πlnh 2009年7月27日星期一 8 目录 上页> 下页 返回
2009年7月27日星期一 8 目录 上页 下页 返回 故由对面积的曲面积分的计算公式得 1 d S z Σ ∫∫ 22 22 d 1 1 1 1 d Dxy xy x x y − −− y = − ∫∫ i 2 2 1 d d 1 Dxy x x y y − = − ∫∫ 2 2 π 1 2 0 0 1 d θ d 1 h ρ ρ ρ − = − ∫ ∫ = − 2 π ln h

例2计算曲面积分 ∯02(x+y+za5, 其中∑是由平面x=0,y=0,z=0 及x+y+z=1所围成的四面体的整 个边界曲面(如右图). 解:整个边界曲面∑在平面x=0,y=0,z=0及 x+y+z=1上的部分分别记为21,22,及∑4:于是, ∯2(+y+zas =xy(x+y+=)ds+x=(x+y+)dS J∬z(x+y+z)ds+∬z(x+y+z)ds 2009年7月27日星期一 9 目录 上页 下页 返回
2009年7月27日星期一 9 目录 上页 下页 返回 例 2 计算曲面积分 xyz x( )d y z S Σ + + w∫∫ , 其中 Σ 是由平面 x = 0 ,y = 0 ,z = 0 及 x + y z + = 1所围成的四面体的整 个边界曲面(如右图). 解:整个边界曲面 Σ 在平面 x = 0 , y = 0 , z = 0 及 x ++= y z 1上的部分分别记为 Σ1,Σ 2 ,Σ 3 及 Σ 4 . 于是, xyz x y z S ( )d Σ + + w∫∫ 1 xyz x y z S ( )d Σ = ++ ∫∫ 2 xyz x y z S ( )d Σ + ++ ∫∫ 3 xyz x y z S ( )d Σ + ++ ∫∫ 4 xyz x y z S ( )d Σ + ++ ∫∫

注意到在2、∑2、∑,上,被积函数 f(x,y,z)=xyz(x+y+z) 都等于零因此有 )dS-+ds-(+dS-0 在∑4上,z=1-x-y, V1+zx2(x,)+z,2(x,y)=V1+(-1)2+(-12=3, 从而 ∯z(x+y+ds=j(x+y+2ds =J∬L-x-yXx+y+1-x-y小N3ddy=5 120 2009年7月27日星期一 10 目录 上页 下页 返回
2009年7月27日星期一 10 目录 上页 下页 返回 注意到在 Σ1﹑ Σ 2 ﹑ Σ 3 上,被积函数 f xyz y () ) , ( , = xyz x z + + 都等于 零.因此有 123 xyz x y z S xyz x y z S xyz x y z S ( )d ( ) ( d ) d 0 ΣΣΣ + + = ++ = ++ = ∫∫ ∫∫ ∫∫ 在 Σ 4 上, z =− − 1 x y , 2 2 1 (, ) (, ) x y + + z xy z xy 2 2 = +− +− 1 ( 1) ( 1) = 3 , 从而 xyz x y z S ( )d Σ + + w∫∫ 4 xy x y z z ( ) d S Σ = ++ ∫∫ (1 ) 1 ( ) 3 d d Dxy = xy x − −xy x + +y − − y x y ∫∫ 3 120 =