
数学模型 第四章 数学规划与数学模型 线性规划为运筹学的一个重要分支,应用很广,他研究的 问题主要包括两方面: 一 是任务确定后,如何以最低限度和成本(如人力、物力 、资金时间等),去完成任务。 二是如何在有限的条件下进行安排,以完成更多工作。 因此线性规划就是求一组变量的值,使要满足一组线性 式子并使一个线性函数的值最大(或最小)的数学方法
第四章 数学规划与数学模型 y 线性规划为运筹学的一个重要分支,应用很广,他研究的 问题主要包括两方面: 一是任务确定后,如何以最低限度和成本(如人力、物力 、资金时间等),去完成任务。 二是如何在有限的条件下进行安排,以完成更多工作。 因此线性规划就是求一组变量的值,使要满足一组线性 式子并使一个线性函数的值最大(或最小)的数学方法

数学模型 线性规划问题 建立线性规划模型是解决线性规划问 题等一个重要步骤。 建立的线性规划数学模型是否真正 的反应客观实际,数学模型本身是否正确, 都直接影响求解结果,从而影响决策结果, 所以,建立正确的线性规划模型尤为重要, 下面举例说明线性规划数学模型的建立
线 性 规 划 问 题 建立线性规划模型是解决线性规划问 题等一个重要步骤。 建立的线性规划数学模型是否真正 的反应客观实际,数学模型本身是否正确, 都直接影响求解结果,从而影响决策结果, 所以,建立正确的线性规划模型尤为重要, 下面举例说明线性规划数学模型的建立

致学模型 线性规划问题 建立线性规划模型是解决线性规划问题等一个重要步骤。 ·线性规划实例 生产计划问题 运输问题 ·线性规划模型 一般形式 规范形式 标准形式 形式转换 概念
线 性 规 划 问 题 • 线性规划实例 生产计划问题 运输问题 • 线性规划模型 一般形式 规范形式 标准形式 形式转换 概念 建立线性规划模型是解决线性规划问题等一个重要步骤
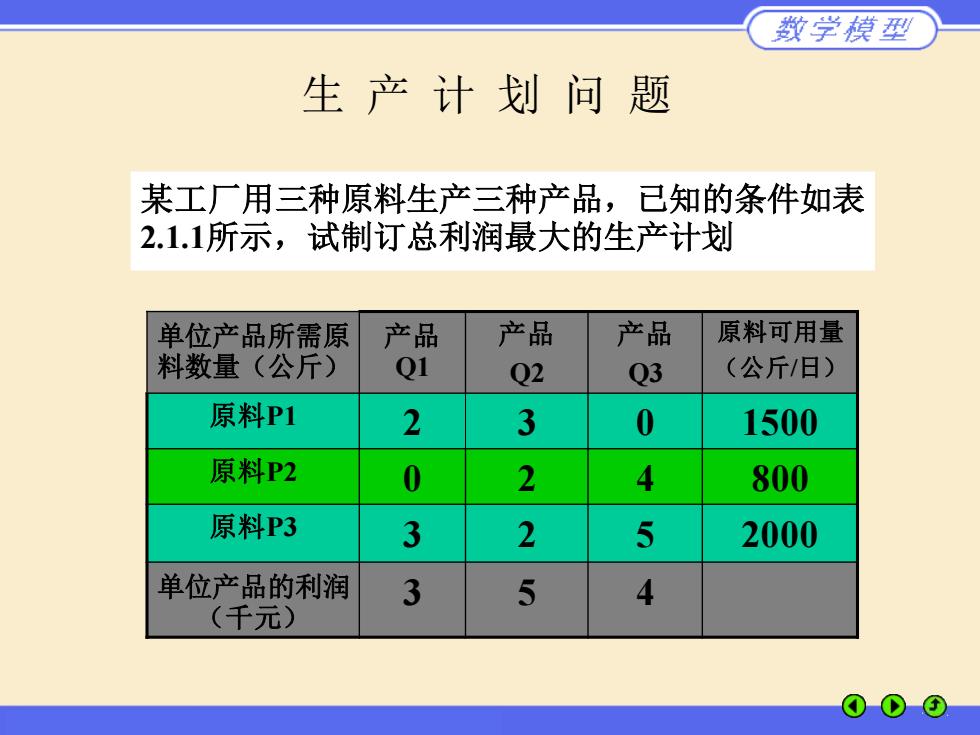
数学模型 生产计划问题 某工厂用三种原料生产三种产品,已知的条件如表 2.1.1所示,试制订总利润最大的生产计划 单位产品所需原 产品 产品 产品 原料可用量 料数量(公斤) Q1 Q2 Q3 (公斤/日) 原料P1 2 3 0 1500 原料P2 0 2 4 800 原料P3 3 2 5 2000 单位产品的利润 3 5 4 (千元)
某工厂用三种原料生产三种产品,已知的条件如表 2.1.1所示,试制订总利润最大的生产计划 单位产品所需原 料数量(公斤) 产品 Q1 产品 Q2 产品 Q3 原料可用量 (公斤/日) 原料P1 2 3 0 1500 原料P2 0 2 4 800 原料P3 3 2 5 2000 单位产品的利润 (千元) 3 5 4 生 产 计 划 问 题

数学模型 提出三个问题大家考虑: 1.问题的未知数是什么? 2.以什么准则进行决策? 3.约束条件是什么?
提出三个问题大家考虑: 1.问题的未知数是什么? 2.以什么准则进行决策? 3.约束条件是什么?
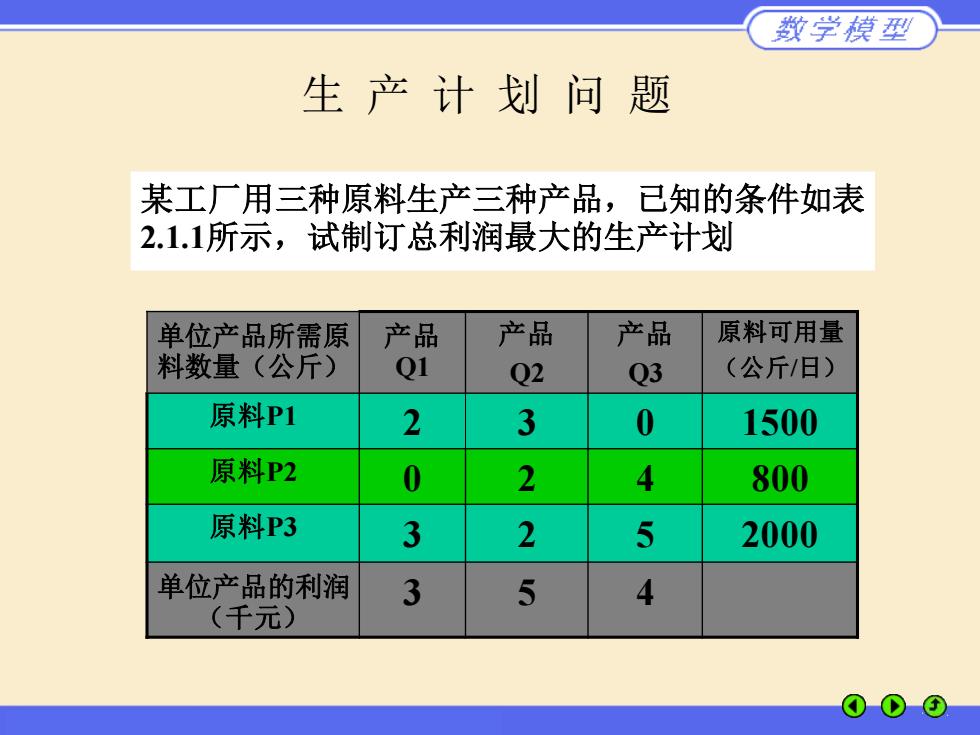
数学模型 生产计划问题 某工厂用三种原料生产三种产品,已知的条件如表 2.1.1所示,试制订总利润最大的生产计划 单位产品所需原 产品 产品 产品 原料可用量 料数量(公斤) Q1 Q2 Q3 (公斤/日) 原料P1 2 3 0 1500 原料P2 0 2 4 800 原料P3 3 2 5 2000 单位产品的利润 3 5 4 (千元)
某工厂用三种原料生产三种产品,已知的条件如表 2.1.1所示,试制订总利润最大的生产计划 单位产品所需原 料数量(公斤) 产品 Q1 产品 Q2 产品 Q3 原料可用量 (公斤/日) 原料P1 2 3 0 1500 原料P2 0 2 4 800 原料P3 3 2 5 2000 单位产品的利润 (千元) 3 5 4 生 产 计 划 问 题
数学模型 提出三个问题大家考虑: 1.问题的未知数是什么?二→设未知数 2.以什么准则进行决策?→ 目标函数 3.约束条件是什么?→约束方程
提出三个问题大家考虑: 1.问题的未知数是什么? 设未知数 2.以什么准则进行决策? 目标函数 3.约束条件是什么? 约束方程

数学模型 问题分析 可控因素:每天生产三种产品的数量,分别设为x,x2x 目标:每天的生产利润最大 利润函数3x,+5x2+4x 受制条件: 每天原料的需求量不超过可用量: 原料:2x1+3x2≤1500 原料P:2x2+4x3≤800 原料卫:3x1+2x2+5x3≤2000 蕴含约束:产量为非负数 x1,x2,x3≥0
问 题 分 析 可控因素:每天生产三种产品的数量,分别设为 1 2 3 x , x , x 目标:每天的生产利润最大 利润函数 1 2 3 3x + 5x + 4x 受制条件: 每天原料的需求量不超过可用量: 原料P1 :2x1 + 3x2 1500 原料 P2 :2 4 800 x2 + x3 原料P3 :3 2 5 2000 x1 + x2 + x3 蕴含约束:产量为非负数 x1 , x2 , x3 0

璥学模型 模型 max 3x+5x2+4x3 (2x1+3x2≤1500 S.t.2x2+4x3≤800 3x1+2x2+5x3≤2000 x1,x2,x3≥0
模 型 1 2 3 max 3x + 5x + 4x 2x1 + 3x2 1500 s.t. 2x2 + 4x3 800 3x1 + 2x2 + 5x3 2000 x1 , x2 , x3 0
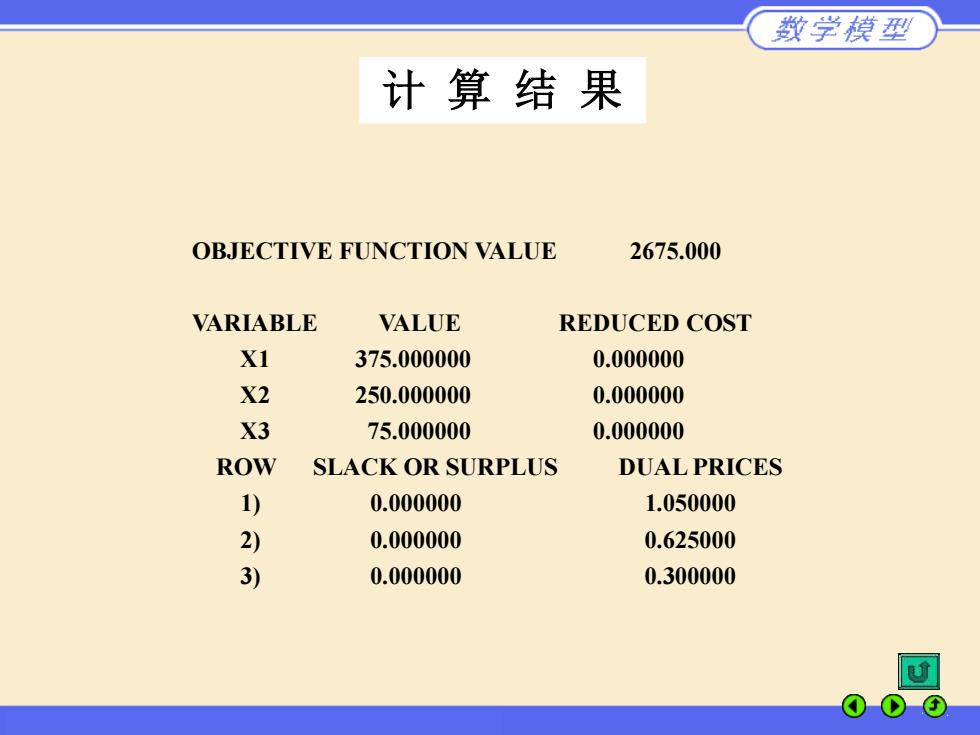
数学模型 计算结果 OBJECTIVE FUNCTION VALUE 2675.000 VARIABLE VALUE REDUCED COST XI 375.000000 0.000000 X2 250.000000 0.000000 X3 75.000000 0.000000 ROW SLACK OR SURPLUS DUAL PRICES 1) 0.000000 1.050000 2) 0.000000 0.625000 3) 0.000000 0.300000
计 算 结 果 OBJECTIVE FUNCTION VALUE 2675.000 VARIABLE VALUE REDUCED COST X1 375.000000 0.000000 X2 250.000000 0.000000 X3 75.000000 0.000000 ROW SLACK OR SURPLUS DUAL PRICES 1) 0.000000 1.050000 2) 0.000000 0.625000 3) 0.000000 0.300000