
线性方程徂的直接解法1 ·对称正定阵的分解定理 ·对称正定阵的分解公式 ·平方根法及改进的平方根法 ·三对角线性方程组的追赶法
线性方程组的直接解法1 • 对称正定阵的分解定理 • 对称正定阵的分解公式 • 平方根法及改进的平方根法 • 三对角线性方程组的追赶法

线性方程狙的直接解法巴 ·对称正定阵的分解定理 ·对称正定阵的分解公式 ·平方根法及改进的平方根法 ·三对角线性方程组的追赶法
线性方程组的直接解法2 • 对称正定阵的分解定理 • 对称正定阵的分解公式 • 平方根法及改进的平方根法 • 三对角线性方程组的追赶法

定理2.1(用紧凑格式解线性方程组的充分条件) 如果阶方阵A的各阶顺序主子式不为零,即 a,≠0, 0,.4≠0, a22 则方阵A必可作LU分解,且分解是唯一的。 定理2.2: 如果A为n阶对称方阵,且A的各阶顺序 主子式都不为零,则A可唯一分解为 A-LDL 其中L为单位下三角阵,D为对角阵
定理2.1(用紧凑格式解线性方程组的充分条件) 则方阵 必可作 分解,且分解是唯一的。 如果 阶方阵 的各阶顺序主子式不为零,即 A LU A a a a a a 0, 0, , 0, n A 2 1 2 2 1 1 1 2 1 1 定理2.2: 其中 为单位下三角阵, 为对角阵。 主子式都不为零,则 可唯一分解为 如果 为 阶对称方阵,且 的各阶顺序 D A LDL A A A T L n =
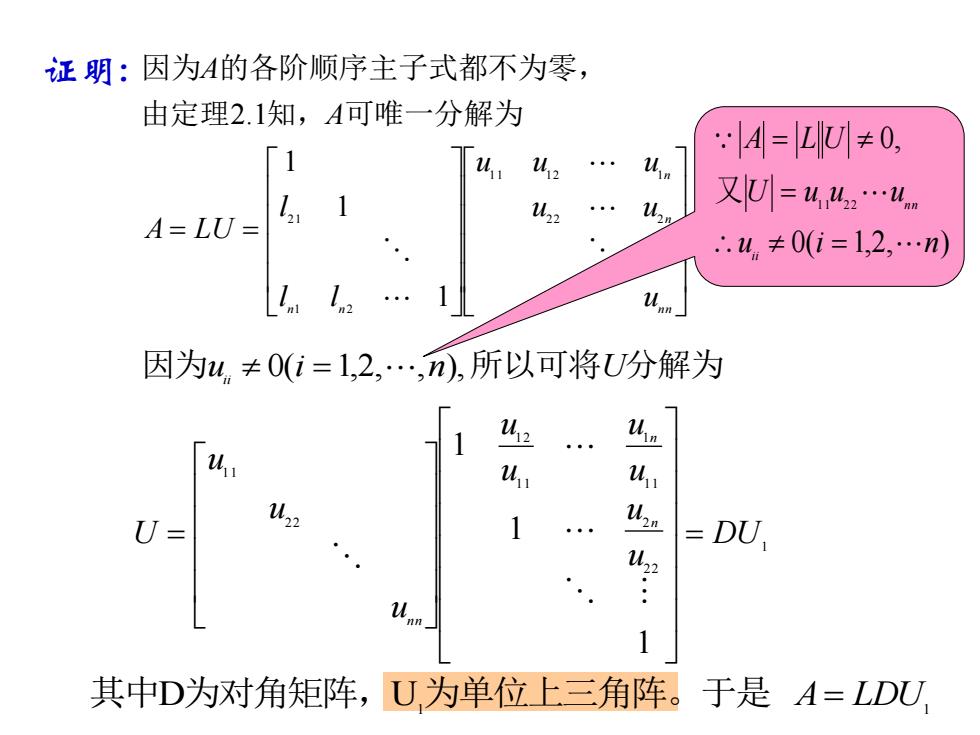
证明:因为A的各阶顺序主子式都不为零, 由定理2.1知,A可唯一分解为 1 4=LU≠0, u u, 又U=442.un A=LU= .u.≠0(i=1,2,.n) 1. 因为4.≠0(i=1,2,.,n),所以可将U分解为 2 DU 其中D为对角矩阵,U为单位上三角阵。于是A=LDU
= = n n n n n n u u u u u u l l l A LU A A 2 2 2 1 1 1 2 1 1 2 2 1 1 1 1 由定理2.1知, 可唯一分解为 证明: 因为 的各阶顺序主子式都不为零, 因为uii 0(i =1,2, ,n),所以可将U分解为 0( 1,2, ) 0, 1 1 2 2 u i n U u u u A L U ii n n = = = 又 其中D为对角矩阵,U1 为单位上三角阵。于是 A= LDU1 1 2 2 2 1 1 1 1 1 1 2 2 2 1 1 1 1 1 DU u u u u u u u u u U n n n n = =
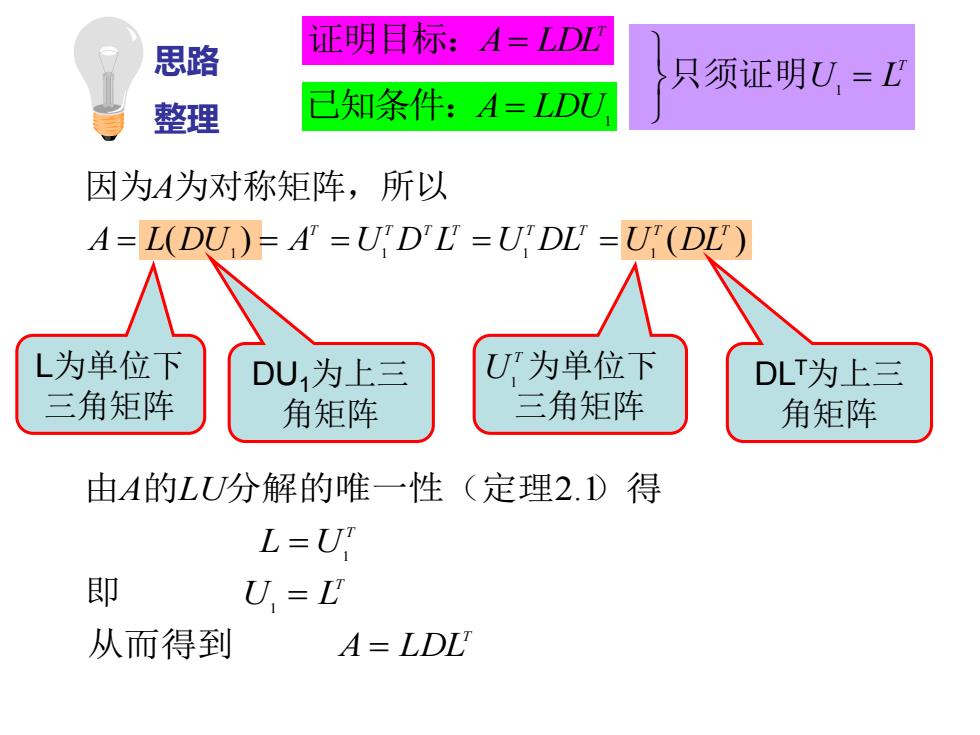
思路 证明目标:A=LDL 只须证明U= 整理 已知条件:A=LDU 因为A为对称矩阵,所以 A=L(DU )=A=UD'L=UDL =U(DL) L为单位下 DU1为上三 U”为单位下 DLT为上三 三角矩阵 角矩阵 三角矩阵 角矩阵 由A的LU分解的唯一性(定理2.D得 L=U' 即 U=L 从而得到 A-LDL
为单位下 三角矩阵 T U1 DLT为上三 角矩阵 L为单位下 三角矩阵 DU1为上三 角矩阵 ( ) ( ) 1 1 1 1 T T T T T T T T A L DU A U D L U DL U DL A = = = = = 因为 为对称矩阵,所以 T T T A LDL U L L U A LU = = = 从而得到 即 由 的 分解的唯一性(定理 )得 1 1 2.1 已知条件:A= LDU1 T 证明目标:A= LDL T U = L 只须证明 1 思路 整理
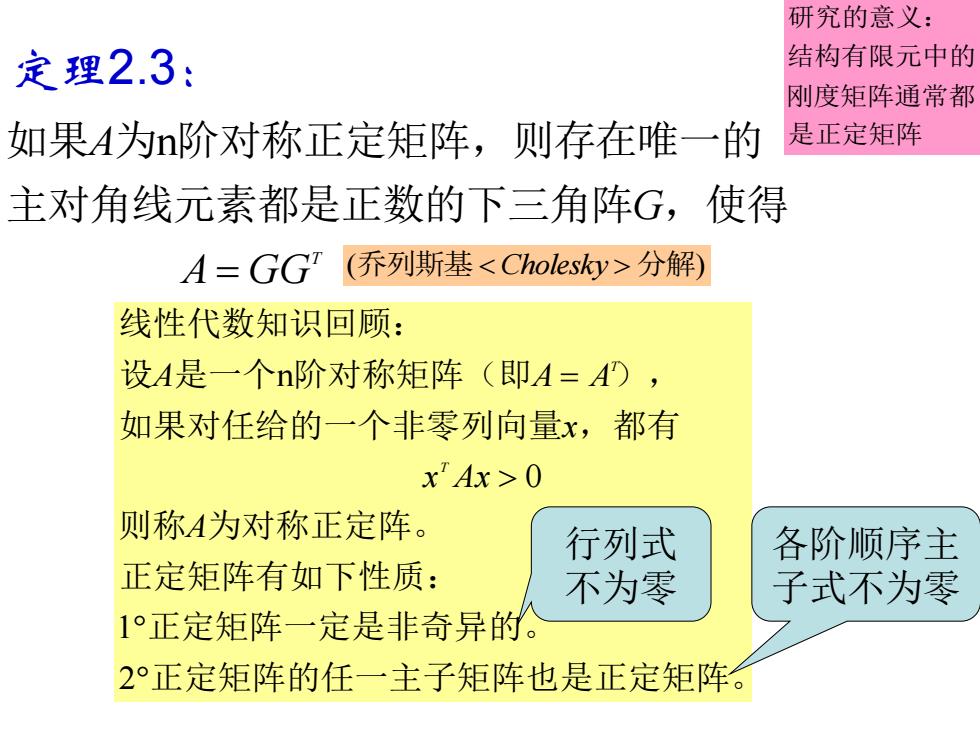
研究的意义: 定理2.3: 结构有限元中的 刚度矩阵通常都 如果A为n阶对称正定矩阵,则存在唯一的 是正定矩阵 主对角线元素都是正数的下三角阵G,使得 A=GGT(乔列斯基分解) 线性代数知识回顾: 设A是一个n阶对称矩阵(即A=A), 如果对任给的一个非零列向量x,都有 x"Ax>0 则称A为对称正定阵。 行列式 各阶顺序主 正定矩阵有如下性质: 不为零 子式不为零 1°正定矩阵一定是非奇异的。 2°正定矩阵的任一主子矩阵也是正定矩阵
定理2.3: T A GG G A = 主对角线元素都是正数的下三角阵 ,使得 如果 为n阶对称正定矩阵,则存在唯一的 正定矩阵的任一主子矩阵也是正定矩阵。 正定矩阵一定是非奇异的。 正定矩阵有如下性质: 则称 为对称正定阵。 如果对任给的一个非零列向量 ,都有 设 是一个 阶对称矩阵(即 ), 线性代数知识回顾: = 2 1 0 n A x Ax x A A A T T 是正定矩阵 刚度矩阵通常都 结构有限元中的 研究的意义: 行列式 不为零 各阶顺序主 子式不为零 (乔列斯基Cholesky 分解)

证明:A为对称正定矩阵 .A的各阶顺序主子式不为零(正定矩阵性质) ·.存在唯一的单位下三角阵L和对角阵D,使得 A=LDL' (定理2.2) 思路 整理 要证明A=GG,其中G为下三角矩阵 注意到: L乘以对角阵可获得下三角矩阵; 并且对角阵乘以可获得上三角矩阵。 因此,当D=M(M同样为对角阵)时, 则可令G=LM,于是 结论: 只需证明 G=(LM)=M'L=ML DE忙tm A=LDL'LMML=(LMML)=GG
= n n n n n n l d l d d l d d d d d d l l l 1 1 2 2 2 1 1 2 1 2 1 1 2 2 1 1 1 1 证明: T L A A A LDL D = 存在唯一的单位下三角阵 和对角阵 ,使得 的各阶顺序主子式不为零 为对称正定矩阵 (正定矩阵性质) (定理2.2) 思路 整理 要证明A= GGT ,其中G为下三角矩阵 乘以对角阵可获得下三角矩阵; 注意到 L : ( ) ( )( ) T T T T T T T T A LDL LMML LM ML G G LM M L ML = = = = = = = = = T 2 G G LM, D M M 则可令 于是 因此,当 ( 同样为对角阵)时, 并且对角阵乘以L T 可获得上三角矩阵。 结论: 只需证明 D=M2
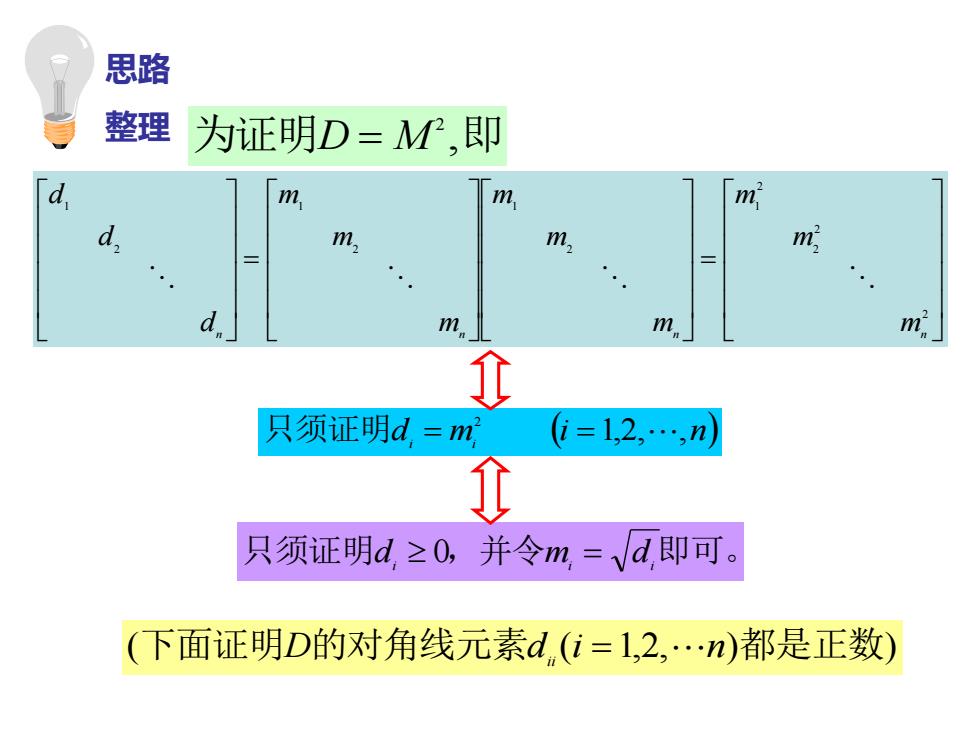
思路 整理 为证明D=P,即 0 m m m d m, m, m m. m 只须证明d=m i=1,2,.,n 只须证明d≥0,并令m=√d即可。 (下面证明D的对角线元素d(i=1,2,.n)都是正数)
思路 整理 = = 2 2 2 2 1 2 1 2 1 2 1 n n n mn m m m m m m m m d d d 为证明D = M 2 ,即 d m (i n) i i 1,2, , 只须证明 = 2 = 只须证明di 0,并令mi = di即可。 (下面证明D的对角线元素d (i 1,2, n)都是正数) ii =

(下面证明D的对角线元素d,(i=1,2,.n)都是正数) 由于L'非奇异,所以存在一非零向量x,使得Lx=e,其中 e为n阶单位矩阵中的第i个列向量。 由A的正定性可得 0<x"Ax =x'(LDL)x =x'LDL'x =(I'x)'DL'x =e'De,=d (i=1,2,.,n) 用M表示对角元素为/d(i=1,2,.,n)的对角阵,则有D=MP 令G=LM,则有 A-LDL =L(MM)L-(LM)LM)=GG 其中G为对角元素都是正数的下三角阵
(下面证明D的对角线元素d (i 1,2, n)都是正数) ii = 为 阶单位矩阵中的第 个列向量。 由于 非奇异,所以存在一非零向量 ,使得 ,其中 e n i L x L x e i i T T = ( )( ) 其中 为对角元素都是正数的下三角阵。 令 ,则有 G A LDL L MM L LM LM G G G LM T T T T = = = = = ( ) 2 用M表示对角元素为 dii (i =1,2, ,n)的对角阵,则有D = M ( 1,2, , ) 0 ( ) ( ) i n x Ax x LDL x x LDL x L x DL x e De d A i ii T i T T T T T T T T = = = = = = 由 的正定性可得

线性方程组的直接解法1 ·对称正定阵的分解定理 ·对称正定阵的分解公式 ·平方根法及改进的平方根法 ·三对角线性方程组的追赶法
线性方程组的直接解法1 • 对称正定阵的分解定理 • 对称正定阵的分解公式 • 平方根法及改进的平方根法 • 三对角线性方程组的追赶法