
线性方程狙的直接解法1 ·高斯消去法 ·列主元消去法 ·LU分解
线性方程组的直接解法1 • 高斯消去法 • 列主元消去法 • LU分解

线性方程组的直接解法1 ·高斯消去法 ·列主元消去法 ·LU分解
线性方程组的直接解法1 • 高斯消去法 • 列主元消去法 • LU分解
我们知道,下面有3种方程的解我们可以直接求出: 0=加g(aa,a)→x=,=lm n次运算 0 1- (n+1)/2次运算 ②A i=1 →X= -,i=1,.,n nn ⊙ (n十1)n/2次运算 212 6-∑4,x 1W22 u2n →X= j=i+1 ,i=n,.,1 u
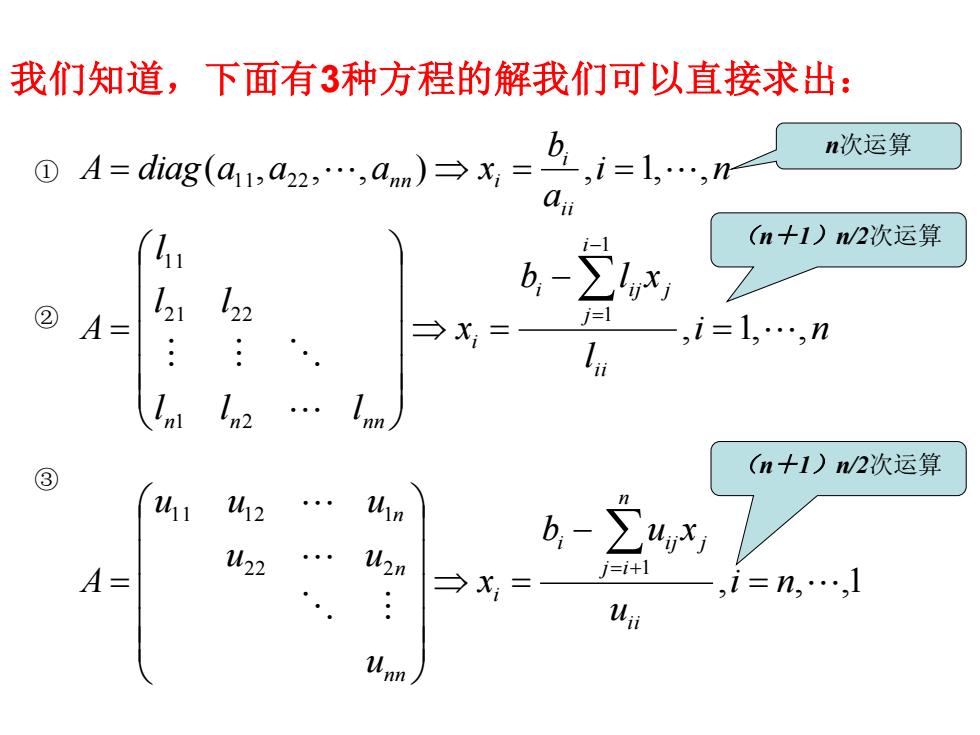
我们知道,下面有3种方程的解我们可以直接求出: i n a b A diag a a a x i i i n n i ( , , , ) , 1, , ① = 1 1 2 2 = = n次运算 i n l b l x x l l l l l l A i i i j i i j j i n n n n , 1, , 1 1 1 2 2 1 2 2 1 1 = − = = − ② = (n+1)n/2次运算 , , ,1 2 2 2 1 1 1 1 2 1 i n u b u x x u u u u u u A i i n j i i i j j i n n n n = − = = = + ③ (n+1)n/2次运算

对线性方程组作如下的变换,解不变: ①交换两个方程的次序 ②一个方程的两边同时乘以一个非0的数 ③一个方程的两边同时乘以一个非0数,加到另一个方程 因此,增广矩阵A,b)作如下的变换,方程组的解不变 ①交换矩阵的两行 ②某一行乘以一个非0的数 ③某一个乘以一个非0数,加到另一行 消元法就是对增广矩阵作上述行的变换,变为我们已 知的3种类型之一,而后求根
对线性方程组作如下的变换,解不变: ①交换两个方程的次序 ②一个方程的两边同时乘以一个非0的数 ③一个方程的两边同时乘以一个非0数,加到另一个方程 因此,增广矩阵(A,b) 作如下的变换,方程组的解不变 ①交换矩阵的两行 ②某一行乘以一个非0的数 ③某一个乘以一个非0数,加到另一行 消元法就是对增广矩阵作上述行的变换,变为我们已 知的3种类型之一,而后求根
高斯消去法:或叫高斯消元法,是一个古老的求解线性方 程组的直接法。 思首先通过消元将4化为上三角阵,再回代求解 路 a a 0 a a12 . 0 a品 b2 a2 22 02m 0 0 a a a a,2 b 0 0 0 b
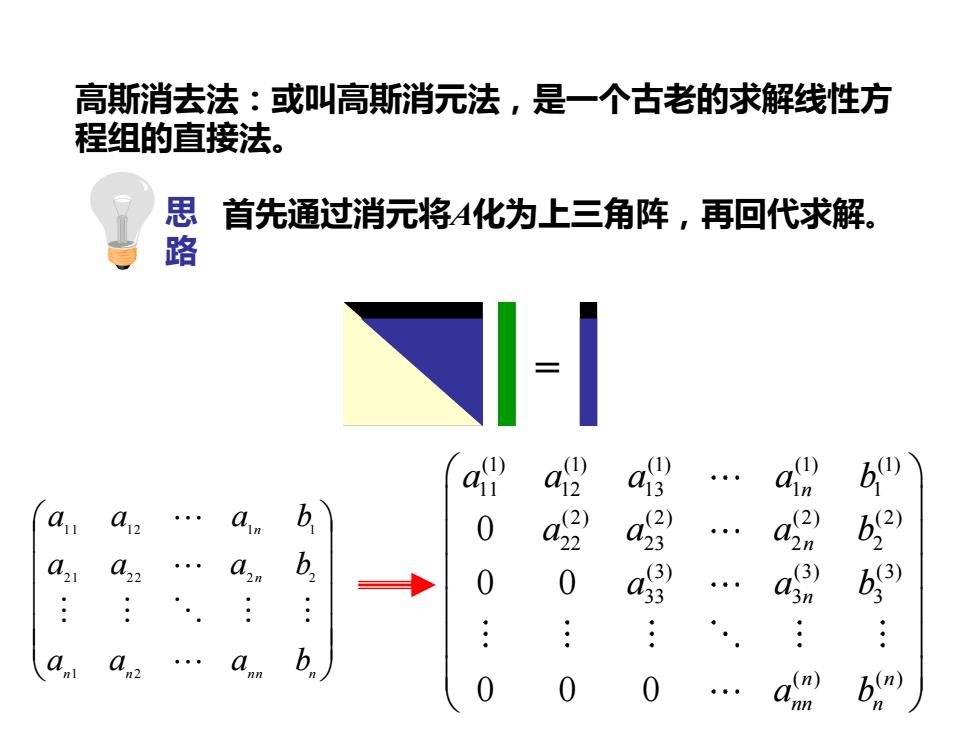
高斯消去法:或叫高斯消元法,是一个古老的求解线性方 程组的直接法。 n n n n n n n a a a b a a a b a a a b 1 2 2 1 2 2 2 2 1 1 1 2 1 1 (1) (1) (1) (1) (1) 11 12 13 1 1 (2) (2) (2) (2) 22 23 2 2 (3) (3) (3) 33 3 3 ( ) ( ) 0 0 0 0 0 0 n n n n n nn n a a a a b a a a b a a b a b 思 路 首先通过消元将A化为上三角阵,再回代求解。 =

高斯顺序消元法步骤如下: 第一步:当a,≠0,第1行×a+第行,i=2,n a11 12 n a21 22 a2n b2 0 a a b92 : an an2 0 a nn 第二步:当a≠0,第2行×二 i 2+第i行,i=3,.,n 22 b 12 b a 012 13 0 a 0 b2) a 0 0 a : : : a nn n 0 a用 a b
高斯顺序消元法步骤如下: 第一步: i i n a a a i 0, 1 , 2, , 1 1 1 1 1 + = − 当 第 行 第 行 n n n n n n n a a a b a a a b a a a b 1 2 2 1 2 2 2 2 1 1 1 2 1 1 (2) (2) (2) 2 (2) 2 (2) 2 (2) 22 11 12 1 1 0 0 n n n n n n a a b a a b a a a b 第二步: i i n a a a i 0, 2 , 3, , ( 2 ) 2 2 ( 2) ( 2 ) 2 2 2 + = − 当 第 行 第 行 (3) (3) (3) 3 (3) 3 (3) 3 (3) 3 3 (2) 2 (2) 2 (2) 2 3 (2) 2 2 1 1 1 2 1 3 1 1 0 0 0 0 0 n n n n n n n a a b a a b a a a b a a a a b (2) (2) (2) 2 (2) 2 (2) 2 (2) 22 11 12 1 1 0 0 n n n n n n a a b a a b a a a b
类似的做下去,我们有: 第k步:当a≠0,第k行 主元一直在作分母 一1步以后,我们可以得到变换后的矩阵为: 12 13 2 2 22 23 A2n 33 a b3 : 0 (n 'nn 几个概念: 高斯消去法的消元过程、回代过程以及主元
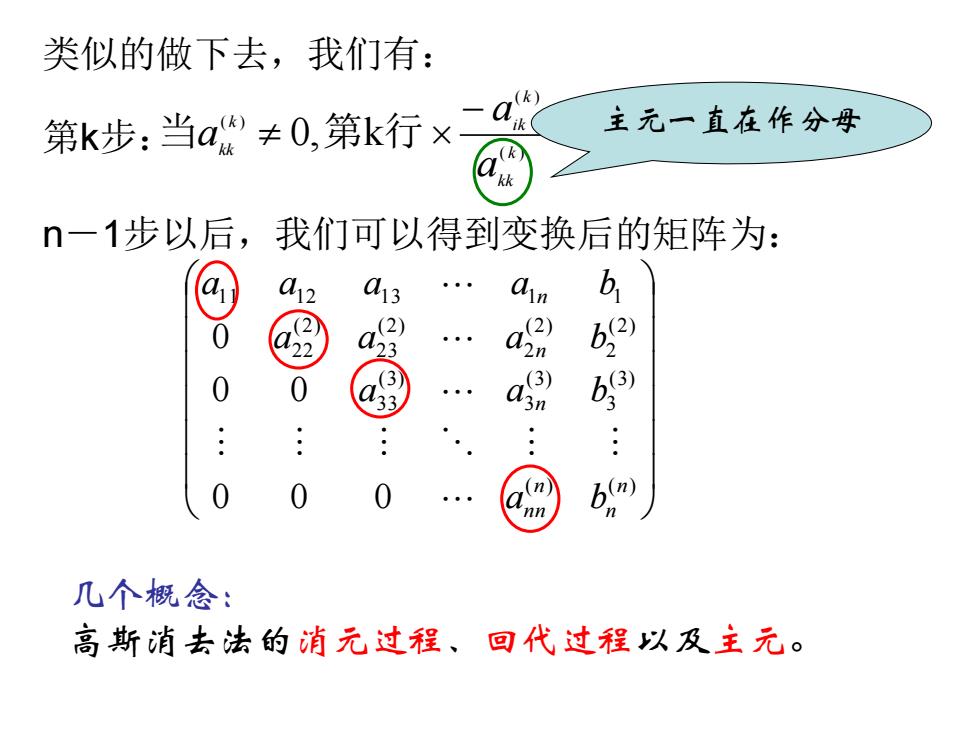
第k步: i i k n a a a k kk k k i k kk 0, k , 1, , ( ) ( ) ( ) + = + − 当 第 行 第 行 类似的做下去,我们有: ( ) ( ) (3) 3 (3) 3 (3) 3 3 (2) 2 (2) 2 (2) 2 3 (2) 2 2 1 1 1 2 1 3 1 1 0 0 0 0 0 0 n n n n n n n n a b a a b a a a b a a a a b n-1步以后,我们可以得到变换后的矩阵为: 几个概念: 高斯消去法的消元过程、回代过程以及主元。 主元一直在作分母

高斯消去法存在的问题: 1.Gauss?消元法的可行条件为:a≠0; 2.如果某个a很小的话,会引入较大的误差。 例1:单精度解方程组10x+x,=1 (1+x2=2 8个 8个 精确群为玉三10100000和x2-x=0,9989. 用Gaussian消元法计算:m!=a1/a,⑩个 大数吃小数 422=1-m21×1=0.0.01×109-109=-109 lb2=2-m21×1÷-10 1 1 0 -109 109 小主元可能导致计算 →x2=1,1€( 失败
高斯消去法存在的问题: 2. 如果某个 很小的话,会引入较大的误差。 (k ) kk a 1.Gauss消元法的可行条件为: akk (k ) 0 ; 例1:单精度解方程组 + = + = − 2 10 1 1 2 1 2 9 x x x x /* 精确解为 1.00.0100. 和 */ 1 10 1 1 9 = − = − x 8个 2 0.99 . 9899. 2 1 x = − x = 8个 用Gaussian 消元法计算: 9 m21 = a21 / a11 = 10 9 9 9 a2 2 = 1− m2 1 1 = 0.0.0110 −10 = −10 8个 9 b2 = 2− m21 1 = −10 − − − 9 9 9 0 10 10 10 1 1 x2 =1, x1 = 0 小主元可能导致计算 失败。 大数吃小数

线性方程组的直接解法1 ·高斯消去法 ·列主元消去法 ·LU分解
线性方程组的直接解法1 • 高斯消去法 • 列主元消去法 • LU分解
高斯列主元消元法 在Gauss消元的第k步之前,首先选主元: 若 maxa曰aI且k≠j,交换k行和j行 k<i<n 12 挑选从第二行开始的第 二列中的最大元素,交换 0 行将其变为主元 22 ZI 以第二步为例: 2 n2 a 行的交换,不改变方程组的解,同时又有效地克 服了Gauss消元的缺陷 例: 10-9 L① → x2=1,x1=1
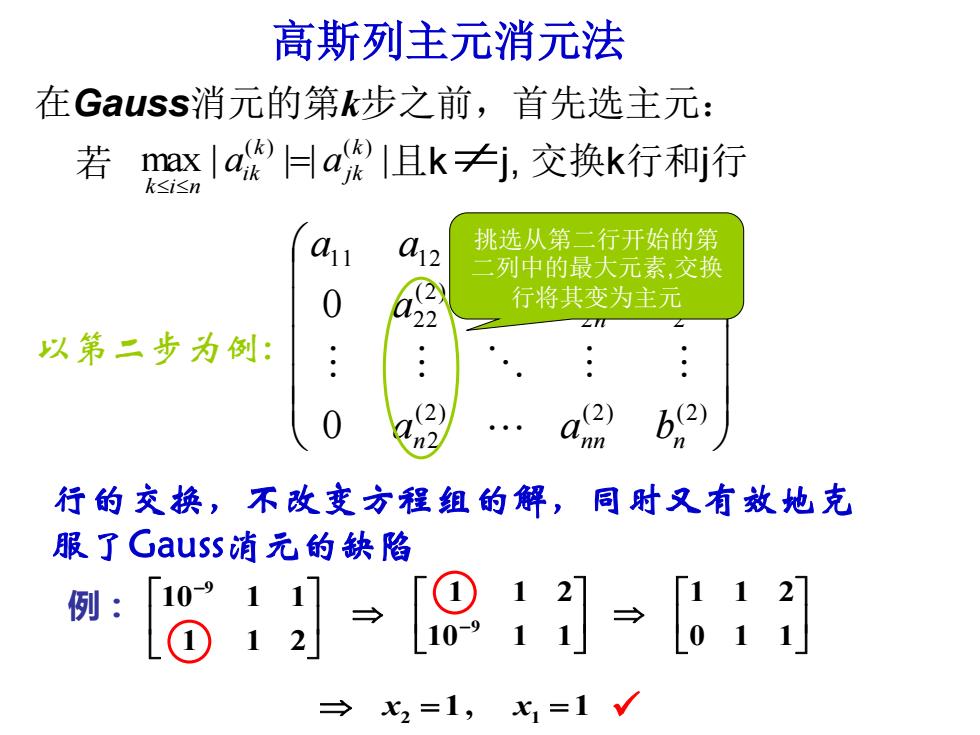
高斯列主元消元法 在Gauss消元的第k步之前,首先选主元: max | | | | ( ) (k ) jk k ik k i n a = a 若 且k j, 交换k行和j行 行的交换,不改变方程组的解,同时又有效地克 服了Gauss消元的缺陷 例: − 1 1 2 10 1 1 9 x2 = 1 , x1 = 1 0 1 1 1 1 2 − 10 1 1 1 1 2 9 ✓ (2) (2) (2) 2 (2) 2 (2) 2 (2) 2 2 1 1 1 2 1 1 0 0 n n n n n n a a b a a b a a a b 以第二步为例: 挑选从第二行开始的第 二列中的最大元素,交换 行将其变为主元