
线性方程组的送代解法 ·迭代法概述 。迭代法的构造 ·迭代法的分量形式 ·松弛法 ●迭代法的收敛性
线性方程组的迭代解法 • 迭代法概述 • 迭代法的构造 • 迭代法的分量形式 • 松弛法 • 迭代法的收敛性

线性方程狙的迭代解法 ·迭代法概述 ·迭代法的构造 ·送代法的分量形式 ●松弛法 ·迭代法的收敛性
线性方程组的迭代解法 • 迭代法概述 • 迭代法的构造 • 迭代法的分量形式 • 松弛法 • 迭代法的收敛性

求解线性方程组的两种基本方法 直接法比较适用于中小型方程组。对高阶方 程组,即使系数矩阵是稀疏的,但在运算中 很难保持稀疏性,因而有存储量大,程序复 杂等不足 迭代法则能保持矩阵的稀疏性,具有计算简 单,编制程序容易的优点,并在许多情况下 收敛较快。故能有效地解一些高阶方程组
直接法比较适用于中小型方程组。对高阶方 程组,即使系数矩阵是稀疏的,但在运算中 很难保持稀疏性,因而有存储量大,程序复 杂等不足. 迭代法则能保持矩阵的稀疏性,具有计算简 单,编制程序容易的优点,并在许多情况下 收敛较快。故能有效地解一些高阶方程组。 求解线性方程组的两种基本方法

将Ax=b等价改写为x=Bx+f形式,建立迭 思 路代=Bx+∫。从初值)出发,得到序列)} 迭代矩阵 若向量序列x}是收敛的,即Iimx=x, 或x=Bx+d,则x是Ax=b的解。 研究 内容: 如何建立迭代格式? 没收敛速度? 向量序列的收敛条件? 。误差估计?
思 路 将 等价改写为 形式,建立迭 代 。从初值 出发,得到序列 。 A x = b x = B x + f x B x f k k = + ( +1) ( ) ( 0) x { } ( k ) x 研究 内容: 如何建立迭代格式? 收敛速度? 向量序列的收敛条件? 误差估计? 或 ,则 是 的解。 若向量序列 是收敛的,即 , x Bx d x Ax b x x x k k k = + = = → * * * ( ) ( ) * { } lim 迭代矩阵

线性方程组的送代解法 。迭代法概述 ·迭代法的构造 ·送代法的分量形式 ·松弛法 ●迭代法的收敛性
线性方程组的迭代解法 • 迭代法概述 • 迭代法的构造 • 迭代法的分量形式 • 松弛法 • 迭代法的收敛性

令A=L+D+UU则(L+D+U)x=bA= 于是 1°Dr=b-LHOK比迭 矩阵 x=-D'(L年书b 公式:rm2u+)+Db 雅克比迭代 高斯-塞德 尔迭代矩阵 2°(L+D)x=b-Ux x=-(L+D)Ux+(L+D)b 公式2:x=-(L+D)'Ux+(L+D'b 高斯-塞德尔迭代
高斯-塞德尔迭代 雅克比迭代 雅克比迭 代矩阵 ( ) x (L D) Ux (L D) b L D x b Ux 1 1 0 2 − − = − + + + + = − A = L U 令A = L + D +U 则(L + D +U)x = b D ( ) x D (L U)x D b Dx b L U x 1 1 0 1 − − = − + + = − + 于是 x (L D) Ux (L D) b k k 1 ( ) 1 ( 1) 2 + − − 公式 : = − + + + x D L U x D b ( k 1) 1 (k ) 1 1 ( ) + − − 公式: = − + + 高斯-塞德 尔迭代矩阵

线性方程组的送代解法 。迭代法概述 。迭代法的构造 ·迭代法的分量形式 ·松弛法 ●迭代法的收敛性
线性方程组的迭代解法 • 迭代法概述 • 迭代法的构造 • 迭代法的分量形式 • 松弛法 • 迭代法的收敛性

雅克比迭代:x=-D[【(L+U)x- 相当于:Dx=[(L+U)x-b] ax"=-ax+ax++a.x-b) 即a,”=-+ax++ax-b (k+1) ax=-ax+ax+.+ax-b)
x D L U x b k k = − + − ( +1) −1 ( ) 雅克比迭代: ( ) Dx L U x b k k = − + − ( +1) ( ) 相当于: ( ) ( ) ( ) ( ) = − + + + − = − + + + − = − + + + − − − + + + n k n n n k n k n k n n n k n n k k k k n n k k k a x a x a x a x b a x a x a x a x b a x a x a x a x b ( ) 1 1 ( ) 2 2 ( ) 1 1 ( 1) 2 ( ) 1 ( ) 2 3 3 ( ) 2 1 1 ( 1) 2 2 2 1 ( ) 1 ( ) 1 3 3 ( ) 1 2 2 ( 1) 1 1 1 即
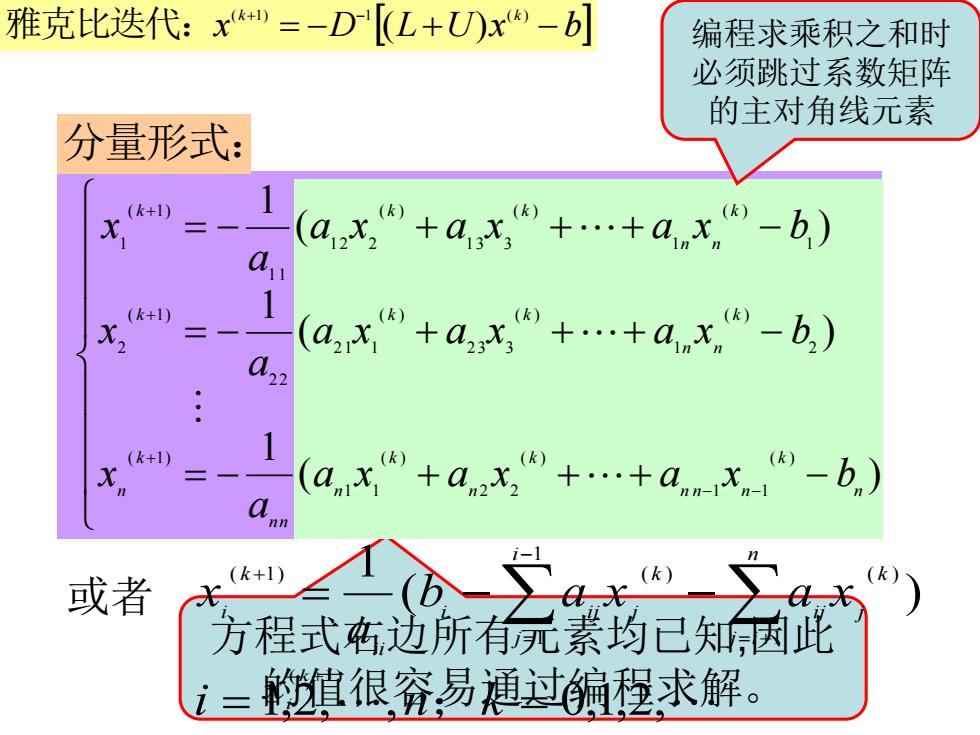
雅克比迭代:x=-D《L+U)x-b] 编程求乘积之和时 必须跳过系数矩阵 的主对角线元素 分量形式: (k+1) (ax+a,x+.+a,x-b) a (k+1) 1 X2 (.) 022 1 (k+1) (ax+ax+.+a.x,-b.) 或者 (k+1) 方程式名边所有元素均已知因此 i=進很穷易通过编程求解
方程式右边所有元素均已知,因此 的值很容易通过编程求解。 ( k +1) i x 编程求乘积之和时 必须跳过系数矩阵 的主对角线元素 = − + + + − = − + + + − = − + + + − − − + + + ( ) 1 ( ) 1 ( ) 1 ( ) 1 1 ( ) 2 2 ( ) 1 1 ( 1) 2 ( ) 1 ( ) 2 3 3 ( ) 2 1 1 2 2 ( 1) 2 1 ( ) 1 ( ) 1 3 3 ( ) 1 2 2 1 1 ( 1) 1 n k n n n k n k n n n k n k n n k k k k n n k k k a x a x a x b a x a x a x a x b a x a x a x a x b a x x D L U x b k k = − + − ( +1) −1 ( ) 雅克比迭代: ( ) 分量形式: 1,2,, 0,1,2, ( ) 1 1 ( ) 1 1 ( 1) ( ) = = = − − = + − = + i n k b a x a x a x n j i k i j j i j k i i j j i i k i ; 或者

雅可比迭代公式也可以写成以下形式: 两个一维数组对应 元素的乘积之和, 分量形式: 程序设计较为简单 x=(ad-b) (k+1) 1 X ()_ 二X21 (a,x+ax,+.+ax,-b,) 022 (k+1) =x-(ax+ax”++ax"-b) 或者 x"=x”+(6-2a,x")) i=12,.,n;k=0,1,2
两个一维数组对应 元素的乘积之和, 程序设计较为简单 = − + + + − = − + + + − = − + + + − + + + ( ) 1 ( ) 1 ( ) 1 ( ) ( ) 2 2 ( ) 1 1 ( 1) ( ) 2 ( ) 1 ( ) 2 2 2 ( ) 2 1 1 2 2 ( ) 2 ( 1) 2 1 ( ) 1 ( ) 1 2 2 ( ) 1 1 1 1 1 ( ) 1 ( 1) 1 n k n n n k n k n n n k n k n k n n k k k k k n n k k k k a x a x a x b a x x a x a x a x b a x x a x a x a x b a x x 雅可比迭代公式也可以写成以下形式: 1,2,, 0,1,2, ( ) 1 1 ( 1) ( ) ( ) = = = + −= + i n k b a x a x x n j k i ij j ii k i k i ; 或者 分量形式: