
西安电子科技大学离散数学软件学院第一篇数理逻辑第2章谓词逻辑V第7课时1.1谓词和量词第8课时A1.2谓词公式之第9课时1.3谓词公式的翻译→第10课时1.4谓词演算的永真公式第11课时1.5谓词演算的四个推理规则?第12课时1.6谓词逻辑推理及应用→
西安电子科技大学 离散数学 软件学院 第一篇 数理逻辑 第7课时 1.1 谓词和量词 第2章 谓词逻辑 1.4 谓词演算的永真公式 1.2 谓词公式 1.5 谓词演算的四个推理规则 第8课时 第10课时 第11课时 第9课时 1.3 谓词公式的翻译 第12课时 1.6 谓词逻辑推理及应用
西安电子科技大学S2.3.1个体域的选取软件学院变元的个体域会影响谓词公式的取值例如:设P(x):是草食动物,Ox):x是无性繁殖的论个体域D1:全体动物,D2:兔子(x) P()的含义(Vx) P(×)的真值FD1所有的动物都是食草动物TD2所有的兔子都食草动物(日x) Q(x)的含义(日x) Q(×)的真值TD1有些动物是无性繁殖的FD2有些兔子是无性繁殖的如果谓词公式中变元的个体域选取的不同,谓词公式的真值也可能随之不同
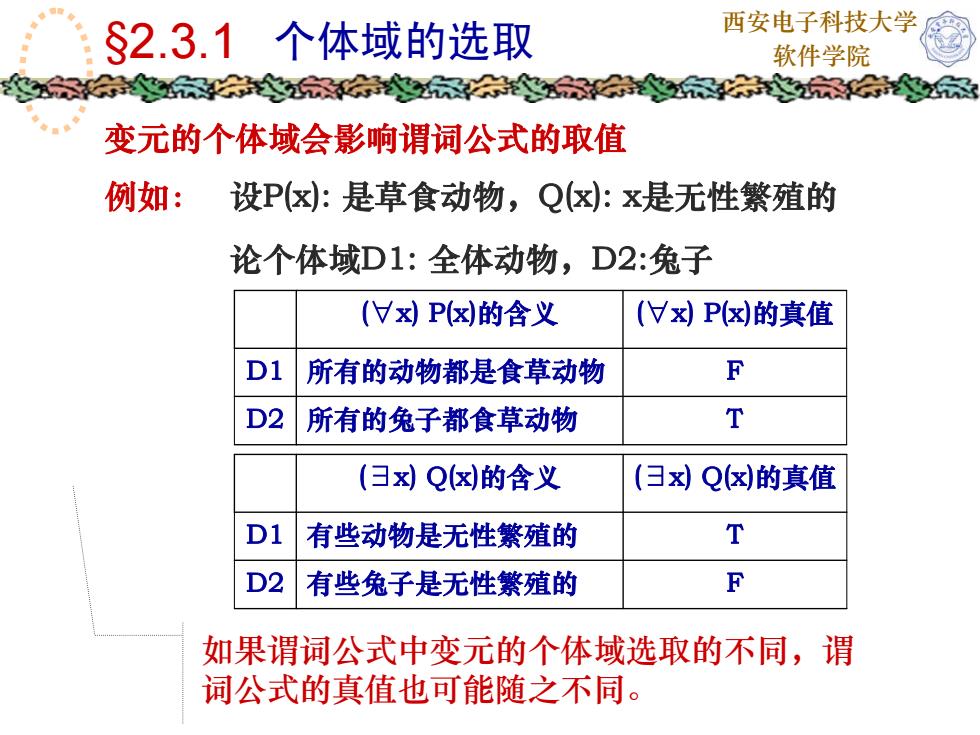
西安电子科技大学 §2.3.1 个体域的选取 软件学院 变元的个体域会影响谓词公式的取值 例如: 设P(x): 是草食动物,Q(x): x是无性繁殖的 论个体域D1: 全体动物,D2:兔子 (∀x) P(x)的含义 (∀x) P(x)的真值 D1 所有的动物都是食草动物 F D2 所有的兔子都食草动物 T (∃x) Q(x)的含义 (∃x) Q(x)的真值 D1 有些动物是无性繁殖的 T D2 有些兔子是无性繁殖的 F 如果谓词公式中变元的个体域选取的不同,谓 词公式的真值也可能随之不同

西安电子科技大学S2.3.1个体域的选取软件学院【例题】分别在变元论域D1=“全人类”和D=“全体动物”中,将以下语句翻译成谓词公式。(a)“所有人都是要死的”(b)“有些人不怕死”解答:设P(×):x是人,Q(x):x是要死的,R(x):x怕死(a)在个体域D1中的翻译为:(Vx)Q(x)在个体域D2中的翻译为:(Vx)(P(x)→Q(x)(b)在个体域D1中的翻译为:(日x)一Q(x)在个体域D2中的翻译为:(日x)(P(x)^-R(x))
西安电子科技大学 软件学院 (a)在个体域D1中的翻译为: ( ∀x)Q(x) 在个体域D2中的翻译为: ( ∀x)(P(x) →Q(x)) 解答: (b)在个体域D1中的翻译为: ( ∃x)¬ Q(x) 在个体域D2中的翻译为: ( ∃x)(P(x) ∧¬ R(x)) 设P(x): x是人,Q(x): x是要死的,R(x): x怕死 §2.3.1 个体域的选取
西安电子科技大学S2.3.1个体域的选取软件学院世界上所有的个体汇集在一起构成的集合。全总个体域为了方便和统一,通常将所有变元的个体域均指定为全总个体域
西安电子科技大学 软件学院 全总个体域 为了方便和统一,通常将所有变元的个体域 均指定为全总个体域。 §2.3.1 个体域的选取
西安电子科技大学$2.3.2特性谓词软件学院变元的论域统一取全总个体域后,变元所能取的个体范围都确定为所有可能的个体,但具体的命题讨论的往往是确定的一类对象,这样首先要将讨论的个体范围具体化,这就用到了特性谓词。P(×) :x是人特性谓词的作用是限定论域为一个满足该谓词的所有个体构成的一个特定的个体域0
西安电子科技大学 软件学院 变元的论域统一取全总个体域后,变元所能取的个体范围都 确定为所有可能的个体,但具体的命题讨论的往往是确定的 一类对象,这样首先要将讨论的个体范围具体化,这就用到 了特性谓词 。 P(x) :x是人 特性谓词的作用是限定论域为一个满足该谓词 的所有个体构成的一个特定的个体域 。 §2.3.2 特性谓词

西安电子科技大学$2.3.2特性谓词-软件学院家教家【例题】在全总个体域中将下些语句翻译成谓词公式。(a)所有的人都是要死的;(b)有些人不怕死。解答:设P(×):x是人,Q(×):x是要死的,R(x):x怕死(a) 翻译为:(Vx)(P()→Q(≤))(b) 翻译为:(日x)(P(x) ^-R(×)
西安电子科技大学 软件学院 (a)翻译为: (∀x)(P(x)→Q(x)) 解答: (b)翻译为: (∃x)(P(x)∧¬ R(x)) 设P(x): x是人,Q(x): x是要死的,R(x): x怕死 【例题】在全总个体域中将下些语句翻译成谓词公式。 (a)所有的人都是要死的; (b)有些人不怕死。 §2.3.2 特性谓词

西安电子科技大学$2.3.2特性谓词软件学院家家特性谓词的使用有以下两条规则:(1)对于全称量词,特性谓词应作为蕴含式的前件加入;(2)对于存在谓词,特性谓词作为合取项加入。对于特性谓词,如果被全称量词量化其后用一→,如果被存在量词量化其后用Λ
西安电子科技大学 软件学院 对于特性谓词,如果被全称量词量化其 后用→,如果被存在量词量化其后用 ∧ 。 §2.3.2 特性谓词

西安电子科技大学$2.3.3谓词公式的翻译软件学院家教家【例题】在全总个体域中将下些语句翻译成谓词公式。(a)每个有理数都是实数:(b)实数不都是有理数(有些实数不是有理数)解答:设R(≤):x是实数,Q(x):x是有理数(a) 翻译为: (Vx)(Q()→R(×)或(b) 翻译为: -( x)(R(×)→Q(≤)(x)(R() Λ Q(×)
西安电子科技大学 §2.3.3 谓词公式的翻译 软件学院 【例题】在全总个体域中将下些语句翻译成谓词公式。 (a)每个有理数都是实数; (b)实数不都是有理数(有些实数不是有理数)。 (a)翻译为: ( ∀x)(Q(x) → R(x)) 解答: (b)翻译为: ¬( ∀ x)(R(x) →Q(x)) 设R(x): x是实数,Q(x): x是有理数 ( ∃x)(R(x) ∧¬Q(x)) 或

西安电子科技大学$2.3.3谓词公式的翻译软件学院家【例题】判断下列命题是否等价。(a)金子都是闪光的;(b)没有不闪光的金子;(c)闪光的不都是金子;(d)有些东西虽然闪光但不是金子。(a)←(b)(c)(d)解答:仁在进行谓词公式翻译时,可以将命题转化为与之等价的另一个命题然后翻译,但要确保两者是等价的
西安电子科技大学 §2.3.3 谓词公式的翻译 软件学院 【例题】判断下列命题是否等价。 (a)金子都是闪光的; (b)没有不闪光的金子; (c)闪光的不都是金子; (d)有些东西虽然闪光但不是金子。 解答:(a) ⇔ (b) (c) ⇔ (d) 在进行谓词公式翻译时,可以将命题转化为 与之等价的另一个命题然后翻译,但要确保 两者是等价的

西安电子科技大学S2.3.3谓词公式的翻译软件学院家教家【例题】在全总个体域中将下些语句翻译成谓词公式(a)每个实数都有大于该实数的实数;(b)没有最大的实数。解答:设R(×):x是实数,L(x,y):x>y(a) 翻译为: (Vx)(R(x)→(y)(R(×) ^L(y,x))(b) 翻译为: -(x)(R() ^(Vy)( R(y)→L(区,y)因为(a)(b)这两个命题是等价的,所以:(Vx)(R(×)→ (y)( R(x) ^L(y,x) <)-(x)(R(x) ^ (Vy)(R(y)-L(区,y)
西安电子科技大学 §2.3.3 谓词公式的翻译 软件学院 【例题】在全总个体域中将下些语句翻译成谓词公式。 (a)每个实数都有大于该实数的实数; (b)没有最大的实数。 (a)翻译为: ( ∀x)(R(x) → ( ∃y)( R(x) ∧L(y,x)) 解答: (b)翻译为: ¬( ∃x)(R(x) ∧ ( ∀y)( R(y) →L(x,y)) 设R(x): x是实数,L(x,y): x>y 因为(a)(b)这两个命题是等价的,所以: ( ∀x)(R(x) → ( ∃y)( R(x) ∧L(y,x)) ¬( ∃x)(R(x) ∧ ( ∀y)( R(y) →L(x,y)) ⇔