西安电子科技大学离散数学软件学院第四篇图论第6章图论第27-28课时6.1图的基本概念-第29课时6.2路径与回路之第30课时6.3图的矩阵表示A第31课时6.4欧拉图与汉密尔顿图(1)A第33课时6.5平面图第34课时6.6图的着色6.7 树第35-36课时第37-38课时26.8图的应用
西安电子科技大学 离散数学 软件学院 第四篇 图论 6.1 图的基本概念 第6章 图论 6.4 欧拉图与汉密尔顿图(1) 6.2 路径与回路 6.5 平面图 第29课时 第33课时 第30课时 6.3 图的矩阵表示 第34课时 6.6 图的着色 第31课时 第35-36课时 6.7 树 第27-28课时 第37-38课时 6.8 图的应用
西安电子科技大学欧拉图----序言软件学院17世纪,东普鲁士,哥尼斯堡城,城中有一座奈佛夫岛普雷格尔河的两条支流环绕其旁,并将整个城市分为北区、东区、南区和岛区四个区域,全城共有7座桥将4个城区相连起来,人们常通过这7座桥到各城区游玩。哥尼斯堡七桥问题日
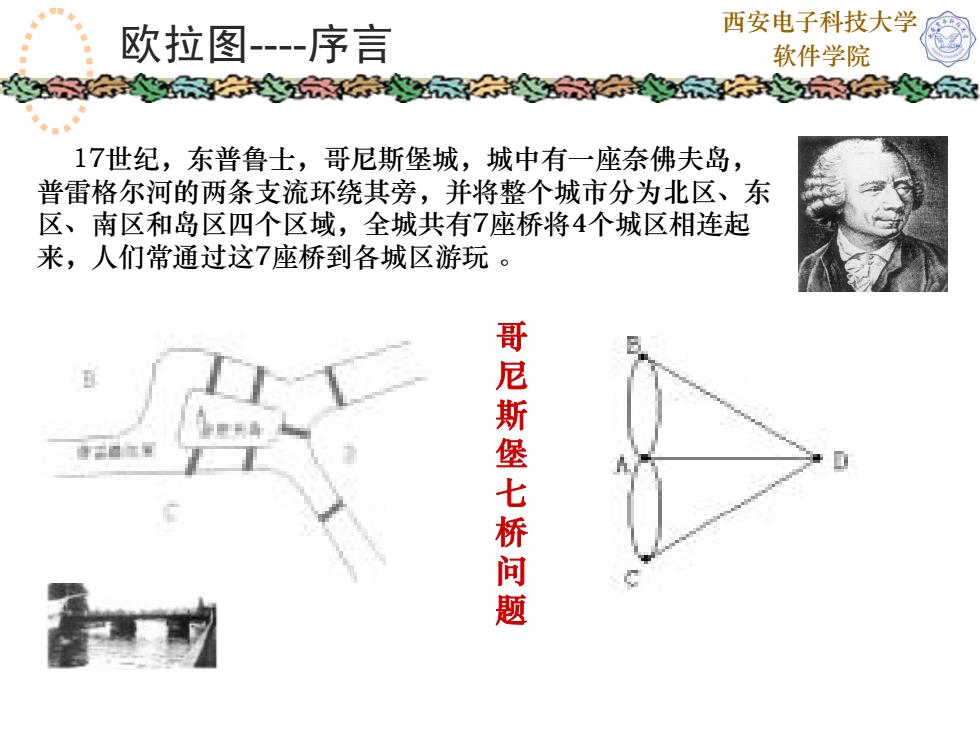
西安电子科技大学 软件学院 17世纪,东普鲁士,哥尼斯堡城,城中有一座奈佛夫岛, 普雷格尔河的两条支流环绕其旁,并将整个城市分为北区、东 区、南区和岛区四个区域,全城共有7座桥将4个城区相连起 来,人们常通过这7座桥到各城区游玩 。 哥 尼 斯 堡 七 桥 问 题 欧拉图-序言
西安电子科技大学欧拉图$6.4.1软件学院经过图G=中的每条边一次且仅一次的路径。欧拉路径V1V.V条欧拉路径:(V4,V3,V2,V4,V5,V2,V1,V3,V5)
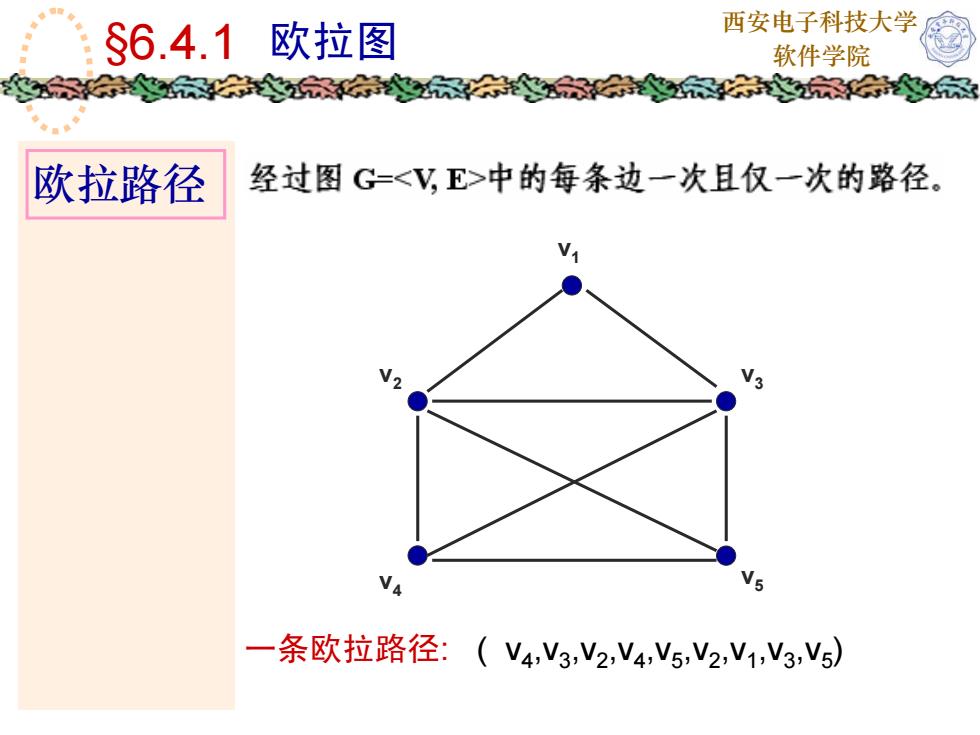
西安电子科技大学 欧拉图 软件学院 欧拉路径 §6.4.1 v1 v2 v3 v4 v5 一条欧拉路径: ( v4 ,v3 ,v2 ,v4 ,v5 ,v2 ,v1 ,v3 ,v5 )
西安电子科技大学欧拉图$6.4.1软件学院经过图G=中的每条边一次且仅一次的回路。欧拉回路VVV5V条欧拉回路:(V4,V3,V2,V5,V3,V1,V2,V4)
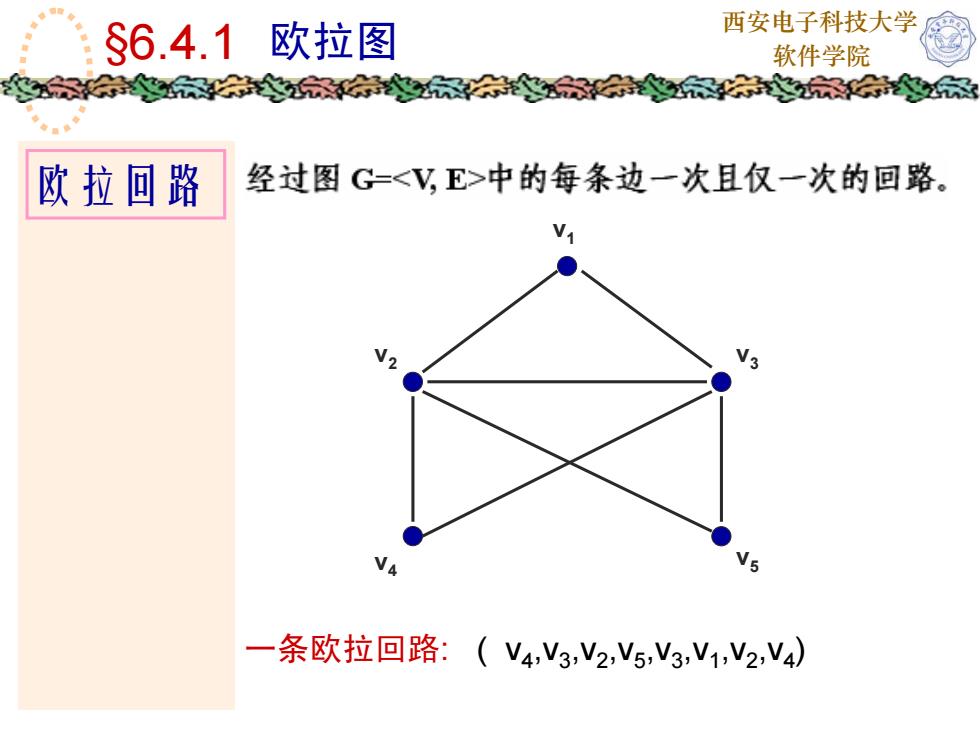
西安电子科技大学 §6.4.1 欧拉图 软件学院 欧拉回路 v1 v2 v3 v4 v5 一条欧拉回路: ( v4 ,v3 ,v2 ,v5 ,v3 ,v1 ,v2 ,v4 )
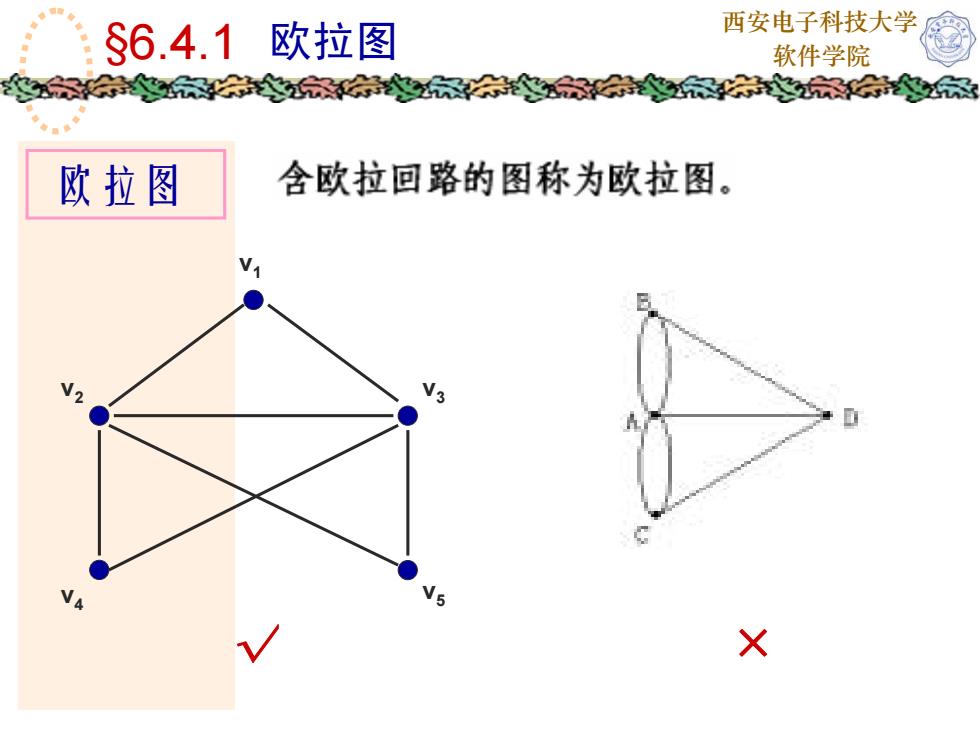
西安电子科技大学欧拉图$6.4.1软件学院含欧拉回路的图称为欧拉图。欧拉图15X
西安电子科技大学 §6.4.1 欧拉图 软件学院 欧拉图 v1 v2 v3 v4 v5 √ ×

西安电子科技大学$6.4.1欧拉图软件学院家【引理】在一个结点度数均为偶数的连通无向图G=中,必存在一条简单回路证明:(构造法)任取结点v1EV,因为v1度数为偶数,o—○所以必存在边与v1关联。取与v1关联的一条边el,令el=(vl,v2)。若v2=v1,则e1是v1结点上的一条自回路,它就是一条简单回路。否则,v2≠v1。因为v2的度数亦为偶数,所以必存在另外一条边e2≠el,并且e2与v2关联,令e2=(v2,v3)。若v3=v2或v3=v1,则找到一条简单回路。否则,v3≠v2且v3v1,因为v3的度数亦为偶数,所以必存在另外一条边e3与v3关联,并且满足e3≠e2且e3≠el。如此下去,由于G中的结点是有限的,因此必存在一条简单回路
西安电子科技大学 §6.4.1 欧拉图 软件学院 【引理】在一个结点度数均为偶数的连通无向图 G=中,必存在一条简单回路。 证明:(构造法) 任取结点v1∈V,因为v1度数为偶数, 所以必存在边与v1关联。 取与v1关联的一条边e1,令e1=(v1 ,v2)。 若v2=v1,则e1是v1结点上的一条自回路,它就是一条简单回 路。否则,v2≠v1。因为v2的度数亦为偶数,所以必存在另外一条 边e2≠e1,并且e2与v2关联,令e2=( v2 ,v3)。 若v3=v2 或v3=v1,则找到一条简单回路。否则,v3≠v2 且 v3≠v1,因为v3的度数亦为偶数,所以必存在另外一条边e3与v3关 联,并且满足e3≠e2且e3≠e1。 . . 如此下去,由于G中的结点是有限的,因此必存在一条简单回路

西安电子科技大学欧拉图$6.4.1 区软件学院家案■定理」无向图G是欧拉图当且仅当G是连通的并且每个结点的度均为偶数。证明:(必要性:G是欧拉图G是连通的且每个结点的度均为偶数)如果G是欧拉图,显然G是连通的。设C为G中的一条欧拉回路,如图所示,当沿着C移动时,通过每个结点将会给该结点带来2度,并需通过关联于这个结点的以前从未走过的两条边
西安电子科技大学 §6.4.1 欧拉图 软件学院 证明:(必要性:G是欧拉图⇒G是连通的且每个 结点的度均为偶数) 如果G是欧拉图,显然G是连通的。设C为G中 的一条欧拉回路,如图所示,当沿着C移动时, 通过每个结点将会给该结点带来2度,并需通过关 联于这个结点的以前从未走过的两条边

西安电子科技大学欧拉图$6.4.1[软件学院(充分性:G是连通的且每个结点的度均为偶数一G是欧拉图)设G连通,并且每个结点的度数均为偶数。根据引理可知:G中必存在简单回路。在图G中的找到一条简单回路E1,若E,中包含G中的所有边,则E,即为一条欧拉回路。否则,从图G中册删掉E,中的所有边,所得子图G'中每个结点的度数仍然为偶数,在G'中必可找到一条简单回路E,如此下去,可以从G中找到一组简单回路E1,E2,,Em且满足:(1)E= E, UE,.---UEm(2)EnE2n---nEm=0
西安电子科技大学 §6.4.1 欧拉图 软件学院 (充分性:G是连通的且每个结点的度均为偶数⇒G是 欧拉图) 设G连通,并且每个结点的度数均为偶数。根据引理可 知:G中必存在简单回路。 在图G中的找到一条简单回路E1,若E1中包含G中的所 有边,则E1即为一条欧拉回路。 否则,从图G中删掉E1中的所有边,所得子图G'中每个 结点的度数仍然为偶数,在G'中必可找到一条简单回路E2 。 . 如此下去,可以从G中找到一组简单回路E1, E2, ., Em 且满足: E= E1 ⋃E2⋃┈⋃Em (1) E1⋂E2⋂┈⋂Em=∅ (2)

西安电子科技大学欧拉图$6.4.1 区软件学院即G中得每一条边在且仅在E,,E,,,E的一个之中。现将简单回路集E,EEm连接成一条简单回路。从E,开始,由于G是连通的,所以在EE中至少有一个,设为E,满足E,与E至少有一个公共结点设为V。(否则由E,导出的子图是一个单独的连通分支,这与G是连通的矛盾。)设E,-(v, Vin, Vi2, Vi3,"", Vim, V), E,= (v, Vj1Vij2 , Vj3,"", Vit, V)则(v,Vi,Vi2,Vi"",VimV,Vj1,Vj2,Vjs"",Vit,V)是一条简单回路,记为E(1)。将E,与E,从简单回路集中删除,将E(1)插入其中。如此下去,直到简单回路集中仅剩下一条回路,即为欧拉回路。故G是欧拉图
西安电子科技大学 §6.4.1 欧拉图 软件学院 即G中得每一条边在且仅在E1,E2,.,Em的一个 之中。 现将简单回路集{E1,E2,.,Em|}连接成一条简单 回路。从E1开始,由于G是连通的,所以在 {E2,.,Em}中至少有一个,设为Ep,满足E1与Ep至 少有一个公共结点设为v。(否则由E1导出的子图 是一个单独的连通分支,这与G是连通的矛盾。) 设E1=(v, v i1, v i2 , v i3,., v im, v),Ep= (v, v j1, v j2 , v j3,., vjt, v) 则(v, v i1, v i2 , v i3,., v im, v, v j1, v j2 , v j3,., vjt, v)是一条简单回路 ,记为E(1) 。 将E1与Ep从简单回路集中删除,将E(1)插入其中。 . 如此下去,直到简单回路集中仅剩下一条回路,即为欧拉回路。 故G是欧拉图

西安电子科技大学$6.4.1欧拉图软件学院教家『推论』无向图G中存在一条欧拉路径,当且仅当G是连通的,并且图中仅有零个或两个奇数度的结点
西安电子科技大学 §6.4.1 欧拉图 软件学院 『推论』无向图G中存在一条欧拉路径,当且仅当G 是连通的,并且图中仅有零个或两个奇数度的结点