
集合与函数根念 吉林省延边二中周国华 一、教材分析 集合语言是现代数学的基本语言,使用集合语言,可以简洁、准确地表达数学的一些 内容。本章中只将集合作为一种语言来学习,学生将学会使用最基本的集合语言去表示有 关的数学对象,发展运用数学语言进行交流的能力. 函数的学习促使学生的数学思维方式发生了重大的转变:思维从静止走向了运动、从 运算转向了关系.函数是高中数学的核心内容,是高中数学课程的一个基本主线,有了这 条主线就可以把数学知识编织在一起,这样可以使我们对知识的掌握更牢固一些。函数与 不等式、数列、导数、立体、解析、算法、概率、选修中的很多专题内容有着密切的联 系。用函数的思想去理解这些内容,是非常重要的出发点,反过来,通过这些内容的学 习,加深了对函数思想的认识.函数的思想方法贯穿于高中数学课程的始终.高中数学课 程中,函数有许多下位知识,如必修1第二章的幂、指、对函数数,在必修四将学习三角 函数。函数是描述客观世界变化规律的重要数学模型. 二、学情分析 1.学生的作业与试卷部分缺失,导致易错问题分析不全面.通过布置易错点分析的任 务,让学生意识到保留资料的重要性 2.学生学基本功较扎实,学习态度较端正,有一定的自主学习能力.但是没有养成及 时复习的习惯,有些内容已经淡忘。通过自主梳理知识,让学生感受复习的必要性,培养 学生良好的复习习惯
集合与函数概念 吉林省延边二中 周国华 一、教材分析 集合语言是现代数学的基本语言,使用集合语言,可以简洁、准确地表达数学的一些 内容.本章中只将集合作为一种语言来学习,学生将学会使用最基本的集合语言去表示有 关的数学对象,发展运用数学语言进行交流的能力. 函数的学习促使学生的数学思维方式发生了重大的转变:思维从静止走向了运动、从 运算转向了关系.函数是高中数学的核心内容, 是高中数学课程的一个基本主线,有了这 条主线就可以把数学知识编织在一起,这样可以使我们对知识的掌握更牢固一些.函数与 不等式、数列、导数、立体、解析、算法、概率、选修中的很多专题内容有着密切的联 系.用函数的思想去理解这些内容,是非常重要的出发点.反过来,通过这些内容的学 习,加深了对函数思想的认识.函数的思想方法贯穿于高中数学课程的始终.高中数学课 程中,函数有许多下位知识,如必修 1 第二章的幂、指、对函数数,在必修四将学习三角 函数.函数是描述客观世界变化规律的重要数学模型. 二、学情分析 1.学生的作业与试卷部分缺失,导致易错问题分析不全面.通过布置易错点分析的任 务,让学生意识到保留资料的重要性. 2.学生学基本功较扎实,学习态度较端正,有一定的自主学习能力.但是没有养成及 时复习的习惯,有些内容已经淡忘.通过自主梳理知识,让学生感受复习的必要性,培养 学生良好的复习习惯.

3.在研究例4时,对分类的情况研究的不全面.为了突破这个难点,应用几何画板制 作了课件,给学生形象、直观的感知,体会二次函数对称轴与所给的区间的位置关系是解 决这类问题的关键 三、设计思略 本节课新课中渗透的理念是:“强调过程教学,启发思维,调动学生学习数学的积极 性”·在本节课的学习过程中,教师没有把梳理好的知识展示给学生,而是让学生自己进 行知识的梳理。一方让学生体会到知识网络化的必要性,另一方面希望学生养成知识梳理 的习惯。在本节课中不断提出问题,采取问题驱动,引导学生积极思考,让学生全面参 与,整个教学过程尊重学生的思维方式,引导学生在“最近发展区”发现问题、解决问 题.通过自主分析、交流合作,从而进行有机建构,解决问题,改变学生模仿式的学习方 式。在教学过程中,渗透了特殊到一般的思想、数形结合思想、函数与方程思想.在教学 过程中通过恰当的应用信息技术,从而突破难点. 四、教学目标分析 (一)知识与技能 1.了解集合的含义与表示,理解集合间的基本关系,集合的基本运算。 A:能从集合间的运算分析出集合的基本关系.B:对于分类讨论问题,能区分取交还是取 并 2.理解函数的定义,掌握函数的基本性质,会运用函数的图象理解和研究函数的性
3.在研究例 4 时,对分类的情况研究的不全面.为了突破这个难点,应用几何画板制 作了课件,给学生形象、直观的感知,体会二次函数对称轴与所给的区间的位置关系是解 决这类问题的关键. 三、设计思路 本节课新课中渗透的理念是:“强调过程教学,启发思维,调动学生学习数学的积极 性”.在本节课的学习过程中,教师没有把梳理好的知识展示给学生,而是让学生自己进 行知识的梳理.一方让学生体会到知识网络化的必要性,另一方面希望学生养成知识梳理 的习惯.在本节课中不断提出问题,采取问题驱动,引导学生积极思考,让学生全面参 与,整个教学过程尊重学生的思维方式,引导学生在“最近发展区”发现问题、解决问 题.通过自主分析、交流合作,从而进行有机建构,解决问题,改变学生模仿式的学习方 式.在教学过程中,渗透了特殊到一般的思想、数形结合思想、函数与方程思想.在教学 过程中通过恰当的应用信息技术,从而突破难点. 四、教学目标分析 (一)知识与技能 1.了解集合的含义与表示,理解集合间的基本关系,集合的基本运算. A:能从集合间的运算分析出集合的基本关系.B:对于分类讨论问题,能区分取交还是取 并. 2.理解函数的定义,掌握函数的基本性质,会运用函数的图象理解和研究函数的性 质.

A:会用定义证明函数的单调性、奇偶性。B:会分析函数的单调性、奇偶性、对称性的关 系 (二)过程与方法 1.通过学生自主知识梳理,了解自己学习的不足,明确知识的来龙去脉,把学习的内 容网络化、系统化. 2.在解决问题的过程中,学生通过自主探究、合作交流,领悟知识的横、纵向联系, 体会集合与函数的本质. (三)情感态度与价值观 在学生自主整理知识结构的过程中,认识到材料整理的必要性,从而形成及时反思的 学习习惯,独立获取数学知识的能力,在解决问题的过程中,学生感受到成功的喜悦,树 立学好数学的信心在例4的解答过程中,渗透动静结合的思想,让学生养成理性思维的 品质。 五、重难点分析 重点:掌握知识之间的联系,洞悉问题的考察点,能选择合适的知识与方法解决问 难点:含参问题的讨论,函数性质之间的关系
A:会用定义证明函数的单调性、奇偶性.B:会分析函数的单调性、奇偶性、对称性的关 系. (二)过程与方法 1.通过学生自主知识梳理,了解自己学习的不足,明确知识的来龙去脉,把学习的内 容网络化、系统化. 2.在解决问题的过程中,学生通过自主探究、合作交流,领悟知识的横、纵向联系, 体会集合与函数的本质. (三)情感态度与价值观 在学生自主整理知识结构的过程中,认识到材料整理的必要性,从而形成及时反思的 学习习惯,独立获取数学知识的能力.在解决问题的过程中,学生感受到成功的喜悦,树 立学好数学的信心.在例 4 的解答过程中,渗透动静结合的思想,让学生养成理性思维的 品质. 五、重难点分析 重点:掌握知识之间的联系,洞悉问题的考察点,能选择合适的知识与方法解决问 题. 难点:含参问题的讨论,函数性质之间的关系.

六.知识梳理(约10分钟) 提出问思 问题1:把本章的知识结构用框图形式表示出来。 问题2:一个集合中的元素应当是确定的、互异的、无序的,你能结合具体实例说明 集合的这些基本要求吗? 问题3:类比两个数的关系,思考两个集合之间的基本关系。类比两个数的运算,思 考两个集合之间的基本运算,交、并、补. 问题4:通过本章学习,你对函数概念有什么新的认识和体会吗? 请结合具体实例分析,表示函数的三种方法,每一种方法的特点. 问题5:分析研究函数的方向,它们之间的联系 在前一次晚自习上,学生相互展示自己的结果,通过相互讨论,每组提供最佳的方 案.在自己的原有方案的基础上进行补充与完善. 学生回答问题要点预设如下: 1.集合语言可以简洁准确表达数学内容
六.知识梳理(约 10 分钟) 提出问题 问题 1:把本章的知识结构用框图形式表示出来. 问题 2:一个集合中的元素应当是确定的、互异的、无序的,你能结合具体实例说明 集合的这些基本要求吗? 问题 3:类比两个数的关系,思考两个集合之间的基本关系.类比两个数的运算,思 考两个集合之间的基本运算,交、并、补. 问题 4:通过本章学习,你对函数概念有什么新的认识和体会吗? 请结合具体实例分析,表示函数的三种方法,每一种方法的特点. 问题 5:分析研究函数的方向,它们之间的联系. 在前一次晚自习上,学生相互展示自己的结果,通过相互讨论,每组提供最佳的方 案.在自己的原有方案的基础上进行补充与完善. 学生回答问题要点预设如下: 1.集合语言可以简洁准确表达数学内容.

2.运用集合与对应进一步描述了函数的概念,与初中的函数的定义比较,突出了函数 的本质函数是描述变量之间依赖关系的重要数学模型。 3.函数的表示方法主要有三种,这三种表示方法有各自的适用范围,要根据具体情况 选用 4.研究函数的性质时,一般先从几何直观观察图象入手,然后运用自然语言描述函数 的图象特征,最后抽象到用数学符号刻画相应的数量特征,也是数学学习和研究中经常使 用的方法 设计意图:通过布置任务,让学生充分的认识自己在学习的过程中,哪些知识学习的 不透彻.让学生更有针对的进行复习,让复习进行的更有效。让学生体会到知识的横向联 系与纵向联系。通过类比初中与高中两种函数的定义,让学生体会到两种函数的定义本质 是一样的 七、易错点分析(约3分钟) 问恩6:集合中的易错问题,函数中的易错问题?主要是作业、训练、考试中出现的问 题? (任务提前布置,由课代表汇总,并且在教学课件中体现。教师不进行修改,呈现的是原始 的) 数师展示学和成果并进行点评
2.运用集合与对应进一步描述了函数的概念,与初中的函数的定义比较,突出了函数 的本质函数是描述变量之间依赖关系的重要数学模型. 3.函数的表示方法主要有三种,这三种表示方法有各自的适用范围,要根据具体情况 选用. 4.研究函数的性质时,一般先从几何直观观察图象入手,然后运用自然语言描述函数 的图象特征,最后抽象到用数学符号刻画相应的数量特征,也是数学学习和研究中经常使 用的方法. 设计意图:通过布置任务,让学生充分的认识自己在学习的过程中,哪些知识学习的 不透彻.让学生更有针对的进行复习,让复习进行的更有效.让学生体会到知识的横向联 系与纵向联系.通过类比初中与高中两种函数的定义,让学生体会到两种函数的定义本质 是一样的. 七、易错点分析(约 3 分钟) 问题 6:集合中的易错问题,函数中的易错问题?主要是作业、训练、考试中出现的问 题? (任务提前布置,由课代表汇总,并且在教学课件中体现.教师不进行修改,呈现的是原始 的) 教师展示学和成果并进行点评.
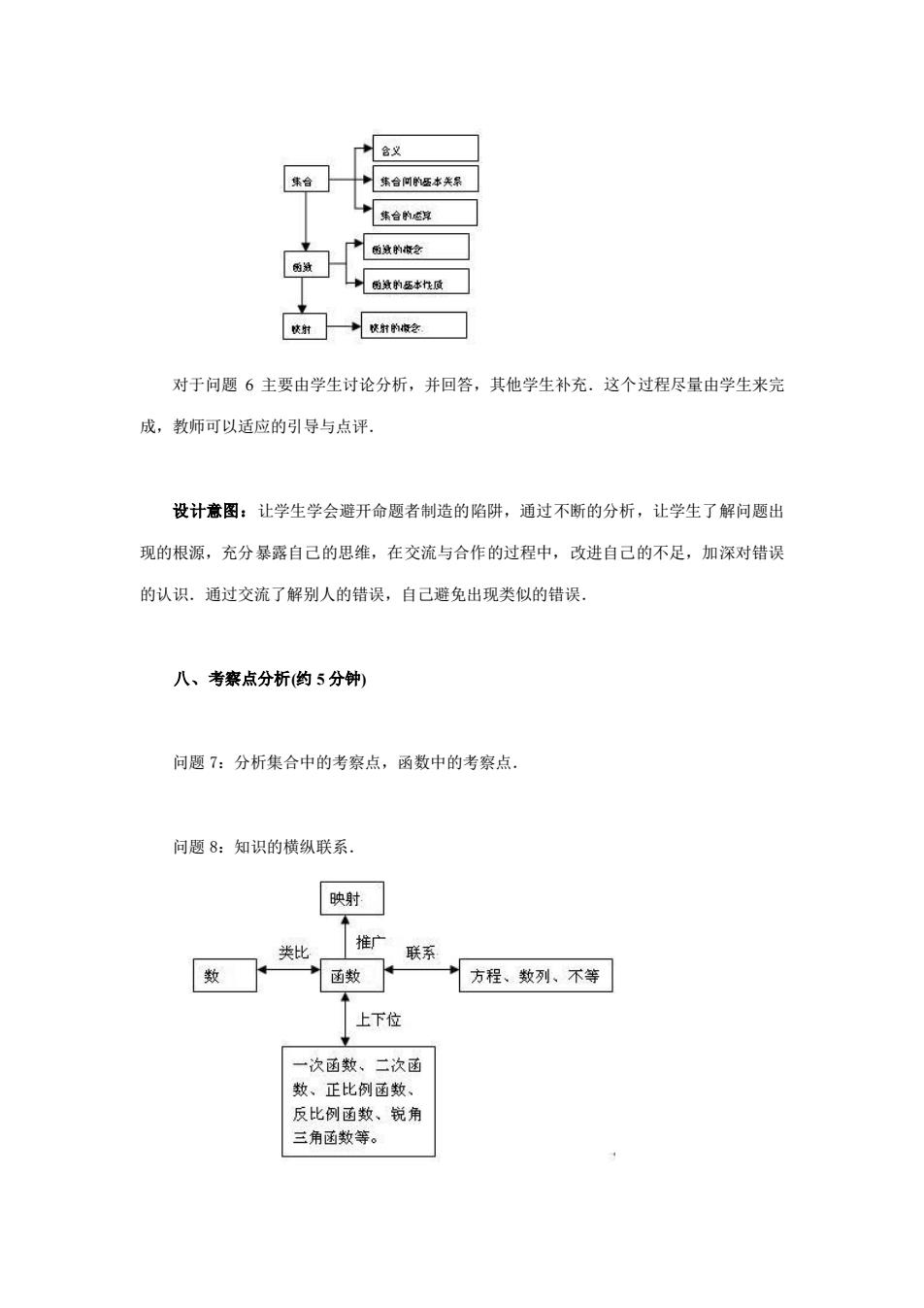
对于问题6主要由学生讨论分析,并回答,其他学生补充。这个过程尽量由学生来完 成,教师可以适应的引导与点评。 设计意图:让学生学会避开命题者制造的陷阱,通过不断的分析,让学生了解问题出 现的根源,充分暴露自己的思维,在交流与合作的过程中,改进自己的不足,加深对错误 的认识。通过交流了解别人的错误,自己避免出现类似的错误 八、考泰点分析(的5分钟) 问题7:分析集合中的考察点,函数中的考察点。 问愿8:知识的横纵联系, 映射 推广 数☐ 类比 联系 西数 方程、效列、不等 上下位 一次函数、二次函 数、正比例函数、 反比例西数、锐角 三角西数等
对于问题 6 主要由学生讨论分析,并回答,其他学生补充.这个过程尽量由学生来完 成,教师可以适应的引导与点评. 设计意图:让学生学会避开命题者制造的陷阱,通过不断的分析,让学生了解问题出 现的根源,充分暴露自己的思维,在交流与合作的过程中,改进自己的不足,加深对错误 的认识.通过交流了解别人的错误,自己避免出现类似的错误. 八、考察点分析(约 5 分钟) 问题 7:分析集合中的考察点,函数中的考察点. 问题 8:知识的横纵联系.

学生回答问题要点预设如下: 1.集合中元素的互异性 2.A二B,则集合A可以是空集」 3.交集与并集的区分,即何时取交,何时取并,特别是含参的分类讨论问题 4.函数的单调性与奇偶性的证明】 5.作业与试卷中出现的问题。 6.学生分析本章的考察点,主要分析考察的知识点、思想方法等方面。 设计意图:让学生了解考察点,才能知道命题者的考察意图,才能选择合适的知识与 思想方法来解答。例如如果试题中出现集合,无论试题以什么形式出现,考察点基本是集 合间的基本关系、集合的运算。 九、典型问题分析 例1:设集合A=(x2+4x=0) B={x天+2a+)x+d2-1=0)(1)若BGA,求实数a的值 (2)若A门B=B,求a的值:
学生回答问题要点预设如下: 1.集合中元素的互异性. 2. ,则集合 A 可以是空集. 3.交集与并集的区分,即何时取交,何时取并,特别是含参的分类讨论问题. 4.函数的单调性与奇偶性的证明. 5.作业与试卷中出现的问题. 6.学生分析本章的考察点,主要分析考察的知识点、思想方法等方面. 设计意图: 让学生了解考察点,才能知道命题者的考察意图,才能选择合适的知识与 思想方法来解答.例如如果试题中出现集合, 无论试题以什么形式出现,考察点基本是集 合间的基本关系、集合的运算. 九、典型问题分析 例 1:设集合 (1)若 ,求实数 的值; (2)若 ,求 的值;

(3)若AUB=B,求a的值,教师点评,同时板书, ()答案:a≤-1或a=1y (2)答案:a=1或a≤1 (3)答案:a=1. 由学生分析问题的考察点,包括知识与数学思想.(预设有以下几个方面)从知识点 来分析,这是集合问题。考察点主要为集合的表示方法、集合中元素的特性、集合间的基 本关系、集合的运算等。学生在解第1个问时,可能漏掉特殊情况。第2、3问可能会遇到 一定的障碍,可以给学生时间进行充分的思考. 设计意图:让学生体会到分析考察点的好处,养成解愿之前分析考察点的习惯。能顺 利的找到问题的突破口,为后续的解答扫清障碍.通过一题多问、一愿多解、多题归一, 让学生主动的形成发散思维,主动应用转化与化归的思想 例2:已知函数(闭是定义在R上的奇函数,当x20时, x)=x1+x),求函数的解析式. 变式:函数是偶函数 教师对生回答进行点评。并板书
(3)若 ,求 的值.教师点评,同时板书. (1)答案: 或 ; (2)答案: 或 ; (3)答案: . 由学生分析问题的考察点,包括知识与数学思想.(预设有以下几个方面)从知识点 来分析,这是集合问题.考察点主要为集合的表示方法、集合中元素的特性、集合间的基 本关系、集合的运算等.学生在解第 1 个问时,可能漏掉特殊情况.第 2、3 问可能会遇到 一定的障碍,可以给学生时间进行充分的思考. 设计意图:让学生体会到分析考察点的好处,养成解题之前分析考察点的习惯.能顺 利的找到问题的突破口,为后续的解答扫清障碍.通过一题多问、一题多解、多题归一, 让学生主动的形成发散思维,主动应用转化与化归的思想. 例 2:已知函数 是定义在 R 上的奇函数,当 时, ,求函数的解析式. 变式:函数是偶函数 教师对生回答进行点评.并板书.

∫x(1+x,x20 f闭=0-.x0,所以可以研究一x的函数值。 设计意图:学生在思考的过程中,体会数形结合思想。函数的奇偶性与函数的图象的 关系,可以根据奇偶性绘制函数图象,也可以通过函数的图象分析函数的奇偶性,两者是 相辅相承的。体会转化与化归的思想,把要研究的转化为已知的。考察函数的单调性的证
学生分析考察点、解题思路,如果不完善,其他学生补充. 学生回答问题要点预设如下: 1.考察点为函数的奇偶性与函数图象的关系. 2.函数的奇偶性的定义. 3.转化与化归的思想. 法一:本题即求 ,函数的解析式,可先利用函数的奇偶性绘制函数的图象,把本题 转化为二次函数的图象与解析式的问题. 法二:本法更具有一般性,已知 时,函数的解析式,要分析 时的函数对应关系,即当一个数小于零时,函数值 应当怎样计算.由于函数具有奇偶性,即一个数与它的相反数的函数值之间有关系, ,所以可以研究 的函数值. 设计意图:学生在思考的过程中,体会数形结合思想.函数的奇偶性与函数的图象的 关系,可以根据奇偶性绘制函数图象,也可以通过函数的图象分析函数的奇偶性,两者是 相辅相承的.体会转化与化归的思想,把要研究的转化为已知的.考察函数的单调性的证

明,函数的奇偶性与单调性之间的关系,体会知识的纵向联系。体会转化与化归的思想、 特殊与一般的数学思想,让学生体会到问题后面隐含的本质, 例3:已知了()是偶函数,而且在(0,+0)上是减函数,判断/()在-0,0)上是增函数 还是减函数,并证明你的判断。 变式1:函数为奇函数 变式2:你能分析奇函数(偶函数)在对称区间上的单调性的关系吗?试从数形两个方面来分 析. 学生分析考察点、解题思路,如果不完善,其他学生补充。 学生回答问题要点预设如下: 1,考察点为函数的奇偶性与单调性的关系 2.函数的单调性的定义 3.数形结合、转化与化归的思想。 法一:通过函数的图象分析 法二:把要研究的范围转化为己知的范围
明,函数的奇偶性与单调性之间的关系,体会知识的纵向联系.体会转化与化归的思想、 特殊与一般的数学思想,让学生体会到问题后面隐含的本质. 例 3:已知 是偶函数,而且在 上是减函数,判断 在 上是增函数 还是减函数,并证明你的判断. 变式 1:函数为奇函数 变式 2:你能分析奇函数(偶函数)在对称区间上的单调性的关系吗?试从数形两个方面来分 析. 学生分析考察点、解题思路,如果不完善,其他学生补充. 学生回答问题要点预设如下: 1.考察点为函数的奇偶性与单调性的关系. 2.函数的单调性的定义. 3.数形结合、转化与化归的思想. 法一:通过函数的图象分析. 法二:把要研究的范围转化为已知的范围.