西安电子科技大学离散数学软件学院第四篇图论第6章图论第28课时6.1图的基本概念(2)一→第29课时6.2路径与回路→第30课时6.3图的矩阵表示第31-32课时6.4欧拉图与汉密尔顿图6.5平面图第33-34课时一第35课时6.6图的着色6.7 树第36-37课时E6.8图的应用第38课时
西安电子科技大学 离散数学 软件学院 第四篇 图论 6.1 图的基本概念(2) 第6章 图论 6.4 欧拉图与汉密尔顿图 6.2 路径与回路 6.5 平面图 第29课时 第33-34课时 第30课时 6.3 图的矩阵表示 第35课时 6.6 图的着色 第31-32课时 第36-37课时 6.7 树 第28课时 第38课时 6.8 图的应用

西安电子科技大学$6.1.4特殊的图软件学院零图由若干个孤立结点组成的图称为零图。平凡图仅含单个孤立结点的图称为平凡图
西安电子科技大学 特殊的图 软件学院 零图 §6.1.4 平凡图

西安电子科技大学$6.1.4特殊的图软件学院(1)有向完全图完全图有向图G=中,若E=V×V,则称G为有向完全图。图9.1-4所示是四个结点的有向完全图四个结点的有向完全图
西安电子科技大学 软件学院 完全图 §6.1.4 特殊的图
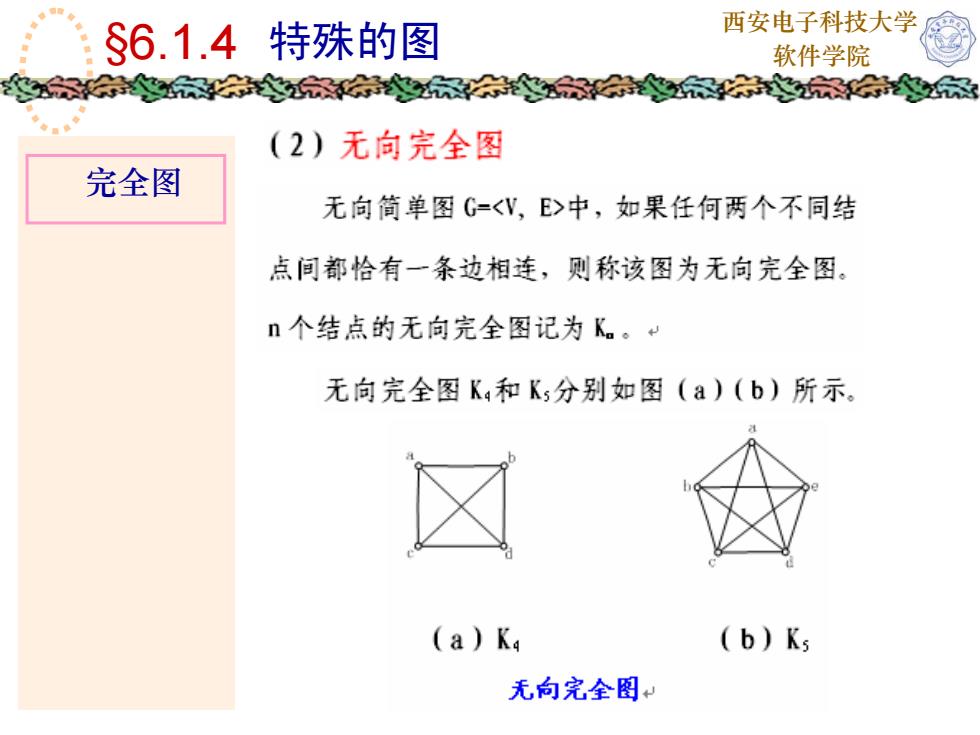
西安电子科技大学$6.1.4特殊的图软件学院教家家家(2)无向完全图完全图无向简单图G-中,如果任何两个不同结点间都恰有一条边相连,则称该图为无向完全图。n个结点的无向完全图记为K。。+无向完全图K.和Ks分别如图(a)(b)所示。X(a) K.(b) Ks无向完全图
西安电子科技大学 特殊的图 软件学院 完全图 §6.1.4
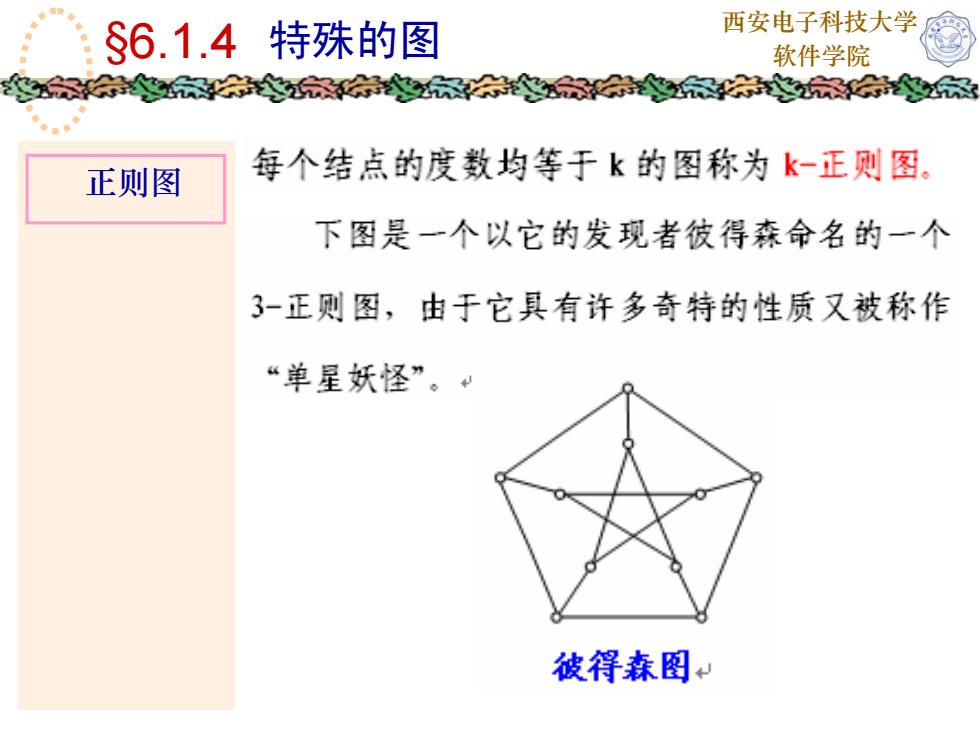
西安电子科技大学$6.1.4特殊的图软件学院家每个结点的度数均等于k的图称为k-正则图正则图下图是一个以它的发现者彼得森命名的一个3-正则图,由于它具有许多奇特的性质又被称作“单星妖怪”。彼得森图
西安电子科技大学 特殊的图 软件学院 正则图 §6.1.4

西安电子科技大学特殊的图$6.1.4软件学院无向图G-中的结点集合V如果可以划分二部图成两个不相交的子集X和Y,使得G中的每一条边的一个端点在X中而另一个端点在Y中,则称G为二部图,记为G-
西安电子科技大学 特殊的图 软件学院 二部图 §6.1.4
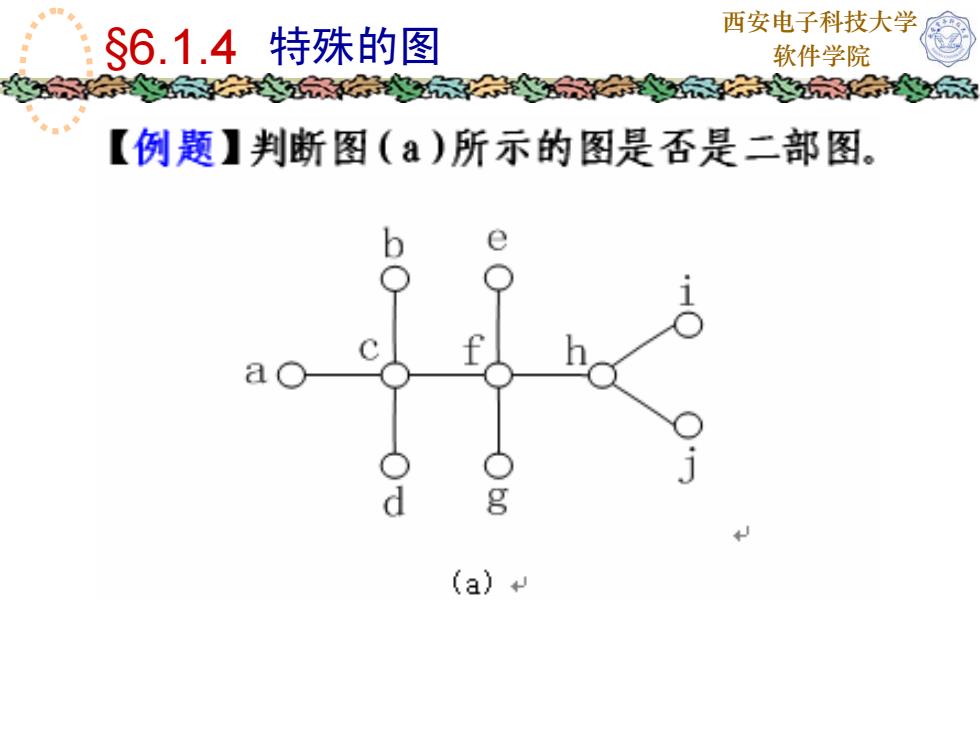
西安电子科技大学$6.1.4特殊的图软件学院【例题】判断图(a)所示的图是否是二部图。ebOOtaO1Ogd(a)
西安电子科技大学 §6.1.4 特殊的图 软件学院

西安电子科技大学$6.1.4特殊的图软件学院bACBA
西安电子科技大学 §6.1.4 特殊的图 软件学院
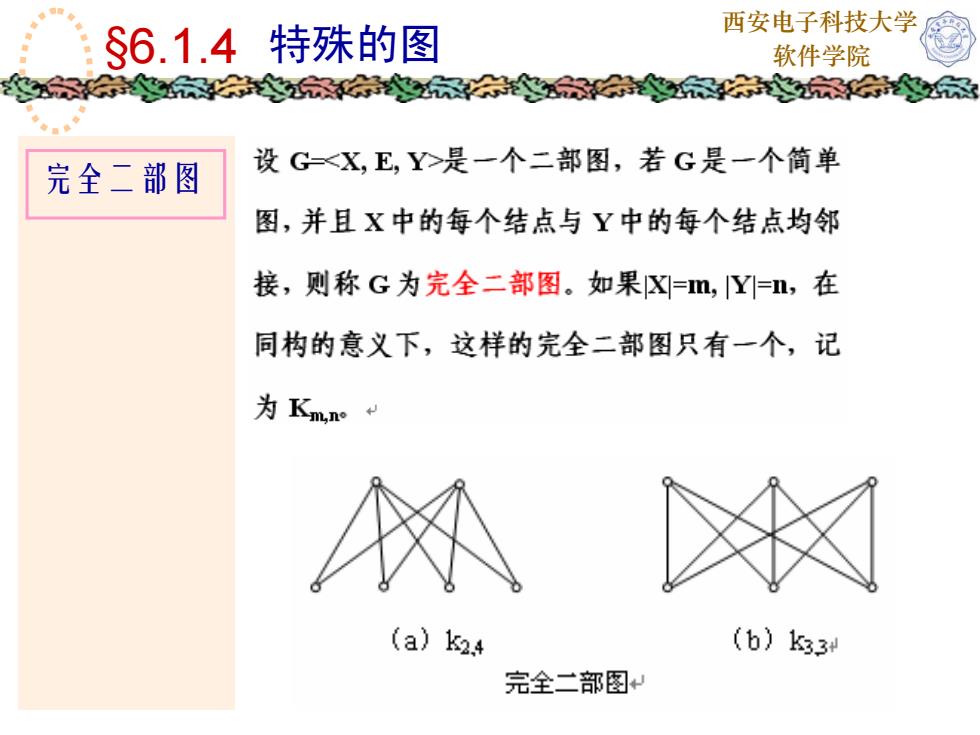
西安电子科技大学$6.1.4特殊的图软件学院家设G-是一个二部图,若G是一个简单完全二部图图,并且X中的每个结点与Y中的每个结点均邻接,则称G为完全二部图。如果X=m,YI=n,在同构的意义下,这样的完全二部图只有一个,记为 Km,n。(a) k24(b) k33t完全二部图+
西安电子科技大学 特殊的图 软件学院 完全二部图 §6.1.4

西安电子科技大学$6.1.5图的操作和运算软件学院家设图Gr=,G2=。定义G与G2的若干运算如下:(1)并Gi UG2=(2)交GinG2=(3)差G1-G2=其中V3=(Vi-V2)UEi-E,中边所关联的结点)(4)环和G1田G2=(GiUG2)-(G1NG2)
西安电子科技大学 §6.1.5 图的操作和运算 软件学院