
西安电子科技大学离散数学软件学院第二篇集合论第3章集合与关系第13课时V3.1集合及其运算第14课时3.2二元关系→第15课时3.3集合上的二元关系及其特性第16课时3.4关系的闭包运算3.5等价关系第17-18课时第19-20课时3.6序关系
西安电子科技大学 离散数学 软件学院 第二篇 集合论 第13课时 3.1 集合及其运算 第3章 集合与关系 3.4 关系的闭包运算 3.2 二元关系 3.5 等价关系 第14课时 第16课时 第17-18课时 第15课时 3.3 集合上的二元关系及其特性 第19-20课时 3.6 序关系

西安电子科技大学$3.2.1两个集合的笛卡儿积软件学院茶家家两个元素a和b组成的具有固定次序的序列,序偶记为。例如:表示某火车行驶的起点和终点。《≠两个序偶=的充要条件是:ai=a2且bi=b2
西安电子科技大学 两个集合的笛卡儿积 软件学院 序偶 §3.2.1 两个元素a和b组成的具有固定次序的序列, 记为 。 两个序偶=的充要条件是: a 1 =a 2 且b 1 =b 2 例如: 表示某火车行驶的起点和终点。 ≠

西安电子科技大学$3.2.1两个集合的笛卡儿积软件学院家笛卡儿积设A和B是两个集合,称集合AxB={aEA^bEB为集合A和B的笛卡儿积或叉集
西安电子科技大学 软件学院 笛卡儿积 §3.2.1 两个集合的笛卡儿积 设A和B是两个集合,称集合 为集合A和B的笛卡儿积或叉集。 × = |,{ ∈ ∧ ∈ BbAabaBA }

西安电子科技大学S3.2.1两个集合的笛卡儿积软件学院茶家【例题】设A=a,b),B={a,β),求AXB解答:AxB={,,,}
西安电子科技大学 软件学院 【例题】设A={a, b}, B={α, β},求A×B §3.2.1 两个集合的笛卡儿积 解答: A×B={,,,}
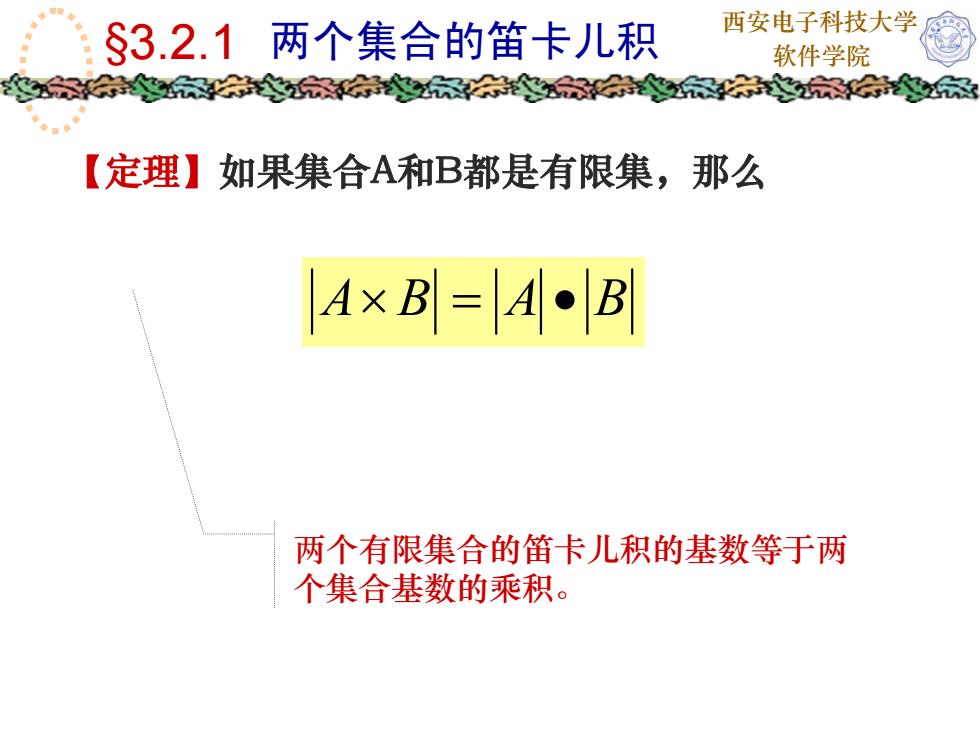
西安电子科技大学$3.2.1两个集合的笛卡儿积软件学院家家【定理】如果集合A和B都是有限集,那么A×B=|A·|Bl两个有限集合的笛卡儿积的基数等于两个集合基数的乘积
西安电子科技大学 §3.2.1 两个集合的笛卡儿积 软件学院 【定理】如果集合A和B都是有限集,那么 •=× BABA 两个有限集合的笛卡儿积的基数等于两 个集合基数的乘积

西安电子科技大学S3.2.2 二元关系的定义软件学院两个集合A和B的笛卡儿积AXB的子集二元关系称为A到B的二元关系。设R二A×B,若ER,则称x与y有R关系,记为:xRy若ER,则称x与y没有R关系,记为:xRy
西安电子科技大学 §3.2.2 二元关系的定义 软件学院 二元关系 两个集合A和B的笛卡儿积A×B的子集, 称为A到B的二元关系。 设R⊆A×B,若∈R,则称x与y有 R关系,记为: xRy 若∈R,则称x与y没有R关系,记为: / yRx
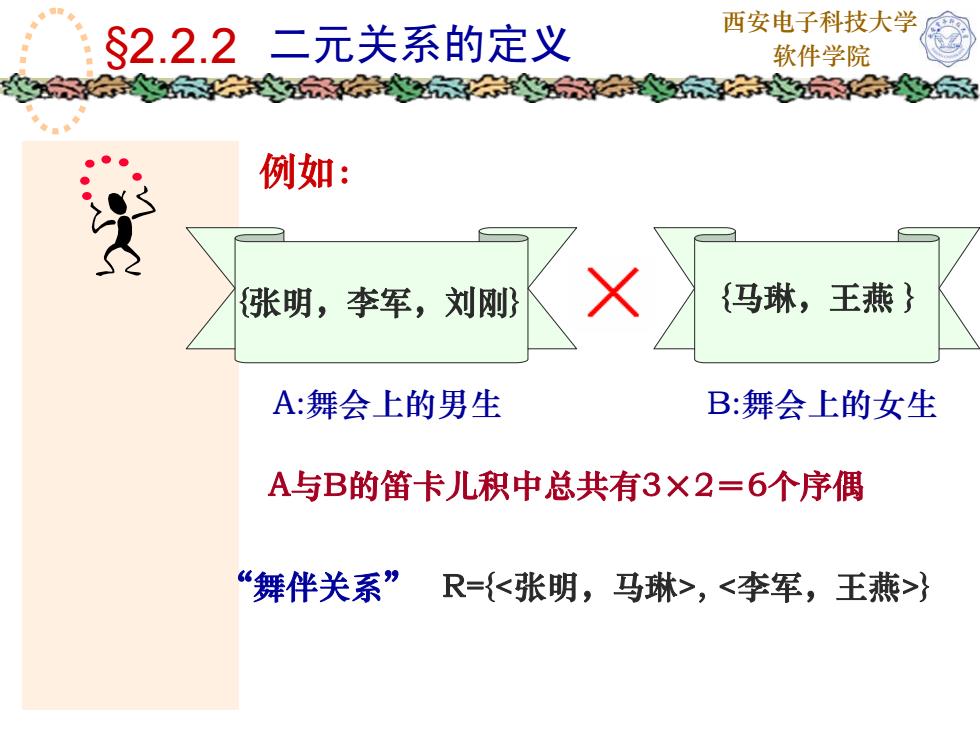
西安电子科技大学2二元关系的定义$2.2.2软件学院乐例如:X{冯琳,王燕}(张明,李军,刘刚)A:舞会上的男生B:舞会上的女生A与B的笛卡儿积中总共有3×2=6个序偶“舞伴关系”R={,}
西安电子科技大学 软件学院 “舞伴关系” R={, } {张明,李军,刘刚} A:舞会上的男生 {马琳,王燕 } B:舞会上的女生 A与B的笛卡儿积中总共有3×2=6个序偶 §2.2.2 二元关系的定义 例如:

西安电子科技大学S3.2.2二元关系的定义软件学院茶教家家家设R是集合A到集合B的二元关系。集合A称为R的前域。前域陪域集合B称为R的陪域。domR = (x /(Ey)(E R))定义域值域ranR = (y|(Fx)(E R))
西安电子科技大学 §3.2.2 二元关系的定义 软件学院 前域 集合A称为R的前域。 设R是集合A到集合B的二元关系。 陪域 定义域 值域 集合B称为R的陪域。 = ∃ >∈∈< RyxxyranR )},)((|{
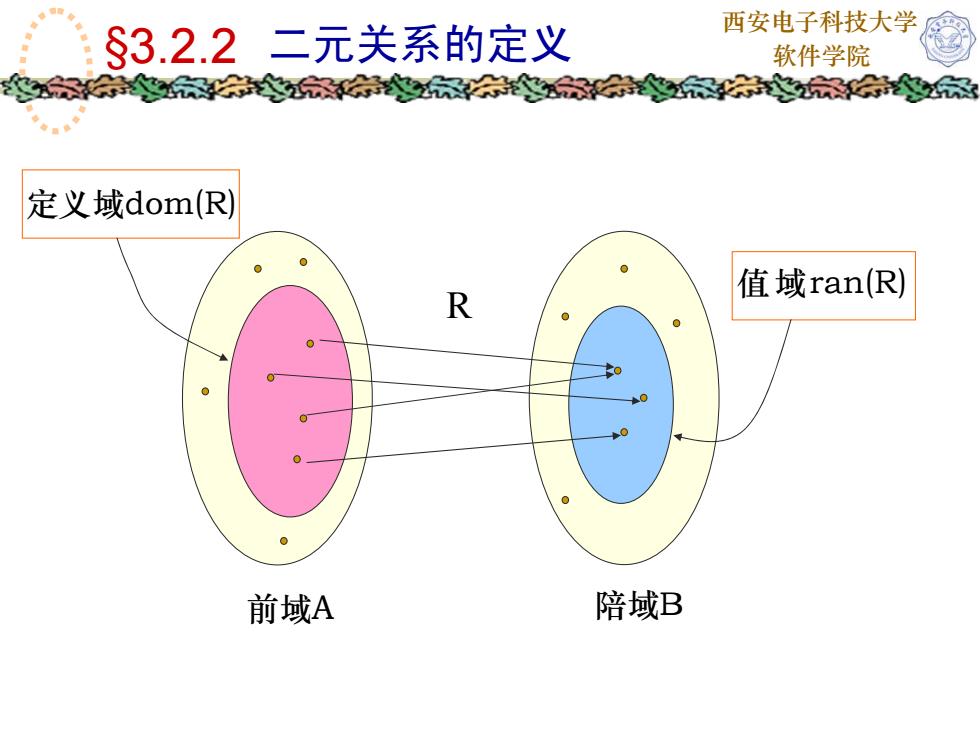
西安电子科技大学$3.2.2二元关系的定义软件学院茶定义域dom(R值域ran(R)R陪域B前域A
西安电子科技大学 软件学院 值域ran(R) 定义域dom(R) 前域A 陪域B R §3.2.2 二元关系的定义

西安电子科技大学S3.2.2二元关系的定义软件学院家教家思考题设集合A和B都是有限集合,1A|=m,IB|=n。请问A到B上可以定义多少个不同的二元关系?解答:A与B的笛卡儿积有多少个不同的子集,在A到B上就可以定义多少个不同的二元关系,因此:p(A× B)= 2mn
西安电子科技大学 §3.2.2 二元关系的定义 软件学院 【思考题】设集合A和B都是有限集合,|A|=m, |B|=n。请问A到B上可以定义多少个不同的二 元关系? nm BA ⋅ ρ =× 2)( 解答:A与B的笛卡儿积有多少个不同的子集,在A到B 上就可以定义多少个不同的二元关系,因此: