
西安电子科技大学离散数学软件学院第一篇数理逻辑第1章命题逻辑1.1命题第1课时7第2课时1.2命题公式→第3课时1.3逻辑等价式与永真蕴含式第4课时之1.4主范式第5课时1.5命题逻辑的推理与证明方法一第6课时之1.6命题逻辑的应用
西安电子科技大学 离散数学 软件学院 第一篇 数理逻辑 第1课时 1.1 命题 第1章 命题逻辑 1.3 逻辑等价式与永真蕴含式 1.2 命题公式 1.4 主范式 1.5 命题逻辑的推理与证明方法 第2课时 第3课时 第4课时 第5课时 第6课时 1.6 命题逻辑的应用
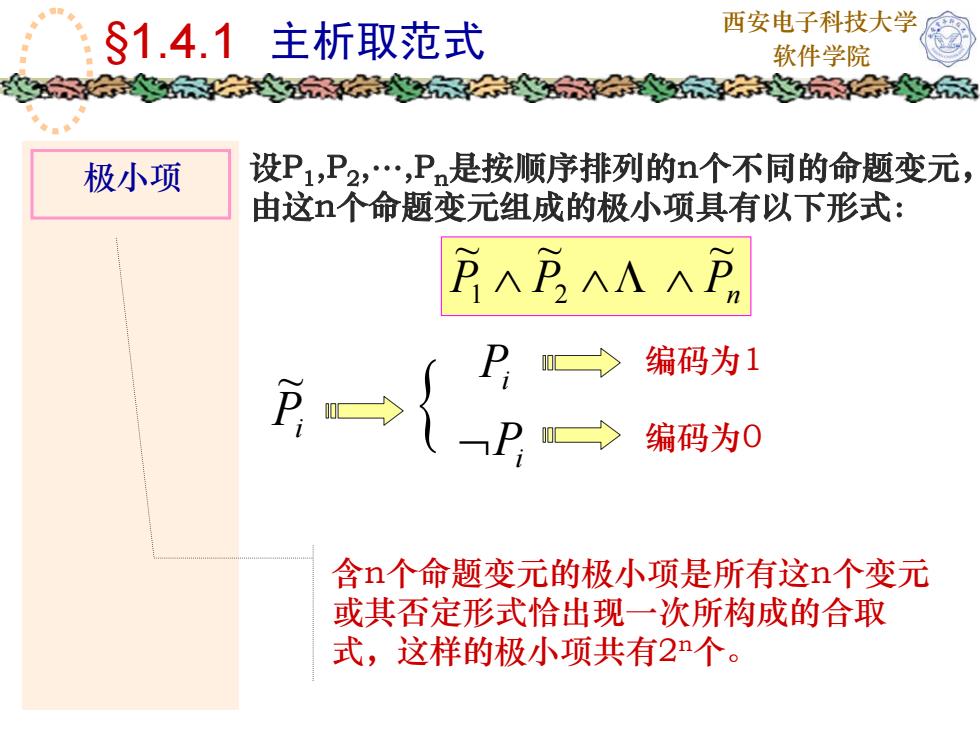
西安电子科技大学$1.4.13主析取范式软件学院家设P1,P2,,Pn是按顺序排列的n个不同的命题变元极小项由这n个命题变元组成的极小项具有以下形式:PPAAP编码为1编码为0含n个命题变元的极小项是所有这n个变元或其否定形式恰出现一次所构成的合取式,这样的极小项共有2n个
西安电子科技大学 §1.4.1 主析取范式 软件学院 极小项 含n个命题变元的极小项是所有这n个变元 或其否定形式恰出现一次所构成的合取 式,这样的极小项共有2n个。 设P1 ,P2 ,.,Pn 是按顺序排列的n个不同的命题变元, 由这n个命题变元组成的极小项具有以下形式: PPP n ~ ~ ~ ∧ Λ 21 ∧∧ Pi ~ { Pi ¬Pi 编码为1 编码为0
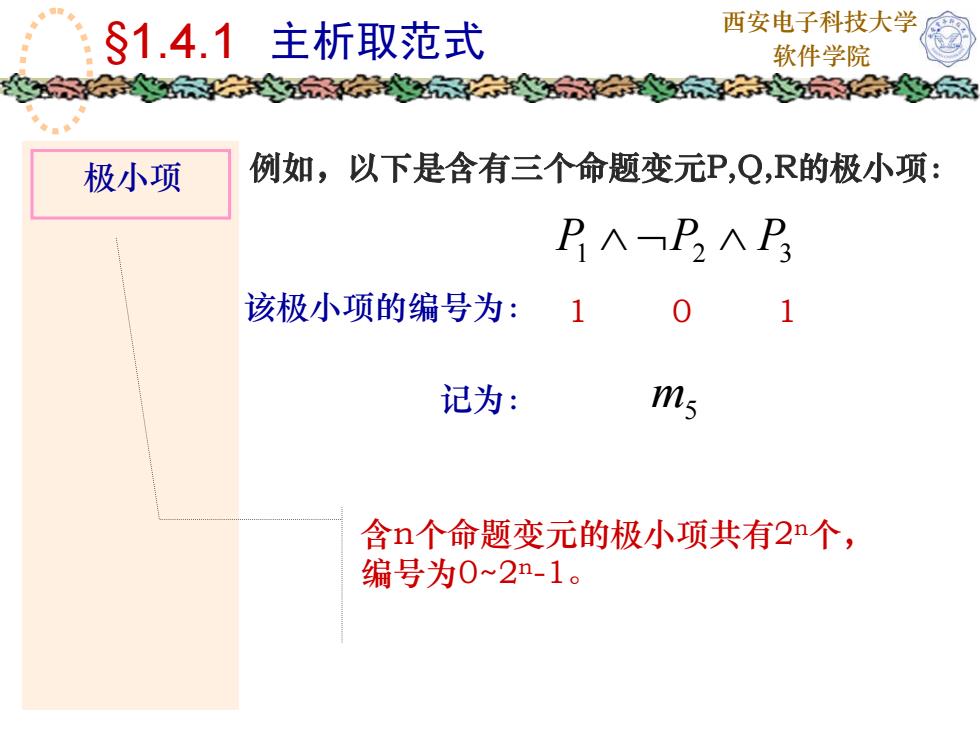
西安电子科技大学$1.4.1主析取范式软件学院家例如,以下是含有三个命题变元P,Q,R的极小项:极小项P-PP该极小项的编号为:011ms记为:含n个命题变元的极小项共有2n个,编号为0~2n-1
西安电子科技大学 §1.4.1 主析取范式 软件学院 极小项 含n个命题变元的极小项共有2n个, 编号为0~2n-1。 例如,以下是含有三个命题变元P,Q,R的极小项: ∧ ¬ ∧ PPP 321 该极小项的编号为: 1 0 1 记为: m5

西安电子科技大学S1.4.1主析取范式软件学院教家家【例题】写出含有三个命题变元P,Q,R的所有的极小项。000mo=-PA-QA-R001-PA-QARmi=PAQA-R010m2"PAQAR011m3100PA-QA-Rm4=101PA-QARms110PAQA-Rm6111mz=PAQAR
西安电子科技大学 软件学院 【例题】写出含有三个命题变元P,Q,R的所有的极小项。 000 m0 = ¬ ∧ ¬ ∧ ¬RQP 001 m1 = ¬ ∧ ¬ ∧ RQP ¬ ∧ ∧ ¬RQP ¬ ∧ ∧ RQP ∧ ¬ ∧ ¬RQP ∧ ¬ ∧ RQP ∧ ∧ ¬RQP ∧ ∧ RQP 010 m2 = 011 m3 = 100 m4 = 101 m5 = 110 m6 = 111 m7 = §1.4.1 主析取范式

西安电子科技大学$1.4.13主析取范式软件学院家家极小项具有以下性质:(1)每个极小项当其赋值指派与其编号相同时其真值为T,并在其余2n-1种赋值指派下其真值均为F;(2)任意两个不同的极小项的合取式永假;itjm,^m,←F(3)所有极小项的析取式永真。n_V.m,=moVm,VAVm"--T
西安电子科技大学 §1.4.1 主析取范式 软件学院 极小项具有以下性质: (1)每个极小项当其赋值指派与其编号相同时其真 值为T,并在其余2 n-1种赋值指派下其真值均为F; (2)任意两个不同的极小项的合取式永假; ∧ ji ⇔ Fmm i ≠ j (3)所有极小项的析取式永真。 n Tmmmm n i i ⇔∨∨∨=∨ − − = 10 12 12 0 Λ

西安电子科技大学$1.4.1 主析取范式软件学院若干个极小项的析取式,如果它与命题公式主析取范式A等价,那么称该式为A的主析取范式。i e(0,1,A,2" -1)A←m,m,AVmi(0≤k≤2")当k=0时AFA是矛盾式AGTA是重言式当k=2n时
西安电子科技大学 §1.4.1 主析取范式 软件学院 主析取范式 若干个极小项的析取式,如果它与命题公式 A等价,那么称该式为A的主析取范式。 k ∨ Λ mm ii ∨∨ mi A ⇔ 1 2 ( ) n k ≤≤ 20 当k=0时 ⇔ FA A是矛盾式 ∈ − }12,1,0{ n ki Λ 当k=2n时 ⇔ TA A是重言式

西安电子科技大学$1.4.1 主析取范式软件学院【例题】求命题公式A=-P(Q→R)的主析取范式。方法一、真值表法Q→R-PA(Q-→R)H-1001110010001PA(Q-R)≤(-PA-QA-R)M-PA-QAR)Y(-PAQAR) 2(0, 1, 3)
西安电子科技大学 软件学院 【例题】求命题公式A=¬P ∧ (Q → R)的主析取范式。 方法一、真值表法 §1.4.1 主析取范式

西安电子科技大学主析取范式$1.4.1软件学院【例题】求命题公式A=-P^(Q→R)的主析取范式。方法二、等价推演法A介-PA(Q VR)(-P^-Q)V(-P^R)↑(-P-Q A(RV-R))V(-PA(OV-Q)^ R)介(-PA-OAR)V-PA-OA-R)V(-PAQ AR) V (-PA-QA R)-PA(Q—R)(-PA-QA-R) V-PA-QAR) Y(-PAQAR) Z(0, 1, 3)
西安电子科技大学 软件学院 【例题】求命题公式A=¬P∧(Q→R)的主析取范式。 方法二、等价推演法 A ⇔ ¬P∧(¬ Q ∨R) ⇔ (¬P∧¬ Q )∨(¬P∧R) ⇔ (¬P∧¬ Q ∧(R∨¬R) )∨(¬P∧(Q∨¬ Q)∧ R) ⇔ (¬P∧¬ Q ∧R)∨ (¬P∧¬ Q∧¬R ) ∨ (¬P∧Q ∧R) ∨ (¬P∧¬ Q∧ R) §1.4.1 主析取范式
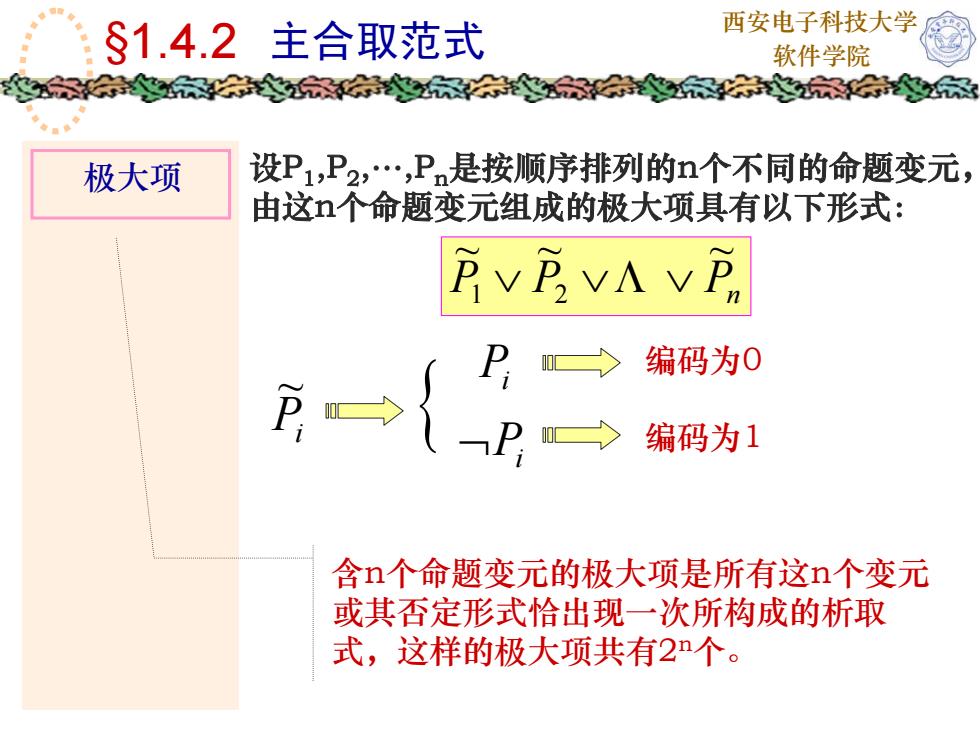
西安电子科技大学$1.4.2主合取范式软件学院家设P1,P2,Pn是按顺序排列的n个不同的命题变元极大项由这n个命题变元组成的极大项具有以下形式:PVPVAVP编码为0编码为1含n个命题变元的极大项是所有这n个变元或其否定形式恰出现一次所构成的析取式,这样的极大项共有2n个
西安电子科技大学 §1.4.2 主合取范式 软件学院 极大项 含n个命题变元的极大项是所有这n个变元 或其否定形式恰出现一次所构成的析取 式,这样的极大项共有2n个。 设P1 ,P2 ,.,Pn 是按顺序排列的n个不同的命题变元, 由这n个命题变元组成的极大项具有以下形式: PPP n ~ ~ ~ ∨ Λ 21 ∨∨ Pi ~ { Pi ¬Pi 编码为0 编码为1
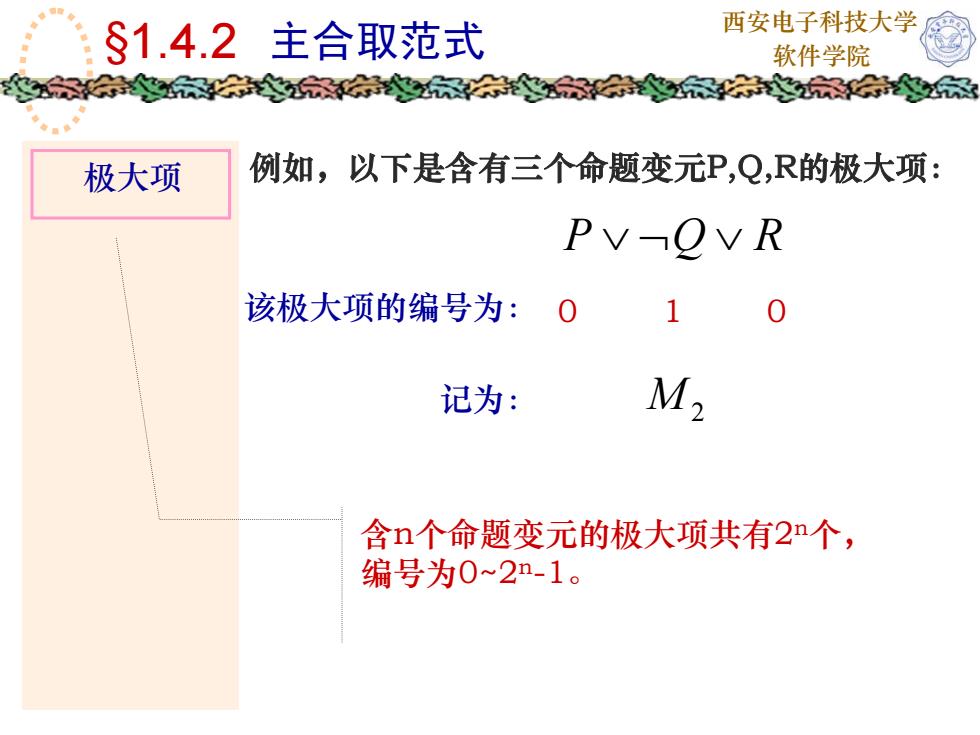
西安电子科技大学S1.4.2主合取范式软件学院茶家家家例如,以下是含有三个命题变元P,Q,R的极大项:极大项PV-QVR该极大项的编号为:001M2记为:含n个命题变元的极大项共有2n个,编号为0~2n-1
西安电子科技大学 §1.4.2 主合取范式 软件学院 极大项 含n个命题变元的极大项共有2n个, 编号为0~2n-1。 例如,以下是含有三个命题变元P,Q,R的极大项: ∨ ¬ ∨ RQP 该极大项的编号为: 0 1 0 记为: M2