西安电子科技大学离散数学软件学院第二篇集合论第3章集合与关系第13课时23.1集合及其运算第14课时一3.2二元关系第15课时3.3集合上的二元关系及其特性第16课时3.4关系的闭包运算第17-18课时3.5等价关系第19-20课时3.6序关系
西安电子科技大学 离散数学 软件学院 第二篇 集合论 第13课时 3.1 集合及其运算 第3章 集合与关系 3.4 关系的闭包运算 3.2 二元关系 3.5 等价关系 第14课时 第16课时 第17-18课时 第15课时 3.3 集合上的二元关系及其特性 第19-20课时 3.6 序关系

西安电子科技大学S3.3.1集合上的二元关系软件学院集合A与A的笛卡儿积A×A的子集,称集合A上的元关系:为集合A上的二元关系。集合上二元关系的前域和陪域是同一个集合
西安电子科技大学 集合上的二元关系 软件学院 集合A上的二 元关系: 集合A与A的笛卡儿积A×A的子集,称 为集合A上的二元关系。 集合上二元关系的前域和陪域是同一个集合 §3.3.1
西安电子科技大学S3.3.1集合上的二元关系软件学院教家教家家教乐家办{马琳,王皓,王励{冯琳,王皓,王励X勤,孔令辉,刘国勤,孔令辉,刘国正,闫森,秦志正,闫森,秦志A:国家乒乓球男队A:国家乒乓球男队A与A笛卡儿积总共有7×7=49个序偶R={,,}国家乒乓球男子双打队
西安电子科技大学 软件学院 R={,,} 国家乒乓球男子双打队 {马琳,王皓,王励 勤,孔令辉,刘国 正,闫森,秦志戬 } A:国家乒乓球男队 {马琳,王皓,王励 勤,孔令辉,刘国 正,闫森,秦志戬 } A:国家乒乓球男队 A与A笛卡儿积总共有7×7=49个序偶 §3.3.1 集合上的二元关系

西安电子科技大学S3.3.1集合上的二元关系软件学院A上特殊的R=Φ空关系:二元关系全域关系:R=AXAA上的相等关系:IA={|xEA}
西安电子科技大学 软件学院 A上特殊的 二元关系 空关系: 全域关系: A上的相等关系: §3.3.1 集合上的二元关系

西安电子科技大学S3.3.1集合上的二元关系软件学院例题设A=1,2,34,A上的二元关系R=[la整除 b}(a)写出关系R中的所有序偶;(b)给出关系R的关系矩阵MR;c)画出关系R的关系图。解答:R=[,,,,,,, }14230021130004000
西安电子科技大学 软件学院 【例题】设A={1,2,3,4},A上的二元关系 (a)写出关系R中的所有序偶; (b)给出关系R的关系矩阵MR ; (c)画出关系R的关系图。 §3.3.1 集合上的二元关系 解答: R={, , , , , , , } ⎥⎥⎥⎥⎦⎤ ⎢⎢⎢⎢⎣⎡ 1000 0100 1010 1111 1 2 3 4 1 2 3 4
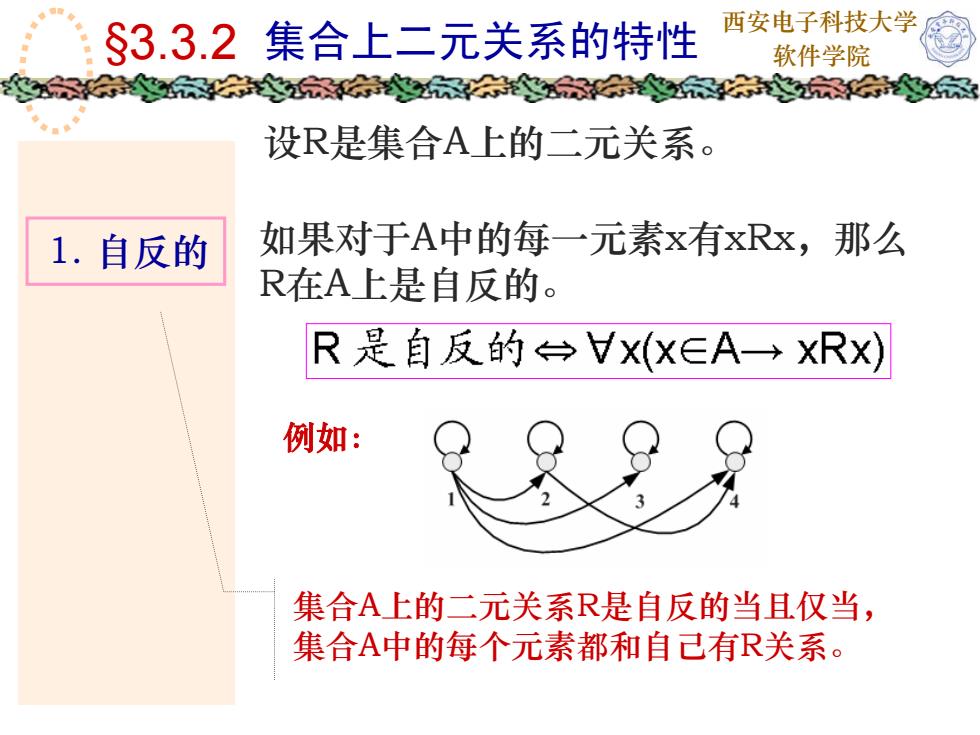
西安电子科技大学$3.3.2集合上二元关系的特性软件学院设R是集合A上的二元关系。如果对于A中的每一元素x有xRx,那么1.自反的R在A上是自反的。R是自反的台Vx(xEA一→xRx)例如:集合A上的二元关系R是自反的当且仅当集合A中的每个元素都和自己有R关系
西安电子科技大学 软件学院 设R是集合A上的二元关系。 如果对于A中的每一元素x有xRx,那么 R在A上是自反的。 1. 自反的 集合A上的二元关系R是自反的当且仅当, 集合A中的每个元素都和自己有R关系。 §3.3.2 集合上二元关系的特性 例如:
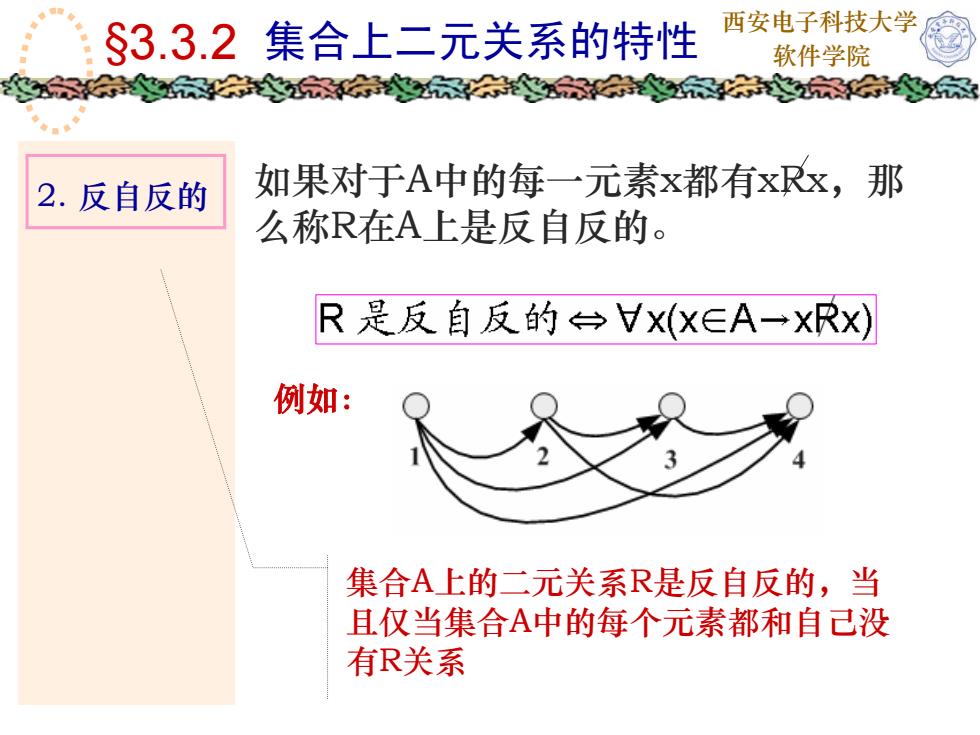
西安电子科技大学S3.3.2集合上二元关系的特性软件学院如果对于A中的每一元素x都有xRx,那2. 反自反的么称R在A上是反自反的。R是反自反的Vx(xEA→xRx)例如:-集合A上的二元关系R是反自反的,当且仅当集合A中的每个元素都和自己没有R关系
西安电子科技大学 软件学院 2. 反自反的 如果对于A中的每一元素x都有xRx,那 么称R在A上是反自反的。 集合A上的二元关系R是反自反的,当 且仅当集合A中的每个元素都和自己没 有R关系 §3.3.2 集合上二元关系的特性 例如:

西安电子科技大学$3.3.2集合上二元关系的特性软件学院家表2.1A上二元关系的特性自反的。反自反的定义任取XEA,有ER任取xEA,有RIA≤R集合RnIA=Φ关系图·图中每个结点都有自回路图中每个结点都没有自回路主对角线上全为0关系矩阵主对角线上全为1
西安电子科技大学 §3.3.2 集合上二元关系的特性 软件学院
西安电子科技大学$3.3.2集合上二元关系的特性软件学院是否有R既是自反的,文是反自反的?空集Φ上的空关系是否有R既不是自反的,文不是反自反的?R的关系图上,有的结点上有自回路,有的结点上没有自回路例如:OO-42
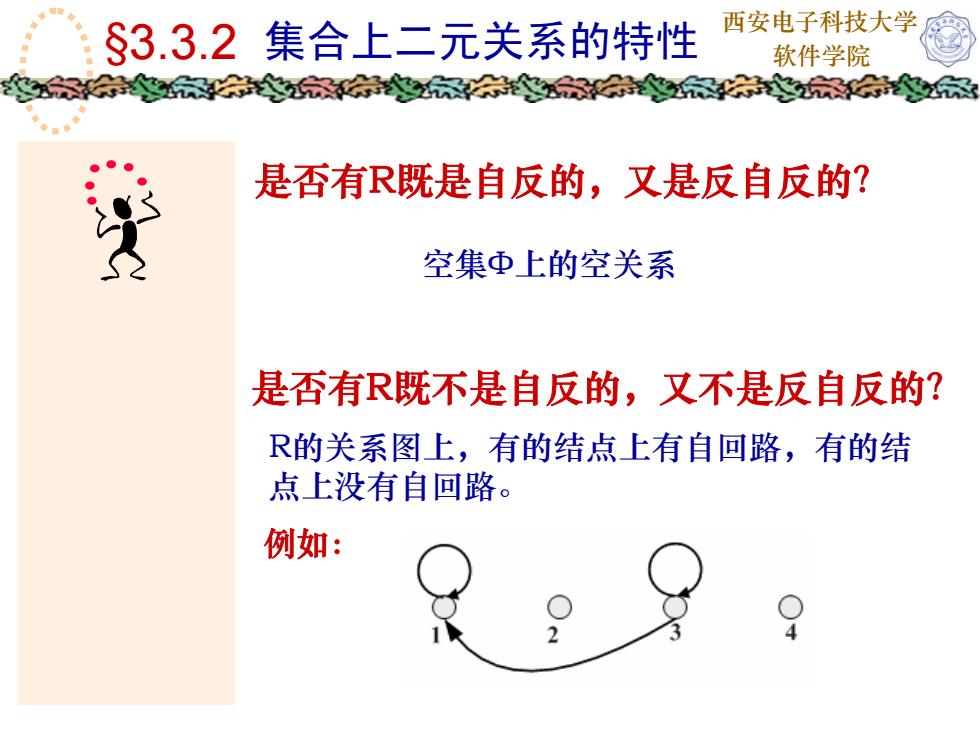
西安电子科技大学 软件学院 是否有R既是自反的,又是反自反的? §3.3.2 集合上二元关系的特性 是否有R既不是自反的,又不是反自反的? 空集Φ上的空关系 R的关系图上,有的结点上有自回路,有的结 点上没有自回路。 例如:
西安电子科技大学S3.3.2集合上二元关系的特性软件学院家如果对于A中的每一对元素x,y,若有xRy,3.对称的则必有yRx,那么称R在A上是对称的。R是对称的VxVy(xEA^yEA^xRy-→yRx)例如:集合A上的二元关系R是对称的,当且仅当若x与y有R关系,则y与x也有R关系
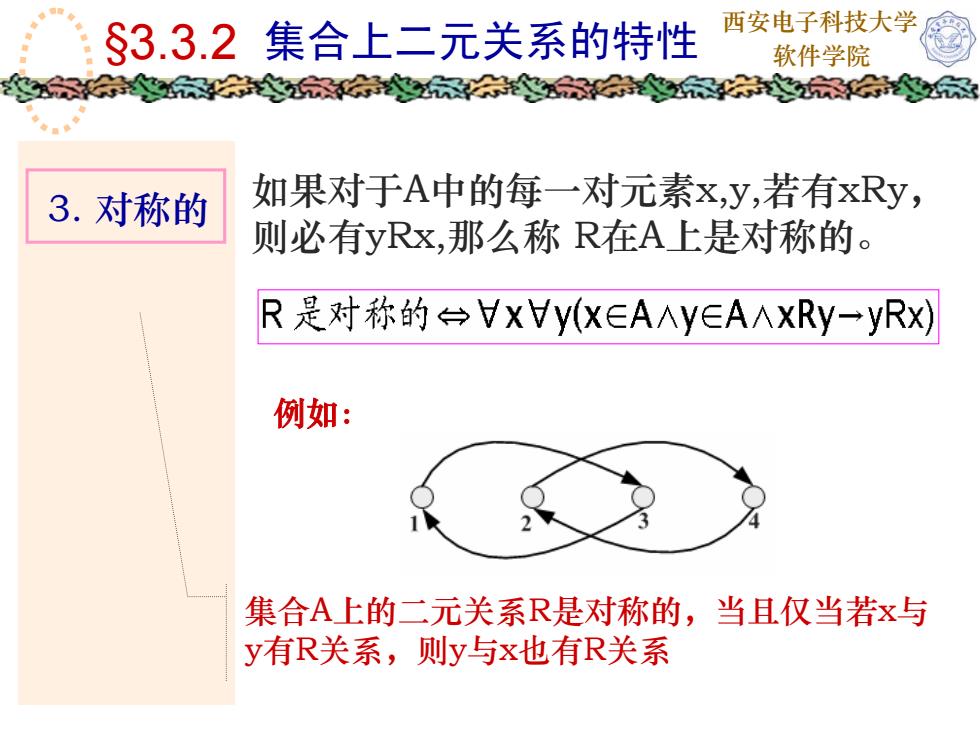
西安电子科技大学 软件学院 如果对于A中的每一对元素x,y,若有xRy, 则必有yRx,那么称 R在A上是对称的。 3. 对称的 集合A上的二元关系R是对称的,当且仅当若x与 y有R关系,则y与x也有R关系 §3.3.2 集合上二元关系的特性 例如: