西安电子科技大学离散数学软件学院第四篇图论第6章图论第27-28课时6.1图的基本概念一第29课时一6.2 路径与回路第30课时→6.3图的矩阵表示第31-32课时6.4欧拉图与汉密尔顿图第33课时6.5平面图之第34课时→6.6图的着色第35—36课时6.7树入6.8图的应用第37-38课时
西安电子科技大学 离散数学 软件学院 第四篇 图论 6.1 图的基本概念 第6章 图论 6.4 欧拉图与汉密尔顿图 6.2 路径与回路 6.5 平面图 第29课时 第33课时 第30课时 6.3 图的矩阵表示 第34课时 6.6 图的着色 第31-32课时 第35-36课时 6.7 树 第27-28课时 第37 -38课时 6.8 图的应用

西安电子科技大学$6.6.1[图着色的基本概念软件学院家图G正常着色是指对G中的每个结点指定一种图的色数颜色,使得没有两个邻接的结点着相同的颜色。如果可以用k种不同的颜色给图C正常着色,则称G是可k-着色的。对图G正常着色所需要的最少的颜色数,称为C的顶着色数(简称为色数),记为(C)。色数为k的图称为k色图
西安电子科技大学 图着色的基本概念 软件学院 图的色数 §6.6.1

西安电子科技大学$6.6.1图着色的基本概念软件学院教家教家用韦尔奇·鲍威尔法可以用最少的颜色数对任意图G进行正常着色,该方法的步骤如下:(1)将图G中的结点按度数递减的次序进行排列;(如果有相同度数的结点,这种排列是不唯一的。)(2)用一种与已着色结点所着颜色不同的新的颜色C对排列最靠前的尚未着色的结点着色,并按排列次序,对与前面已着上颜色C的结点不邻接的每一结点着同样的颜色C;(3)反复重复步骤(2),直到所有结点全部着上颜色为止。#整个过程所用的颜色数即为该图的色数
西安电子科技大学 §6.6.1 图着色的基本概念 软件学院
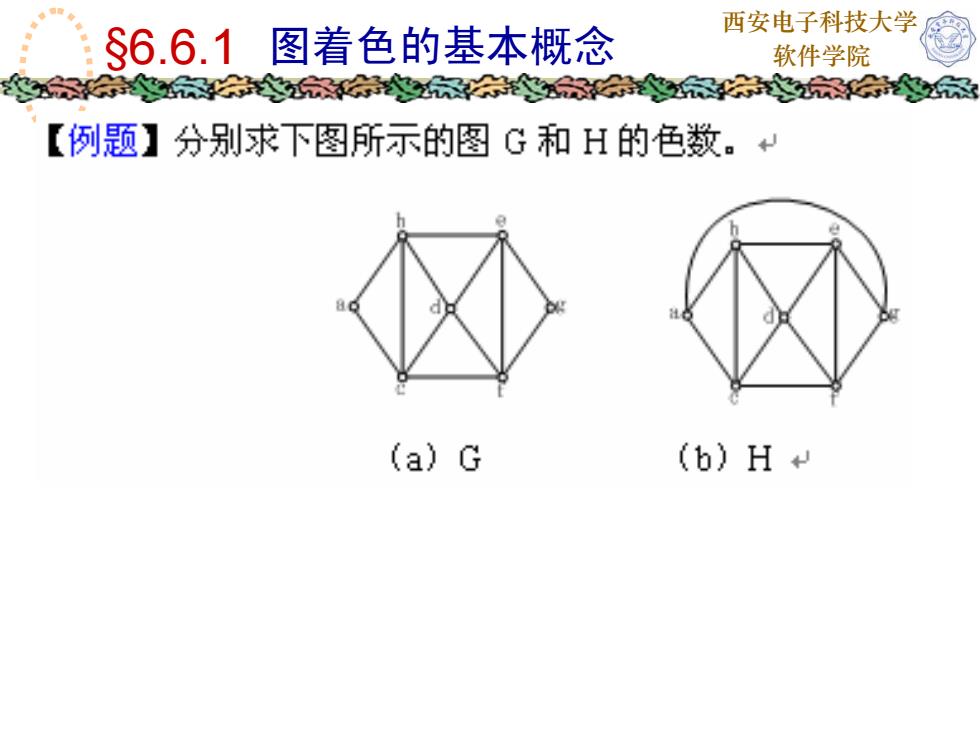
西安电子科技大学庭$6.6.1图着色的基本概念软件学院家家务【例题】分别求下图所示的图G和H的色数。(a) G(b) H t
西安电子科技大学 §6.6.1 图着色的基本概念 软件学院
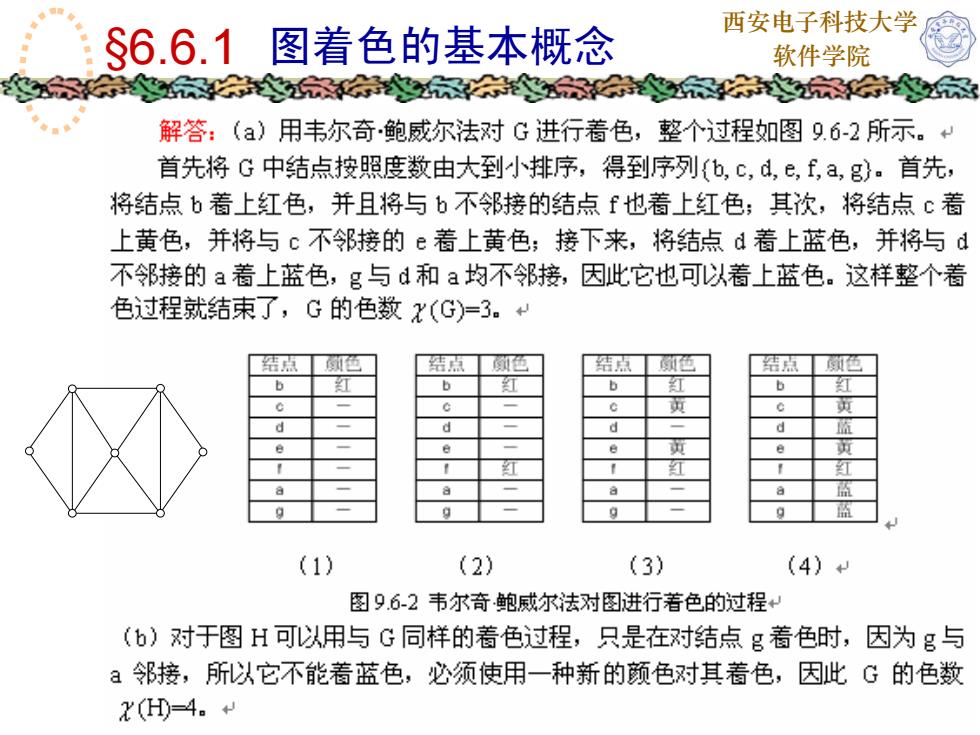
西安电子科技大学$6.6.1图着色的基本概念软件学院解答:(a)用韦尔奇·鲍威尔法对G进行着色,整个过程如图9.6-2所示。+首先将G中结点按照度数由大到小排序,得到序列(b,c,d,e,f,a,g)。首先,将结点b看上红色,并且将与b不邻接的结点f也看上红色;其次,将结点c看上黄色,并将与c不接的e着上黄色:接下来,将结点d着上蓝色,并将与d不邻接的a着上蓝色,g与d和a均不邻接,因此它也可以着上蓝色。这样整个着色过程就结束了,G的色数x(G)=3。+结点结点颜色结点结点飘色颜色颜色H42AL黄英c3A美2红A0蓝(2)(3)(1)(4) 图9.6-2韦尔奇·鲍威尔法对图进行着色的过程+(b)对于图H可以用与G同样的着色过程,只是在对结点g着色时,因为g与a邻接,所以它不能着蓝色,必须使用一种新的颜色对其着色,因此G的色数X(H)-4+
西安电子科技大学 §6.6.1 图着色的基本概念 软件学院

西安电子科技大学店$6.6.1图着色的基本概念软件学院【定理】任何图G均满足(G)≤△(G)+1。证明:设图G中结点的最大度等于k,构造G的一个k十1种颜色的正常着色。对于图G中度数最大的结点V,由于它邻接的结点个数最大为k,若这k个结点均着上了不同的颜色,那么也可以用第k+1种颜色对V进行正常着色
西安电子科技大学 §6.6.1 图着色的基本概念 软件学院 证明:设图G中结点的最大度等于k,构造G的一个k+1种 颜色的正常着色。 对于图G中度数最大的结点v,由于它邻接的结点个数最大为 k,若这k个结点均着上了不同的颜色,那么也可以用第k+1 种颜色对v进行正常着色

西安电子科技大学$6.6.1图着色的基本概念软件学院学教家教家家教家【定理】无向图G的色数(G)=2,当且仅当G是一个二部图。证明:若G是二部图,由于G中的结点集V可以划分为两个子集X和Y,且X和Y中的结点间均不邻接。这样,我们可以使用两种颜色,分别对X和Y中结点着色,即得到G的一种正常着色。所以G的色数等于2。若G的色数等于2,那么图G中至少有两个结点和一条边。若我们用A、B两种颜色对G进行正常着色,那么可以将着A的结点和着B的结点是图G的结点集合V的一个划分。并且A中结点内部不可能存在边,同理B中结点内部也不可能存在边。故G是二部图
西安电子科技大学 §6.6.1 图着色的基本概念 软件学院 证明:若G是二部图,由于G中的结点集V可以划分为两个子 集X和Y,且X和Y中的结点间均不邻接。这样,我们可以使 用两种颜色,分别对X和Y中结点着色,即得到G的一种正常 着色。所以G的色数等于2。 若G的色数等于2,那么图G中至少有两个结点和一条边。若 我们用A、B两种颜色对G进行正常着色,那么可以将着A的 结点和着B的结点是图G的结点集合V的一个划分。并且A中 结点内部不可能存在边,同理B中结点内部也不可能存在 边。故G是二部图

西安电子科技大学$6.6.2平面图的着色软件学院教家定理!(四色定理)平面图的色数不超过4。四色定理至今没有简单的理论证明。1976年美国伊利诺斯大学的两位数学家肯尼斯·阿佩尔和沃尔夫冈·黑肯用计算机运行了将近1200小时证明了四色猜想成立。+
西安电子科技大学 §6.6.2 平面图的着色 软件学院

西安电子科技大学S6.6.2平面图的着色软件学院教家茶茶案定理!设G为一个至少具有三个结点的连通简单平面图,则G中必存在结点u满足deg(u)≤5。+证明:(反证法)+假设G中所有结点的次数均大于等于6。+Y因为deg(v)=2e,故2e≥6,所以e≥3v>3v-6。+i-1这与至少具有三个结点的连通简单平面图的每个面至少由3条边围成满足≤3v-6矛盾。口
西安电子科技大学 §6.6.2 平面图的着色 软件学院

西安电子科技大学座$6.6.2平面图的着色软件学院案定理(希伍德五色定理)任一连通简单平面图C-都是可5一看色的。+证明对图G中的结点数进行归纳(a)当/V|≤5时显然成立。(b)假设当/V=k时成立,现证明/V|=k+1时也成立。(c)前面已经证明,G中必然存在结点u满足deg(u)≤5。将结点u从图中册去得到图G-u。由归纳假设知G-u可以用5种中颜色正常着色。现将u放回从而恢复原图G,有两种情况
西安电子科技大学 §6.6.2 平面图的着色 软件学院