
西安电子科技大学离散数学软件学院第四篇图论第6章图论第27-28课时6.1图的基本概念-第29课时6.2路径与回路→第30课时6.3图的矩阵表示第31-32课时6.4欧拉图与汉密尔顿图6.5平面图第33课时V第34课时6.6图的着色第35课时6.7树(1)大之6.8图的应用第37-38课时
西安电子科技大学 离散数学 软件学院 第四篇 图论 6.1 图的基本概念 第6章 图论 6.4 欧拉图与汉密尔顿图 6.2 路径与回路 6.5 平面图 第29课时 第33课时 第30课时 6.3 图的矩阵表示 第34课时 6.6 图的着色 第31-32课时 第35课时 6.7 树(1) 第27-28课时 第37 -38课时 6.8 图的应用

西安电子科技大学$6.7.1 无向树软件学院家连通且无简单回路的无向图称为无向树,简称树。树无向树中度为1的结点称为树叶,度数大于1的结点称为分枝点或内点。仅含一个孤立结点的树称为平凡树。森林无简单回路的无向图称为森林
西安电子科技大学 无向树 软件学院 无向树 §6.7.1 森林

西安电子科技大学$6.7.1 无向树软件学院来定理!给定一个n个结点m条边的无向图T。以下关于T是无向树的定义是等价的。(1)连通且无简单回路。(2)无简单回路且m-n-1。(3)连通且m=n-1。(4)无简单回路,但增加任一新边,得到一条且仅一条基本回路。(5)连通,但删去一条边后便不连通。(n>2)(6)每一对结点之间有且仅有一条基本路径。(n≥2)
西安电子科技大学 §6.7.1 无向树 软件学院

西安电子科技大学$6.7.1 无向树软件学院(1)连通且无简单回路。证明:采用循环论证方法。2)无简单回路且m=n-1。(1) →(2)对树T中的结点数n进行归纳。当n-1时,必有m=0,因此有m-n-1成立。假设当n-k时命题成立,现证明当n=k+1时命题成立。由于树T是连通的且无简单回路,所以在树T中至少有一个度为1的结点V,从T中删除结点及其关联的一条边e,得到k个结点且无简单回路的连通图T-v。根据归纳假设T-v中有k-1条边.现将结点v及其关联的边e放回以而恢复原图T这样T中必含有k+1个结点和k条边,满足公式m-n-1。所以树是无简单回路且m-n-1的图。+
西安电子科技大学 §6.7.1 无向树 软件学院 (1)连通且无简单回路。 (2)无简单回路且m=n-1

西安电子科技大学无向树$6.7.1 天软件学院(2)无简单回路且m=n-1(2) (3)(3)连通且m=n-1。用反证法。假设图T不连通,并设T中有k(k≥2)个连通分支T1,T2,,TkK其中结点数分别为n,m,…,n,边数分别为m,m2,…m,且有n=n,i1K2m==m,于是有i1SKYm=Z(n-1)=n-k<n-1+m=2-121得出矛盾。所以树T是连通且m-n-1的图。+
西安电子科技大学 §6.7.1 无向树 软件学院 (2)无简单回路且m=n- 1。 (3)连通且m=n-1

西安电子科技大学$6.7.1 无向树软件学院(3)连通且m=n-1。(4)无简单回路,但增加任一新边,得到一条(3) -(4)且仅一条简单回路。首先,证明T中无简单回路,对结点数n进行归纳。+当-1时,m-n-1-0,显然无简单回路。假设当r-k-1时T中无简单回路,现考察当n-k时的情况。此时T中至少有一个结点v的度数为1,因为若k个结点的度数均大于等于2,则T中的边数将不小于k,这与m-n-1矛盾。现将一个度为1的结点v及其关联的一条边从T中删除,得到一个含k-1个结点的图T-V。根据归纳有T-v中无简单回路,再将v及其关联的一条边放回,恢复图T,T也必无简单回路。+其次,证明增加任一新边(И,)得到一个且仅一个基本回路。由于图T是连通的,从到v有一条基本路径P,这条基本路径P与(Vi)就构成了一条简单回路。假设增加边(,)后得到不止一个基本回路,这说明从到vi还有与P不同的另外一条基本路径P,那么P与P将构成的回路中必包含简单回路。这与T中无简单回路矛盾。所以树中无简单回路,但增加任一新边,得到一条且仅一条基本回路。+
西安电子科技大学 §6.7.1 无向树 软件学院 (3)连通且m=n-1。 (4)无简单回路,但增加任一新边,得到一条 且仅一条简单回路

西安电子科技大学店$6.7.1 无向树软件学院家(4)无简单回路,但增加任一新边,得到一条且仅一条简单回路。(5)连通,但删去一条边后便不连通。(n2)(4) →(5)假设图T不连通,则存在两个结点vi和vi间无路径,若T中增加一条新边(vi,vi)不会产生简单回路,这与题设矛盾。由于T中无简单回路,所以删去任一边,图便不连通
西安电子科技大学 §6.7.1 无向树 软件学院 (4)无简单回路,但增加任一新边,得到一条且 仅一条简单回路。 (5)连通,但删去一条边后便不连通。(n≥2) (4)⇒(5) 假设图T不连通,则存在两个结点vi和vj间无路径,若T 中增加一条新边(vi, vj)不会产生简单回路,这与题设矛盾。 由于T中无简单回路,所以删去任一边,图便不连通

西安电子科技大学$6.7.1 无向树软件学院家家(5)连通,但删去一条边后便不连通。(n2)6)每一对结点之间有且仅有一条基本路径。(n≥2)(5) (6)因为T是连通的,所以T中的任意两个不同结点间至少有一条路径,从而也有一条基本路径。若此路径不唯一,则T中含有简单回路,删除此回路上的任一条边不影响图1的连通性,这与题设矛盾。所以这条基本路径是唯一的。所以若树中至少有2个结点数,则每一对结点之间有且仅有一条基本路径。(1)连通且无简单回路。(6) =(1)显然T是连通的。若T中含有简单回路,则回路上任意两点间有两条基本路径,这与题设矛盾
西安电子科技大学 §6.7.1 无向树 软件学院 (5)⇒(6) 因为T是连通的,所以T中的任意两个不同结点间至少 有一条路径,从而也有一条基本路径。若此路径不唯一, 则T中含有简单回路,删除此回路上的任一条边不影响图T 的连通性,这与题设矛盾。所以这条基本路径是唯一的。 所以若树中至少有2个结点数,则每一对结点之间有且仅 有一条基本路径。 (6)⇒(1) 显然T是连通的。若T中含有简单回路,则回路上任意 两点间有两条基本路径,这与题设矛盾。 (5)连通,但删去一条边后便不连通。(n≥2) (6)每一对结点之间有且仅有一条基本路径。(n≥2) (1)连通且无简单回路

西安电子科技大学$6.7.1 无向树软件学院案定理!任一棵非平凡树中至少有两片树叶。证明:设非平凡树T=,|V|=n,IEl=m。由于T是连通的,因此对任意VEV,deg(v)1,且有deg(v)=2m=2(n-1)=2n-2。2F(i)若T中没有树叶,则每个结点的度数均大于等于2。则有:Z deg(v) ≥2n-V这与Zdeg(v)=2n-2矛盾。-(ii)若T中仅有一片树叶,而其它结点的度数均大于等于2。则有: deg(v) ≥2 (m-1)+1=2n-1这与Zdeg(v)=2n-2也矛盾
西安电子科技大学 §6.7.1 无向树 软件学院
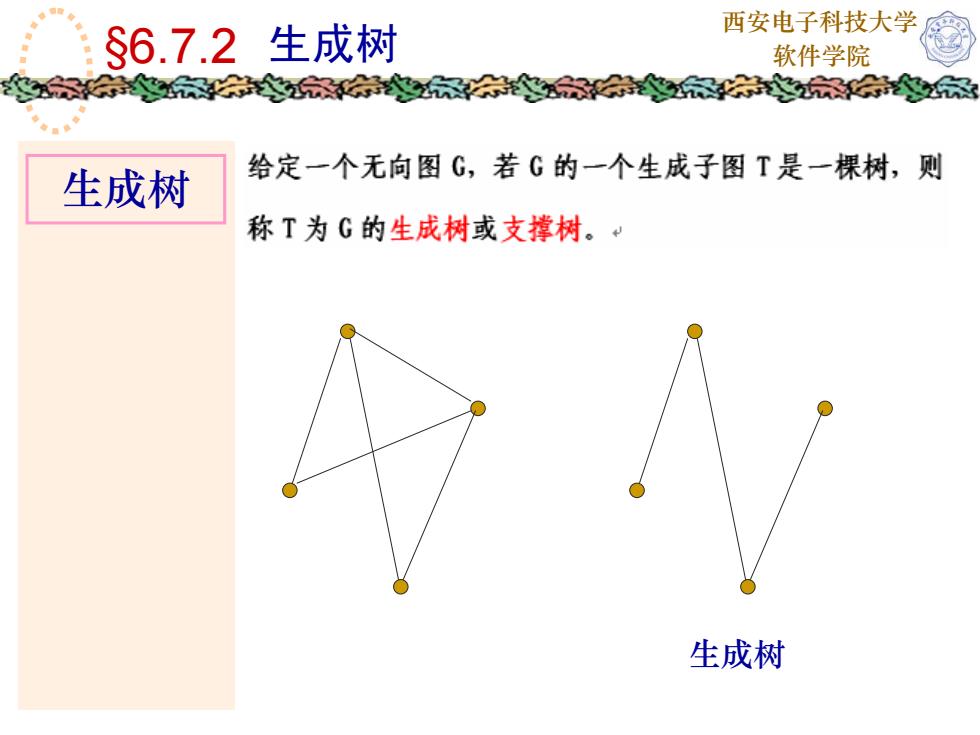
西安电子科技大学$6.7.2 生成树软件学院家教家茶给定一个无向图G,若G的一个生成子图T是一棵树,则生成树称T为G的生成树或支撑树。生成树
西安电子科技大学 生成树 软件学院 生成树 §6.7.2 生成树