
西安电子科技大学离散数学软件学院第二篇集合论第3章集合与关系第13课时V3.1集合及其运算第14课时3.2二元关系第15课时3.3集合上的二元关系及其特性第16课时3.4关系的闭包运算第17-课18时3.5等价关系第19课时3.6序关系(1)7
西安电子科技大学 离散数学 软件学院 第二篇 集合论 第13课时 3.1 集合及其运算 第3章 集合与关系 3.4 关系的闭包运算 3.2 二元关系 3.5 等价关系 第14课时 第16课时 第17-课18时 第15课时 3.3 集合上的二元关系及其特性 第19课时 3.6 序关系(1)

西安电子科技大学S3.6.1偏序集合的定义软件学院家如果集合A上的二元关系R是自反的、反对称偏序和传递的,那么称R为A上的偏序,通常用符号“”表示偏序。称序偶为偏序集合。为了叙述简便,通常用x<y表示x≤y且xty
西安电子科技大学 偏序集合的定义 软件学院 偏序 §3.6.1

西安电子科技大学$3.6.1 1偏序集合的定义软件学院【例题】判断下列集合是否是偏序集合。(a),其中≤是整数集I上的小于等于关系;(b),其中A是集合A的幂集;(c),其中「是自然数集N上的整除关系;(d),其中,其中三3是自然数集N上的模3同余关系;×
西安电子科技大学 §3.6.1 偏序集合的定义 软件学院 【例题】判断下列集合是否是偏序集合。 (a),其中≤是整数集I上的小于等于关系; (b),其中A是集合A的幂集; (c),其中|是自然数集N上的整除关系; (d) ,其中 ,其中≡ 3是自然数集N上的模3同余关系; × × √ √ √

西安电子科技大学哈斯图$3.6.2软件学院然家家对于给定的偏序集合,集合A中元素之间存在一定的大小层次关系,但是它的关系图却无法直观的体现这种层次结构。为此,德国数学家哈斯(Hasse)提出了一种简化的图来表示偏序集合,所以通常称为哈斯图。哈斯图的最大特征是将“较大”的元素画在上方,仅仅在具有相邻大小关系的元素间连线。它其实是原关系对应的盖住关系图。030201
西安电子科技大学 §3.6.2 哈斯图 软件学院 对于给定的偏序集合,集合A中元素之间 存在一定的大小层次关系,但是它的关系图却无法 直观的体现这种层次结构。为此,德国数学家哈斯 (Hasse)提出了一种简化的图来表示偏序集合, 所以通常称为哈斯图。 哈斯图的最大特征是将“较大”的元素画在上 方,仅仅在具有相邻大小关系的元素间连线。它其 实是原关系对应的盖住关系图。 1 2 3 1 2 3

西安电子科技大学哈斯图$3.6.2软件学院家在偏序集合中,元素a,bEA,如果a中,元素x,yEA,X上的盖住集CovA定义为:CovA=( I E≤,,y盖住x)
西安电子科技大学 哈斯图 软件学院 可比 §3.6.2 盖住 在偏序集合中,元素a,b∈A,如果a≼b或 b≼a,称a与b是可比的,否则称它们是不可比 的。 在偏序集合中,元素x,y∈A,x上的盖住集CovA定义为: CovA={ | ∈≼ ,y盖住x}

西安电子科技大学$3.6.2哈斯图软件学院【例题】集合A=(a,b,),偏序集合中,判断A的以下子集是否盖住(a)。(1) ;(2)(b, c;(3) (a, b);(4) (a, b, c)解答:(1)a}盖住の,但e不盖住a:(2){a}与{b,c是不可比较的,因此{b,c}不盖住[a};(3){a,b}盖住[a};(4)因为[a}C{a,b}C(a,b,c},所以a, b,c)不盖住(a)
西安电子科技大学 §3.6.2 哈斯图 软件学院 【例题】集合A={a, b, c},偏序集合中,判断A 的以下子集是否盖住{a}。 (1)∅ ; (2){b, c}; (3){a, b}; (4){a, b, c} 解答: (1){a} 盖住 ∅ ,但∅不盖住{a}; (2){a}与{b, c}是不可比较的,因此{b, c}不盖住{a}; (3){a, b}盖住{a}; (4)因为{a}⊂{a, b}⊂{a,b,c},所以{a, b, c}不盖住 {a}

西安电子科技大学哈斯图$3.6.2P软件学院【例题】A是12的所有因子构成的集合,设|为A上的整除关系,求CovA。解答:A={1,2,3,4,6,12)“|” =[, ,, ,, , ,,,,,,,,,,)。CovA=(, ,, , ,,}
西安电子科技大学 §3.6.2 哈斯图 软件学院 【例题】A是12的所有因子构成的集合,设|为A上的整除 关系,求CovA。 解答:A={1, 2, 3, 4, 6, 12} “|”={, , , , , , , , , , , , , , , , , }。 CovA={, ,, , , , }

西安电子科技大学哈斯图$3.6.2软件学院哈斯图的作图规则如下:(1)用小圆圈表示每个元素;(2)如果xECovA,则在x与y之间用直线连接
西安电子科技大学 §3.6.2 哈斯图 软件学院 哈斯图的作图规则如下: (1)用小圆圈表示每个元素; (2)如果x∈CovA,则在x与y之间用直线连接
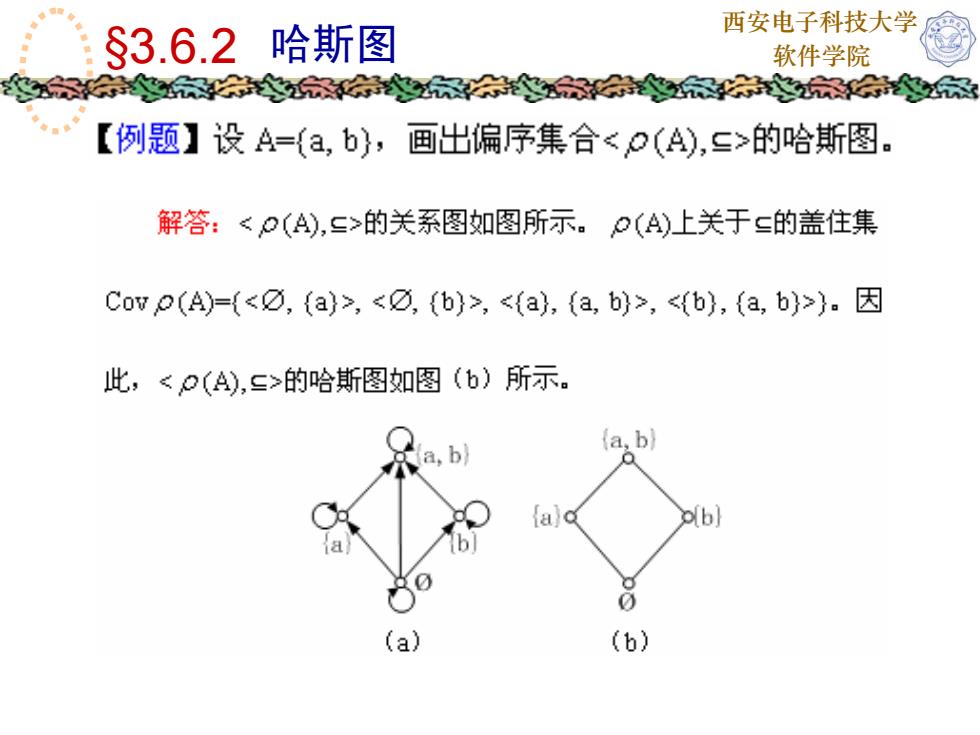
西安电子科技大学哈斯图$3.6.2软件学院-【例题】设A=(a,b),画出偏序集合的哈斯图。解答:的关系图如图所示。P(A)上关于=的盖住集Cov p(A)=(, , , )。 因此,的哈斯图如图(b)所示。(a,b)(a,b)p(b]a0O(b)(a)
西安电子科技大学 §3.6.2 哈斯图 软件学院

西安电子科技大学$3.6.2哈斯图软件学院家哈斯图也可由原偏序的关系图通过以下步骤得到:(1)先画出偏序关系图,并要求所有箭头朝上;(2)移去所有自回路:(3)删除所有可以由传递性导出的边;(4)删除所有箭头
西安电子科技大学 §3.6.2 哈斯图 软件学院 哈斯图也可由原偏序的关系图通过以下步骤得到: (1)先画出偏序关系图,并要求所有箭头朝 上; (2)移去所有自回路; (3)删除所有可以由传递性导出的边; (4)删除所有箭头