西安电子科技大学离散数学软件学院茶第四篇图论第6章图论第27-28课时6.1图的基本概念→第29课时6.2路径与回路A第30课时6.3图的矩阵表示第31-32课时→6.4欧拉图与汉密尔顿图6.5平面图第33-34课时2第35课时6.6图的着色-6.7 树第36-37课时第38课时之6.8图的应用
西安电子科技大学 离散数学 软件学院 第四篇 图论 6.1 图的基本概念 第6章 图论 6.4 欧拉图与汉密尔顿图 6.2 路径与回路 6.5 平面图 第29课时 第33-34课时 第30课时 6.3 图的矩阵表示 第35课时 6.6 图的着色 第31-32课时 第36-37课时 6.7 树 第27-28课时 第38课时 6.8 图的应用

西安电子科技大学路径和回路的定义$6.2.1软件学院家教家家给定图G=,设 vo, Vi, ., VnEV,el, e2 .路径enEE,其中e是关联于结点Vii和v的边。称交替序列VoeiVie2...enVn为连接结点Vo到V,的路径。称Vo为该路径的始点,V为该路径的终点。始点与终点相同的路径。回路
西安电子科技大学 路径和回路的定义 软件学院 路径 §6.2.1 回路

西安电子科技大学路径和回路的定义$6.2.1软件学院茶家家教家若一条路径中经过的所有结点Vo,V1,..,Vn均不相基本路径同,则称该路径为基本路径,亦称作通路或轨。若一条路中经过的所有边e1,e2.,en均不相同,则简单路径称该路径为简单路径或迹
西安电子科技大学 软件学院 基本路径 §6.2.1 简单路径 路径和回路的定义

西安电子科技大学路径和回路的定义$6.2.1软件学院一条回路,除始点与终点相同外其余结点均不相同,基本回路则称该回路为基本回路或圈。一条回路经过的所有边均不相同,则称该回路为简简单回路单回路或闭迹。路径P中所含的边数称为路径P的长度。路径长度
西安电子科技大学 软件学院 基本回路 简单回路 路径长度 §6.2.1 路径和回路的定义
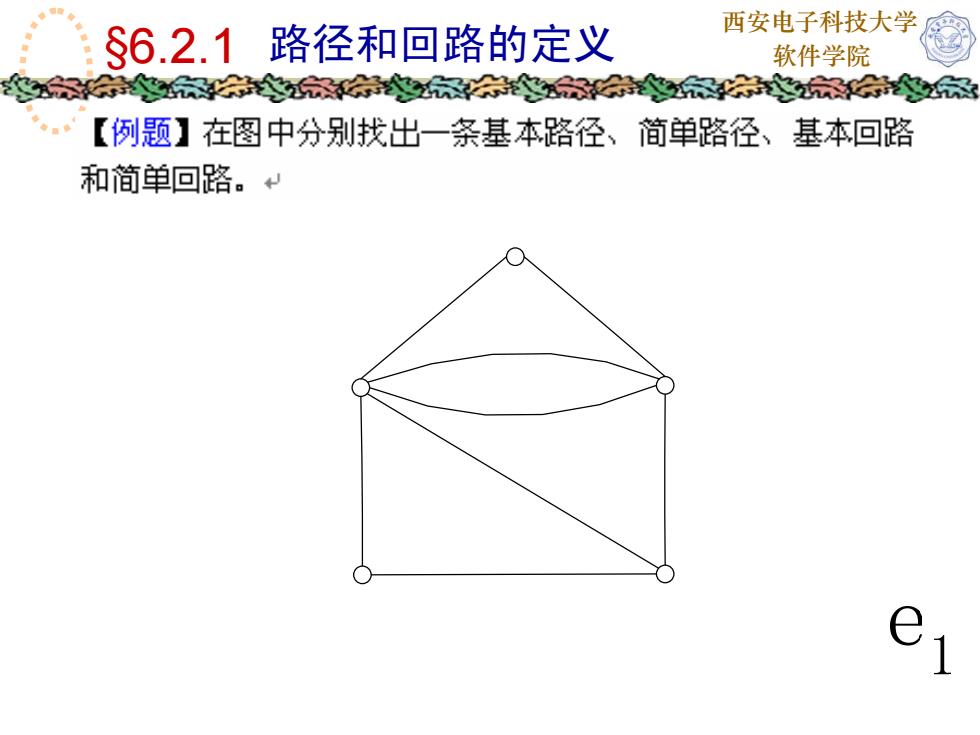
西安电子科技大学S6.2.1路径和回路的定义软件学院家家【例题】在图中分别找出一条基本路径、简单路径、基本回路和简单回路
西安电子科技大学 §6.2.1 路径和回路的定义 软件学院

西安电子科技大学店S6.2.1路径和回路的定义软件学院最「定理!在一个具有Ⅱ个结点的图中,如果从结点vi到Vk存在一条路径,则从结点yi到结点Wis必存在一条长度小于n的基本路径。证明:设从结点V到结点V存在一条路径,该路径上结点的序列为Vi…ViVk。如果这条路径中有p条边,则该路径上必有p+1个结点。若p≥n,则结点数大于等于n+1。根据鸽巢原理,必存在结点Vs,它在序列中不止一次出现,即该路径必有结点序列vivsvsvk。从该路径中去掉从vs到vs之间出现的这些边,所得仍是从v到vk得一条路径,但此路径比原来路径的边数要少。如此重复进行下去,直到删除所有重复的结点,从而得到一条基本路径。由于基本路径的长度等于该路径上的结点数减1,又图G中共有n个结点,故基本路径长度小于等于n-1
西安电子科技大学 §6.2.1 路径和回路的定义 软件学院 证明:设从结点vj到结点vk存在一条路径,该路径上结点的序列为 vj . vi .vk。如果这条路径中有p条边,则该路径上必有p+1个结点。 若p≥n,则结点数大于等于n+1。根据鸽巢原理,必存在结点vs,它 在序列中不止一次出现,即该路径必有结点序列vj .vs .vs.vk。从 该路径中去掉从vs到vs之间出现的这些边,所得仍是从vj到vk得一条路 径,但此路径比原来路径的边数要少。 如此重复进行下去,直到删除所有重复的结点,从而得到一条基本 路径。由于基本路径的长度等于该路径上的结点数减1,又图G中共有n 个结点,故基本路径长度小于等于n-1

西安电子科技大学$6.2.2无向图的连通性软件学院茶家教家家在无向图G中,结点u和结点V之间若存在一条连通路径,则称结点UⅡ和结点V是连通的。在无向图G=中,若任意两结点uVEV都是连通的,则称G是连通图
西安电子科技大学 无向图的连通性 软件学院 连通 §6.2.2

西安电子科技大学$6.2.2无向图的连通性软件学院家家家一个无向图G-中,结点间的连通关系给出连通分支V的一个划分元=Vi,V2.,Vm,使得两个结点vi和vi是连通得当且仅当它们属于同一个VkE元。并且称子图G(Vi),G(V2),…,G(Vm)为图G的连通分支。G的连通分支个数记为α(G)
西安电子科技大学 软件学院 连通分支 §6.2.2 无向图的连通性

西安电子科技大学S6.2.2无向图的连通性软件学院学教家家家教家设无向图G=为连通图,若有点集ViCV,使点割集图G删除了Vi中的所有结点后,所得子图变为非连通的,而删除了Vi的任何真子集后,所得子图仍是连通的,则称Vi为V的一个点割集。若某一个结点构成一个点割集,则称该结点为割点
西安电子科技大学 软件学院 点割集 §6.2.2 无向图的连通性

西安电子科技大学$6.2.2无向图的连通性软件学院家茶茶茶设无向图G=为连通图,若边EiCE,使得从G边割集中删除E中的所有边后所有得子图是不连通的,而删除了E的任一真子集后所得的子图仍是连通的,则称E,为G的一个边割集。若某条边构成边割集,则称该边为割边或桥
西安电子科技大学 无向图的连通性 软件学院 边割集 §6.2.2