
西安电子科技大学离散数学软件学院第一篇数理逻辑第2章谓词逻辑V第7课时1.1 谓词和量词→第8课时1.2谓词公式A第9课时1.3谓词公式的翻译→第10课时1.4谓词演算的永真公式第11课时1.5谓词演算的四个推理规则第12课时1.6谓词逻辑推理及应用V
西安电子科技大学 离散数学 软件学院 第一篇 数理逻辑 第7课时 1.1 谓词和量词 第2章 谓词逻辑 1.4 谓词演算的永真公式 1.2 谓词公式 1.5 谓词演算的四个推理规则 第8课时 第10课时 第11课时 第9课时 1.3 谓词公式的翻译 第12课时 1.6 谓词逻辑推理及应用

西安电子科技大学$2.2.1谓词公式的定义软件学院茶家教家家不含命题联结词的单个谓词A(X1,X2,….,Xn)称为谓词演算的原子公式谓词演算的原子公式。例如: P(x)P(a)Q(x,y)Q(x,a)都是谓词演算的原子公式Q(c,a)TF
西安电子科技大学 软件学院 谓词演算的 原子公式 §2.2.1 谓词公式的定义 例如: P(x) P(a) Q(x,y) Q(x,a) Q(c,a) 都是谓词演算的原子公式 T F

西安电子科技大学谓词公式的定义$2.2.1软件学院办(i)谓词演算的原子公式是谓词公式:谓词公式(i)若A和B是谓词公式,则(-A)(AAB),(AVB),(A一B),(A←B)也是谓词公式;(ii)如果A是谓词公式,X是A中出现的个体变元,则(Vx)A(x)A都是谓词公式:(iv)只有限次应用条款(i)(i)(ii)所得的公式才是谓词公式。例如:P(β)P(×) Q(y)(日x) Q(x,y)都是谓词公式(日y)(Vx)(Q(x,y) →R(y))
西安电子科技大学 谓词公式的定义 软件学院 谓词公式 §2.2.1 例如: P(x) ( ∃x) Q(x,y) ( ∃y)( ∀x)(Q(x,y) →R(y)) 都是谓词公式 } P(x) ∨ Q(y)

西安电子科技大学$2.2.1谓词公式的定义软件学院永家家教茶家教务需要说明的是,要注意条款(ii)的适用条件。例如:由(Vx)P(xy)可以生成(Fy)(Vx)P(x,y),但不能生成(Vx)(Fy)P(x,y)和(x)(Vx)P(x,y)
西安电子科技大学 §2.2.1 谓词公式的定义 软件学院

西安电子科技大学S2.2.2量词的辖域软件学院家家全称量词或存在量词后所跟的变元称为该量词的作用变元作用变元。在量词Vx或Ix的辖域内变元x的一切出现为约约束变元束出现,称这样的变元x为约束变元。自由变元非约束出现的变元称为自由变元。紧跟在量词之后出现的最小子公式称为该量词的量词的辖域辖域
西安电子科技大学 软件学院 作用变元 量词的辖域 量词的辖域 约束变元 自由变元 §2.2.2
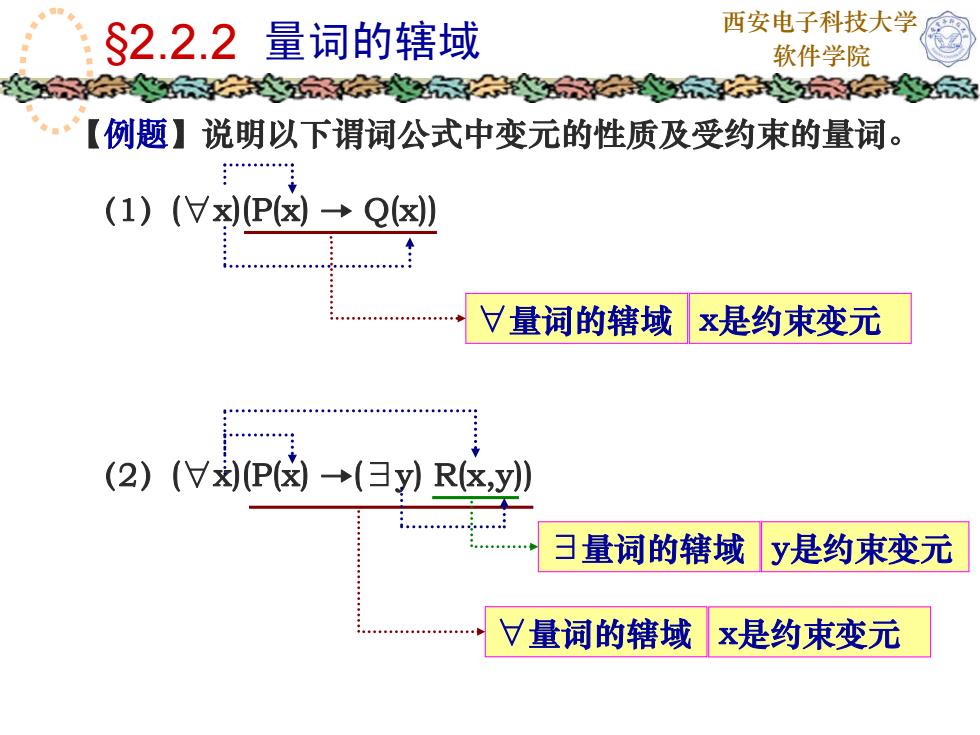
西安电子科技大学S2.2.2量词的辖域软件学院【例题】说明以下谓词公式中变元的性质及受约束的量词。(1) (Vx)(P(β) → Q(×)√量词的辖域x是约束变元(2) (V)(P(β) →(三y) R(x,y)日量词的辖域y是约束变元量词的辖域x是约束变元
西安电子科技大学 §2.2.2 量词的辖域 软件学院 【例题】说明以下谓词公式中变元的性质及受约束的量词。 (1)(∀x)(P(x) → Q(x)) (2)(∀x)(P(x) →(∃y) R(x,y)) ∀量词的辖域 x是约束变元 ∀量词的辖域 ∃量词的辖域 y是约束变元 x是约束变元

西安电子科技大学S2.2.2量词的辖域软件学院【例题】说明以下谓词公式中变元的性质及受约束的量词。(3) (Vx)(Vy)(P(x,y) VQ(y,z) ^ (日y) R(x,y)如果一个变元落入多个量词的辖域内,那么该变元被最靠近它的量词约束。(4) (V×)(P(β) ^(日y) R(x,y) VQ(x,y)两个同名的变元在同一个谓词公式中可以同时以约束变元和自由变元两种形式出现,但它们被认为是不同的个体变元
西安电子科技大学 §2.2.2 量词的辖域 软件学院 【例题】说明以下谓词公式中变元的性质及受约束的量词。 (3)(∀x)(∀y)(P(x,y)∨Q(y,z)∧(∃y) R(x,y)) (4)(∀x)(P(x)∧(∃y) R(x,y)) ∨Q(x,y) 如果一个变元落入多个量词的辖域内,那么该 变元被最靠近它的量词约束。 两个同名的变元在同一个谓词公式中可以同时 以约束变元和自由变元两种形式出现,但它们 被认为是不同的个体变元

西安电子科技大学$2.2.3变元的换名软件学院家家?为什么需要且能够对变元进行换名(1)为避免同一变元符号在谓词公式中既有自由出现,又有约束出现或者出现同一约束变元符号受不同的量词约束的情况,需要对变元进行换名。变元换名的目标是使得同一个变元符号在一个谓词公式中均表示的是相同的个体变元,避免混清。(2)在一个谓词公式中有时候使用的变元符号是无关紧要的:例如:(Vx)P(×) (Vy)P(y)P(×) VQ(y) P(y) VQ(β) P(y) VQ(y)
西安电子科技大学 软件学院 ?为什么需要且能够对变元进行换名 §2.2.3 变元的换名 (2)在一个谓词公式中有时候使用的变元符号是无关紧要的: 例如: ( ∀x)P(x) ⇔ ( ∀y)P(y) P(x)∨Q(y) ⇔P(y)∨Q(x) ⇔/ P(y)∨Q(y) (1)为避免同一变元符号在谓词公式中既有自由出现,又有 约束出现或者出现同一约束变元符号受不同的量词约束的情 况,需要对变元进行换名。 变元换名的目标是使得同一个变元符号在一个谓 词公式中均表示的是相同的个体变元,避免混 淆

西安电子科技大学$2.2.3变元的换名软件学院家变元换名的原则:(1)不改变变元的性质。>变元在换名前后,它是自由变元还是约束变元,这个性质不能发生变化,>约束变元受约束的量词不变。约束变换换名后,应该将量词的作用变元,以及该量词辖域下所有受该量词约束的同名变元一同换名。(2)不改变变元之间的原有的关系。>换名之后是同名的自由变元当且仅当它们在换名之前就是同名的自由变元>受同一量词约束的变元换名后依然是受该量词约束的同名的约束变元
西安电子科技大学 §2.2.3 变元的换名 软件学院 变元换名的原则: (1)不改变变元的性质。 (2)不改变变元之间的原有的关系。 ¾变元在换名前后,它是自由变元还是约束变元,这个性质不能发生变化。 ¾约束变元受约束的量词不变。约束变换换名后,应该将量词的作用变 元,以及该量词辖域下所有受该量词约束的同名变元一同换名。 ¾换名之后是同名的自由变元当且仅当它们在换名之前就是同名的自由变元。 ¾受同一量词约束的变元换名后依然是受该量词约束的同名的约束变元

西安电子科技大学$2.2.3变元的换名软件学院【例题】将谓词公式(x)(P(x)-R(y))VQ(y)中的约束变元×换名。解答:可以将约束变元x换名为Z,从而得到(Vz)(P(z)R(z, y))AQ(x, y)不能将约束变元x换名为y,这样得到(Vy)(P(y)-R(y, y)AQ(x y)因为这会将R(x,y)中的自由变元y变成约束变元,从而改变了整个公式的语义
西安电子科技大学 §2.2.3 变元的换名 软件学院