
雅线性方程的近似解法 ·迭代法收敛性例题 ·一种迭代加速方法一埃特全方法 ·牛顿迭代法 ·孩截法
非线性方程的近似解法 • 迭代法收敛性例题 • 一种迭代加速方法—埃特金方法 • 牛顿迭代法 • 弦截法

非线性方程的近似解法 ·迭代法收敛性例题 ·一种送代加速方法一埃特全方法 ·牛顿迭代法 ·孩截法
非线性方程的近似解法 • 迭代法收敛性例题 • 一种迭代加速方法—埃特金方法 • 牛顿迭代法 • 弦截法

定理1 p(x),x∈[a,b]若满足: 1、a≤p(x)≤b,x∈[a,b] 2、p(x)可导,且存在正数L<1, 使得对任意的x,有 p'(x)≤L 则有: 1、存在唯一的点x*,使得x*=p(x*) 2、x,∈a,b迭代收敛,且有误差估计 s,k刘
(x), x[a,b] 若满足: 1、 a (x) b, x[a,b] 则有: 1、存在唯一的点 x*,使得x* =(x*) 2、 x a,b 0 迭代收敛,且有误差估计 1 0 1 * x x L L x x k k − − − 定理1 2、 (x) 可导,且存在正数L<1, '(x) L 使得对任意的x,有

例1:能否用迭代法求解下列方程,如果不能, 试将方程改写成能用迭代法求解的形式。 (1)x=(cosx+sin x)/4; (2)x=4-2 (x∈[1,2]): 解:①:p(x)=(cosx+snx)/4,且x,有 cos x 11 4 2 .能用迭代法直接求解以上方程
试将方程改写成能用迭代法求解的形式。 例1:能否用迭代法求解下列方程,如果不能, ( )。 ; (2) 4 2 [1,2] (1) (cos sin )/ 4 = − = + x x x x x x 2 1 4 1 4 1 4 cos 4 sin 4 sin cos ( ) 1 ( ) (cos sin )/ 4 + + = − − + = = + x x x x x x x x x 解:() ,且 ,有 能用迭代法直接求解以上方程

W (08)= (2).p(x)=4-2',且x∈[1,2] 装熟素(心,)人=心,Wd .lp'(x)=-2*h2≥2n2≈1.386>1 .·以上方程式不能直接用该迭代函数求解。 改写原方程为x=1og,(4-x)则p,(x)=l0g(4-x) 由x∈[1,2]知, -1 h-2 ≈0.721348≤1 ∴.用迭代函数p(x)求解以上方程式时收敛
(2) (x) = 4 − 2 x[1,2] x ,且 x a x a a a a x x ln 1 (log ) ( ) ln = 高等数学: = ( ) = − 2 ln 2 2ln 2 1.386 1 x x 以上方程式不能直接用该迭代函数求解。 log (4 ) ( ) log (4 ) 2 1 2 改写原方程为x = − x ,则 x = − x 0.721348 1 ln 2(4 2) 1 ln 2(4 ) 1 ln 2(4 ) 1 (4 )ln 2 (4 ) ( ) [1,2] 1 − − = − − = − − = 由 知, x x x x x x 用迭代函数1 (x)求解以上方程式时收敛

非线性方程的近似解法 ·迭代法收敛性例题 ·一种迭代加速方法一埃特全方法 ·牛顿迭代法 ·孩截法
非线性方程的近似解法 • 迭代法收敛性例题 • 一种迭代加速方法—埃特金方法 • 牛顿迭代法 • 弦截法
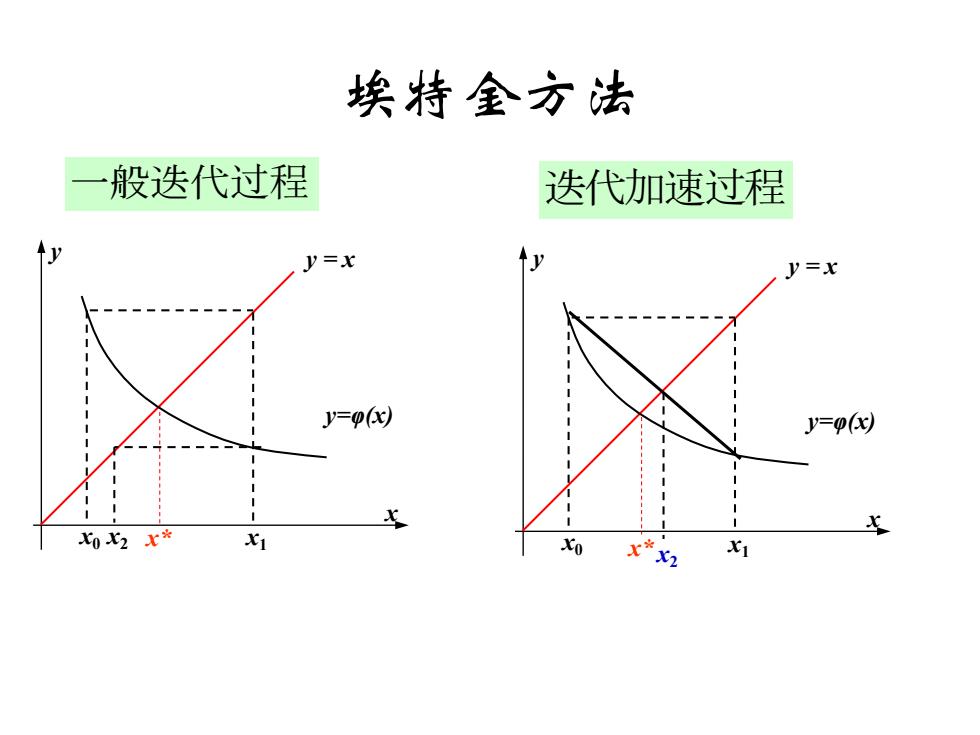
埃特全方法 般迭代过程 迭代加速过程 y=x y=x y=o(x) y=p() 02x* 0 x*x2 x1
埃特金方法 x y y = x x* y=φ(x) x1 x0 x2 x y y = x x* y=φ(x) x1 x0 x2 一般迭代过程 迭代加速过程

埃特全方法 迭代加速过程 过程分析: (1)从x出发先迭代两次,得到 Ax。,x x=p(x)乃x2=p(x) 在y=0(x)上构成两点4(x。,xbB(区,x) x,x,可以看作是临时变量 y-o(x) B(,) (2)求直线AB与y=x的交点(x,x)为 将x 作为第一次的迭代结果。 直线AB方程: x-x=无-x x=p(x)x2=p(x)》 y-x x,-x 迭代方程:x= x无2-x k+ x-2x+ x。-2元+x
埃特金方法 x y y = x x* y=φ(x) x0 x1 迭代加速过程1 x ( , ) 0 1 A x x ( , ) 1 2 B x x 过程分析:( ) ( ) (1) 1 0 2 1 0 x x x x x = , = 从 出发先迭代两次,得到 ( ) ( , ) ( , ) 0 1 1 2 在y = x 上构成两点A x x ,B x x 将 作为第一次的迭代结果。 求直线 与 的交点 , 1 1 1 (2) ( , ) x AB y = x x x x1 ,x2 可以看作是临时变量 2 1 1 0 1 0 AB x x x x y x x x − − = − − 直线 方程: 0 1 2 2 0 2 1 1 x 2x x x x x x − + − 迭代方程: = − + − = = = + 1 2 2 2 1 1 1 2 1 2 ( ) ( ) x x x x x x x x x x x k k k k ,

例1: 灭=p(x)为x2=p(区)》 用埃特金方法求方程2+x-4=0的根 x玉2一 (初值x。=1)。 x-2x+x, 解:将方程改写成达代格式X=h(4一 )取x,=1 第1次选代:正-(4-)=05493L.=号M4-05493)=0.61929 得到:x= x元2-x2 1×0.61929-0.54931 =0.60988 x。-2x+x,1-2×0.54931+0.61929 1 1 第2次迭代:元=h(4-0.60988)=0.61043,元=。ln(4-0.61043)=0.61035 2 得到:x,= x2-x 0.60988×0.61035-0.61043 =0.61036 x-2x+x0.60988-2×0.61043+0.61035 x,-x=0.61036-0.61035=0.0001 ∴.可以认为迭代过程已经收敛,将x,作为方程根的近似
− + − = = = + 1 2 2 2 1 1 1 2 1 2 ( ) ( ) x x x x x x x x x x x k k k k , 初值 。 用埃特金方法求方程 的根 例 : ( 1) 4 0 1 0 2 = + − = x e x x x = ln (4 − x) 2 1 解:将方程改写成迭代格式 ln( 4 0.54931) 0.61929 2 1 ln( 4 1) 0.54931 2 1 第1次迭代:x1 = − = ,x2 = − = 0.60988 1 2 0.54931 0.61929 1 0.61929 0.54931 2 2 0 1 2 2 0 2 1 1 = − + − = − + − = x x x x x x 得到:x 取x0 = 1 ln( 4 0.61043) 0.61035 2 1 ln( 4 0.60988) 0.61043 2 1 2 第 次迭代:x1 = − = ,x2 = − = 0.61036 0.60988 2 0.61043 0.61035 0.60988 0.61035 0.61043 2 2 1 1 2 2 1 2 1 2 = − + − = − + − = x x x x x x 得到:x 可以认为迭代过程已经收敛,将 2作为方程根的近似。 2 2 0.61036 0.61035 0.0001 x x x − = − =

埃特金方法的优点 ·比用一般迭代法计算收敛速度要快; ·对某些发散的迭代过程,改用埃特金方法, 有时也能求出方程的根
埃特金方法的优点 • 比用一般迭代法计算收敛速度要快; • 对某些发散的迭代过程,改用埃特金方法, 有时也能求出方程的根