
主要内容 ·欧拉方法(矩形积分) ·梯形法则(梯形积分) ·改进的欧拉方法 ·预报一校正公式 ·龙格一库塔方法
主要内容 • 欧拉方法(矩形积分) • 梯形法则(梯形积分) • 改进的欧拉方法 • 预报—校正公式 • 龙格—库塔方法

考虑一阶常微分方程的初值问题: y dx =f(x,y)x∈[a,b] y(a)=yo 只要f化,y)在a,b]×R上连续,且关于y满足李普 希茨(Lipschit讴)条件,即存在与x,y无关的常数L使 If(x,y)-f(x,y,)川≤Lly-y,| 对任意定义在[a,b]上的y)和y2c)都成立,则上 述初值问题的连续可微解y(x)在4,b1上存在且唯一
考虑一阶常微分方程的初值问题: = = 0 ( ) ( , ) [ , ] y a y f x y x a b dx dy 只要 f (x, y) 在[a, b] R1 上连续,且关于 y 满足李普 希茨(Lipschitz )条件,即存在与 x, y 无关的常数 L 使 对任意定义在 [a, b] 上的 y1 (x) 和 y2 (x) 都成立,则上 述初值问题的连续可微解y(x)在[a, b] 上存在且唯一。 | ( , ) ( , )| | | 1 2 1 2 f x y − f x y L y − y
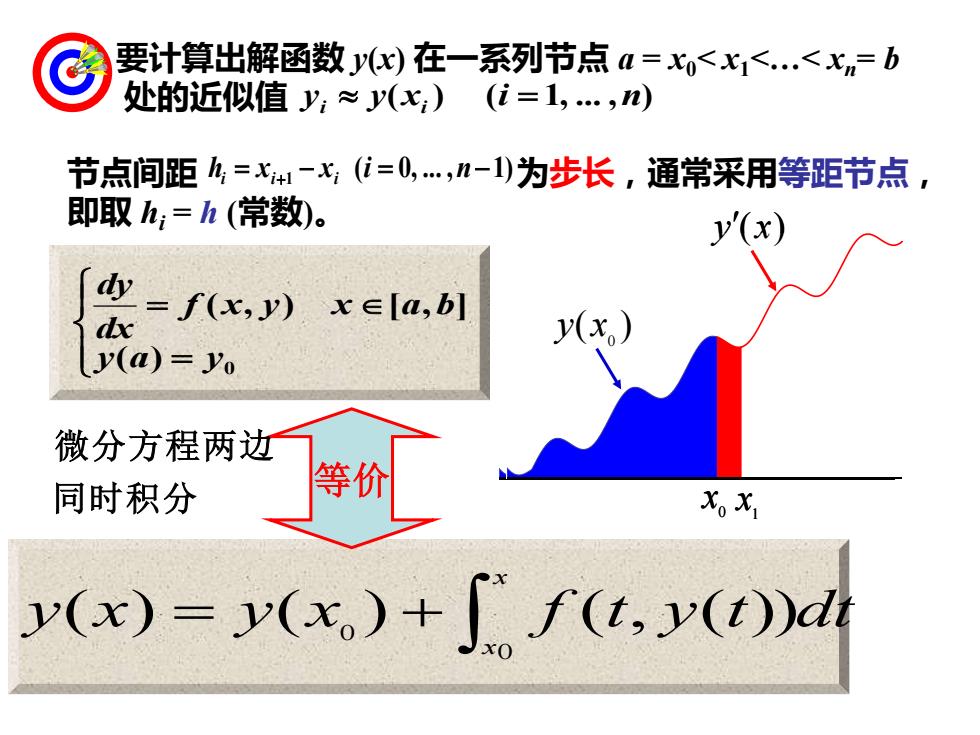
要计算出解函数y()在一系列节点a=x,<x1<.<x=b 处的近似值y:≈y(x:) (i=1,.,m) 节点间距h,=x+-x;(i=0,.,1-1)为步长,通常采用等距节点, 即取h,=h(常数)。 y(x =f(x,y)x∈[a,b dx y(a)=yo 微分方程两边二 同时积分 等价 X。X y(x)=v(x)+f(t,y(t))dr
( ) 0 y x y(x) 0 x 1 x ( ) 0 y x y(x) 0 x 1 x 要计算出解函数 y(x) 在一系列节点 a = x0< x1<.< xn= b 处的近似值 y y(x ) (i 1, . ,n) i i = 节点间距 为步长,通常采用等距节点, 即取 hi = h (常数)。 ( 0, . , 1) hi = xi+1 − xi i = n − = = 0 ( ) ( , ) [ , ] y a y f x y x a b dx dy y x y x f t y t dt x x = + 0 0 ( ) ( ) ( , ( )) 同时积分 等价 微分方程两边
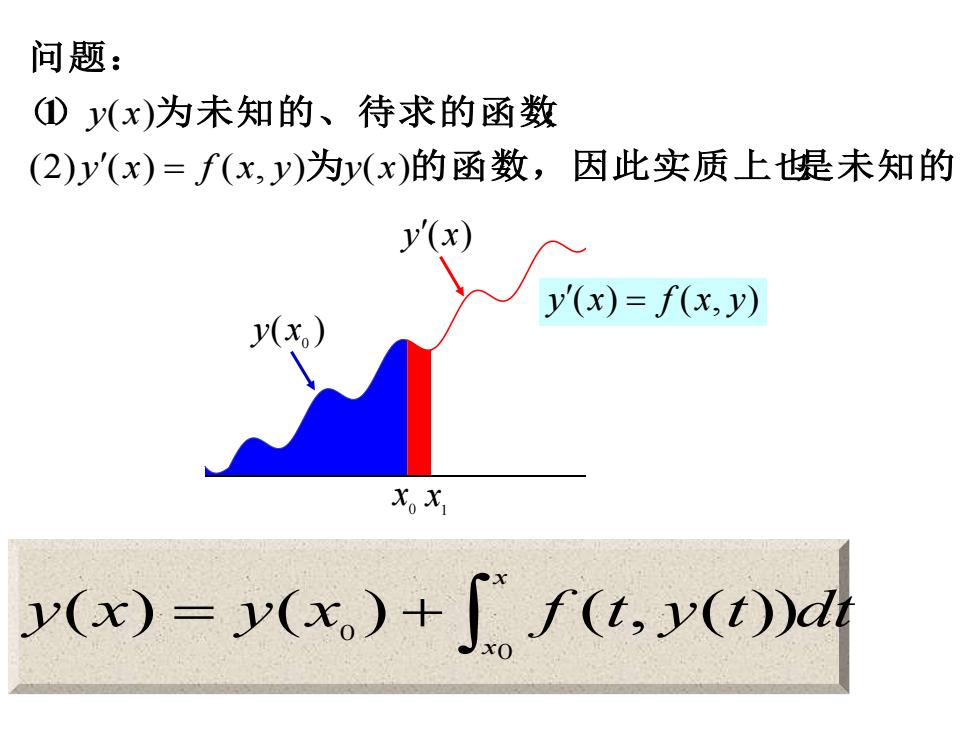
问题: ①y(x)为未知的、待求的函数 (2)y'(x)=f(x,y)为y(x)的函数,因此实质上堤未知的 y'(x) y()=f0x, y(xo) X。X y(x)=x(x)+f(t,y(t))d
为 的函数,因此实质上也是未知的 () 为未知的、待求的函数; 问题: (2) ( ) ( , ) ( ) ( ) y x f x y y x y x = 1 ( ) 0 y x y(x) 0 x 1 x y x y x f t y t dt x x = + 0 0 ( ) ( ) ( , ( )) y(x) = f (x, y)
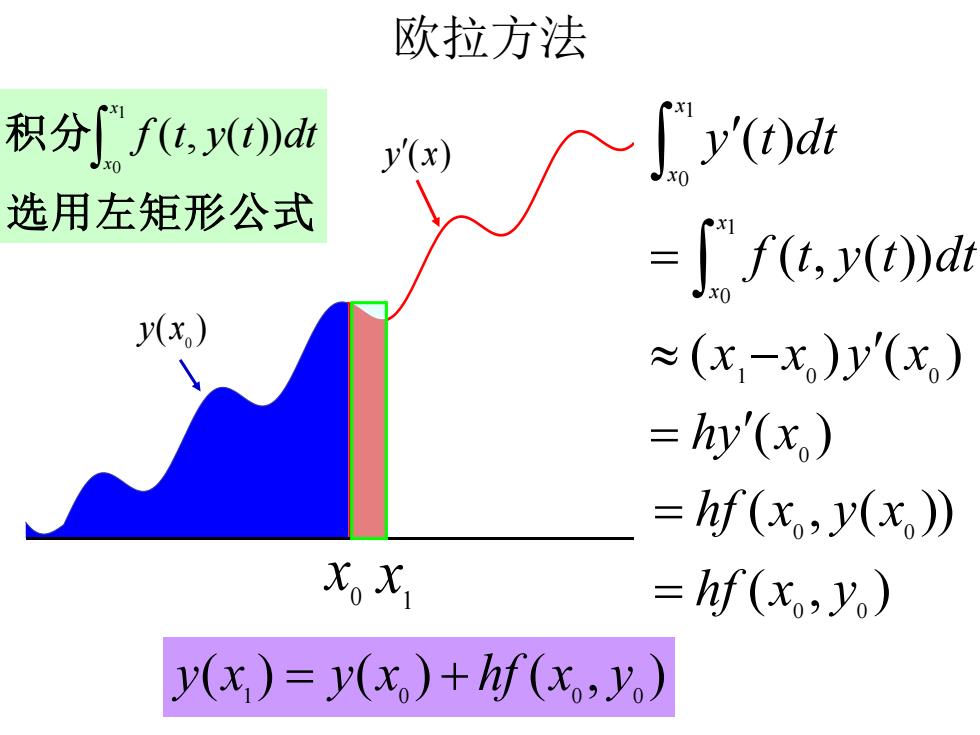
欧拉方法 积分f(t,y(t)d y'(x) 入''()a 选用左矩形公式 =f(uy()》 ≈(x,-x)y'(x) hy'(x) =hf(x,y(x)) XX hf(xo,yo) y(x,)=y(x)+hf(x2 y)
( ) 0 y x y(x) 0 x 1 x 欧拉方法 选用左矩形公式 积分 1 0 ( , ( )) x x f t y t dt ( ) ( ) ( ) ( , ( )) ( ) 0 1 0 0 1 0 1 0 hy x x x y x f t y t dt y t dt x x x x = − = ( , ) ( , ( )) 0 0 0 0 hf x y hf x y x = = ( ) ( ) ( , ) 1 0 0 0 y x = y x + hf x y
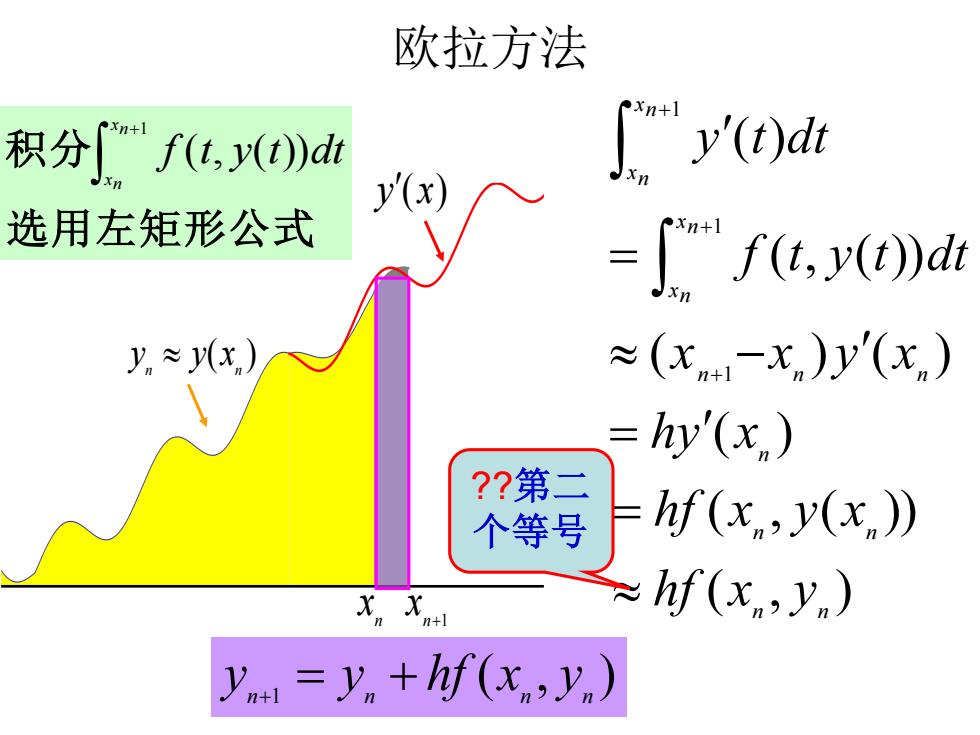
欧拉方法 xn+] 积分f(t,()》d y'(x) 选用左矩形公式 [""f(t,y(t)dt yn≈xn) ≈(xn1-xn)y'(xn) =hy'(x) ??第二 个等号 hf(x,y(x.)) XX hf(x.,y.) y=y.+hf(x,y)
欧拉方法 ( ) n n y y x y(x) n x n+1 x 选用左矩形公式 积分 +1 ( , ( )) x n x n f t y t dt ( ) ( ) ( ) ( , ( )) ( ) 1 1 1 n n n n x n x n x n x n hy x x x y x f t y t dt y t dt = − = + + + ( , ) ( , ( )) n n n n hf x y hf x y x = ??第二 个等号 ( , ) n 1 n n n y = y + hf x y +

y(x)=y(x,)+hf(x2y) 欧拉方法截断误差分析 假设(x)=y. y(x)=y(x,)+hy'(x)+O(h) =y(x,)+hf(x y(x,))+O(h) =y,+hf(x,y)+O(h) y=y.+hf(xy) y(x)-y1=O(h2) 精度较差
欧拉方法截断误差分析 ( ) ( ) ( , ) n 1 n n n y x = y x + hf x y + n n 假设y(x ) = y ( , ) ( ) ( ) ( , ( )) ( ) ( ) ( ) ( ) ( ) 2 2 2 1 y hf x y O h y x hf x y x O h y x y x hy x O h n n n n n n n n n = + + = + + + = + + ( , ) n 1 n n n y = y + hf x y + ( ) ( ) 2 y x n+1 − yn+1 = O h 精度较差
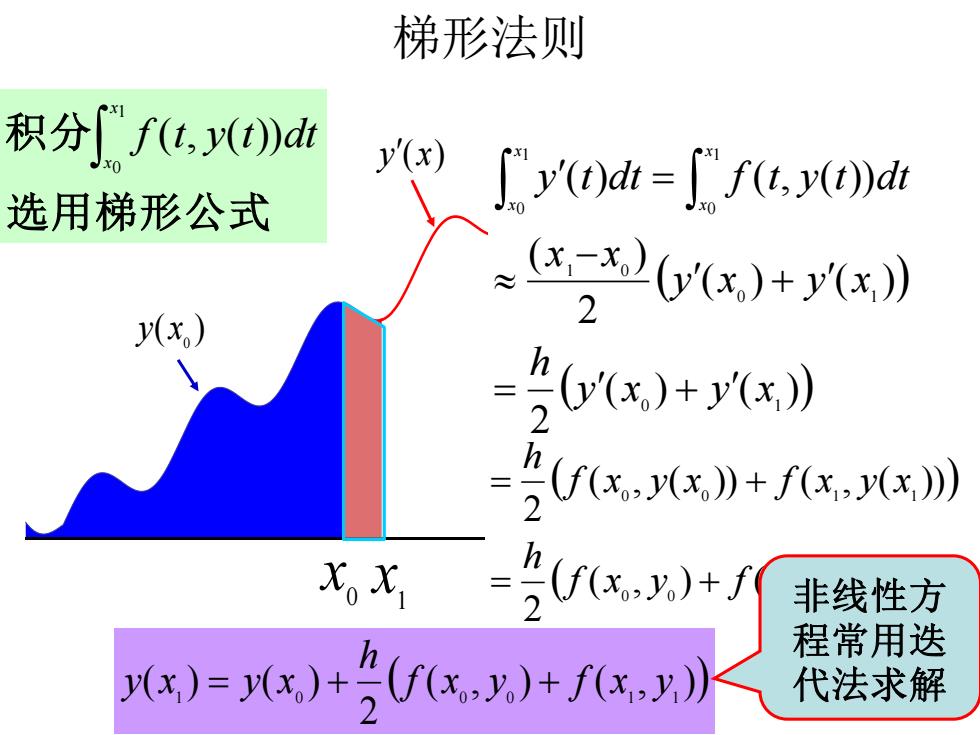
梯形法则 积分f(,y()d y(x) 选用梯形公式 y(Od=[f(t,y()dr 6yx,)+y'x)》 2 y(x.) hyx,)+(x》 ((x,x》+fx,(x川 )(f(x,y)+f 非线性方 )=x)+,)+fx,》 程常用迭 代法求解
( ) 0 y x y(x) 0 x 1 x 梯形法则 ( ) ( ( , ) ( , )) 2 ( , ( )) ( , ( )) 2 0 0 1 1 0 0 1 1 f x y f x y h f x y x f x y x h = + = + 选用梯形公式 积分 1 0 ( , ( )) x x f t y t dt ( ) ( ( ) ( )) 2 ( ) ( ) 2 ( ) ( ) ( , ( )) 0 1 0 1 1 0 1 0 1 0 y x y x h y x y x x x y t dt f t y t dt x x x x = + + − = ( ( , ) ( , )) 2 ( ) ( ) 1 0 0 0 1 1 f x y f x y h y x = y x + + 非线性方 程常用迭 代法求解

梯形法则 积分∫f(t,()》d y(d=f(t,y(dr y'(x) 选用梯形公式 6y(x)+yx》 h6'(x,)+y'x》 5(f(x,y(x》+f(x,y(x) fx,y)+f xX 非线性方 n+ =y+2x,y)+f0. 程常用迭 代法求解
梯形法则 ( ) n n y y x y(x) n x n+1 x ( ) ( ( , ) ( , )) 2 ( , ( )) ( , ( )) 2 1 1 1 + + + + = + n n n n n n n n f x y f x y h f x y x f x y x h 选用梯形公式 积分 +1 ( , ( )) x n x n f t y t dt ( ) ( ( ) ( )) 2 ( ) ( ) 2 ( ) ( ) ( , ( )) 1 1 1 1 1 + + + + + = + + − = n n n n n n x n x n x n x n y x y x h y x y x x x y t dt f t y t dt ( ( , ) ( , )) 2 n+1 = n + n n + n+1 n+1 f x y f x y h y y 非线性方 程常用迭 代法求解

y=y.+fx,y)+fxy) 改进的欧拉方法 y=yn+hf(x,y)(显式欧拉公式) +2x,为)+fxy少》k=012. y=y.+ 优点:精度比较好; 改进的欧拉方法与 缺点:计算量太大。 梯形法则的本质区 别是什么?
改进的欧拉方法 ( ( , ) ( , )) 2 n+1 = n + n n + n+1 n+1 f x y f x y h y y ( ) = + + = + + + + + + ( , ) ( , ) 2 ( , ) ( ) 1 1 ( 1) 1 ( 0) 1 k n n n n n k n n n n n f x y f x y h y y y y hf x y (显式欧拉公式) (k = 0,1,2, ) 优点:精度比较好; 缺点:计算量太大。 改进的欧拉方法与 梯形法则的本质区 别是什么?