西安电子科技大学离散数学软件学院办第二篇集合论第3章集合与关系第13课时V3.1集合及其运算第14课时3.2二元关系X第15课时3.3集合上的二元关系及其特性第16课时→3.4关系的闭包运算3.5等价关系第17-18课时第19-20课时3.6序关系
西安电子科技大学 离散数学 软件学院 第二篇 集合论 第13课时 3.1 集合及其运算 第3章 集合与关系 3.4 关系的闭包运算 3.2 二元关系 3.5 等价关系 第14课时 第16课时 第17-18课时 第15课时 3.3 集合上的二元关系及其特性 第19-20课时 3.6 序关系

西安电子科技大学关系闭包的定义$3.4.1软件学院茶教家家家教家家设R是集合A上的二元关系,R的自反(对闭包称、传递)闭包是满足以下条件的关系R(i)R'是自反的(对称的、传递的);(ii) R'2R;(iii)对于A上的任何自反(对称、传递)关系R",若R"2R,则有R"2R'R的自反、对称、传递闭包分别记为r(R)、s(R) 和t(R)。集合A上的二元关系R的自反(对称、传递)闭包是包含R的最小的自反(对称、传递)关系
西安电子科技大学 关系闭包的定义 软件学院 闭包 §3.4.1 集合A上的二元关系R的自反(对称、传递)闭 包是包含R的最小的自反(对称、传递)关系。 设R是集合A上的二元关系,R的自反(对 称、传递)闭包是满足以下条件的关系R': (i)R'是自反的(对称的、传递的); (ii)R' ⊇R; (iii)对于A上的任何自反(对称、传递) 关系R",若R" ⊇R,则有R" ⊇R'。 R的自反、对称、传递闭包分别记为 r(R) 、s(R) 和t(R)

西安电子科技大学$3.4.2关系闭包的计算软件学院家「定理」设R是集合A上的二元关系,那么有(a)R是自反的当且仅当I(R=R;(b)R是对称的当且仅当s(R)=R(c)R是传递的当且仅当t(R)=R
西安电子科技大学 §3.4.2 关系闭包的计算 软件学院

西安电子科技大学$3.4.2关系闭包的计算软件学院茶教家家家案『定理』设R是集合A上的二元关系,那么有(a) r(R)=RUIA(b) s(R)=RUR-1(c) t(R)=RUR2 U.. URn... = YRii=1
西安电子科技大学 软件学院 (c)t(R)=R∪R2 ∪. ∪Rn. = §3.4.2 关系闭包的计算 『定理』设R是集合A上的二元关系,那么有 Υ ∞ i=1 i R (a)r(R)=R∪IA (b)s(R)=R∪R-1�

西安电子科技大学$3.4.2关系闭包的计算软件学院茶证明:(a)(用自反闭包的定义证明)令R'=RUIA(i)任取xEA,EIA,则ERUIA,故R是自反的。(ii)显然R'2R;(iii)任取A上的自反关系R",且R"2R,现证明R"2R'。任取ER',则有ER或EIA9若ER,则有ER";若EIA,则x=y,又因为R"是自反的,所以ER"。故有R"2R'。由此可知r(R)=R'=RUIA°
西安电子科技大学 §3.4.2 关系闭包的计算 软件学院 证明:(a)(用自反闭包的定义证明) 令R'= R∪IA。 (i)任取x∈A,∈IA,则∈R∪IA,故R'是自反 的。 (ii)显然R'⊇ R; (iii)任取A上的自反关系R",且R"⊇ R,现证明R"⊇R'。 任取∈R' ,则有∈R或∈IA。 若∈R,则有∈R"; 若∈IA,则x=y,又因为R"是自反的,所以∈R"。 故有R"⊇ R'。 由此可知r(R)=R'=R∪IA
西安电子科技大学S3.4.2关系闭包的计算软件学院教家茶家【例题】设A={a,b,c,A上的二元关系R=(,),求r(R)、s(R)和t(R),并分别给出各闭包的关系矩阵和关系图。0000解答:(a)求自反闭包r(R)r(R)=RUIA={, , , , , )。011011110ba
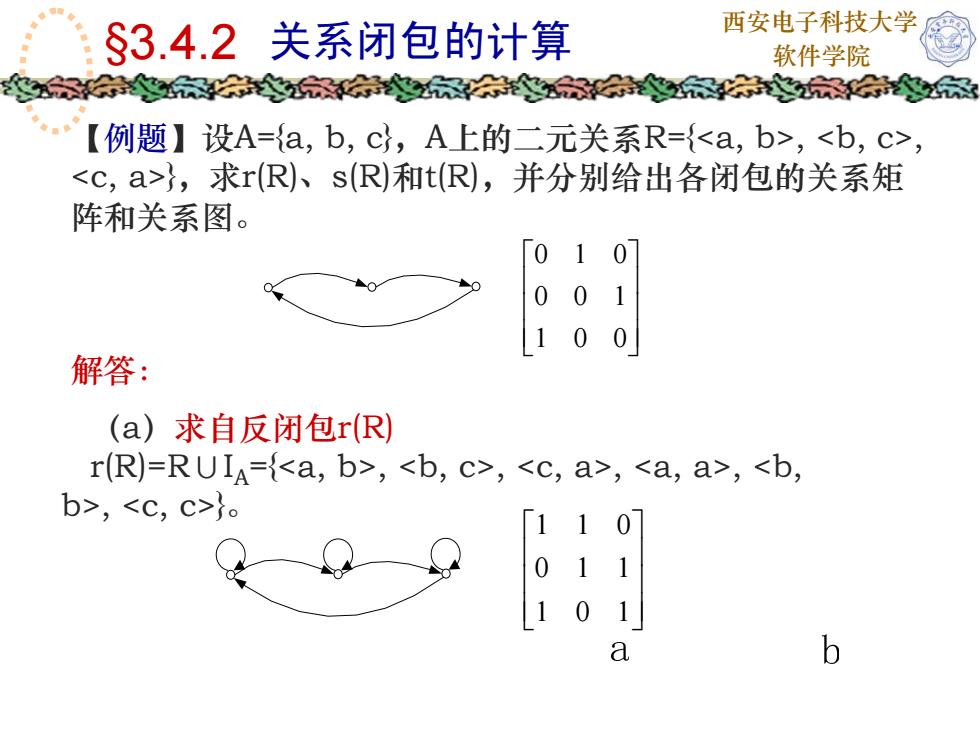
西安电子科技大学 §3.4.2 关系闭包的计算 软件学院 【例题】设A={a, b, c},A上的二元关系R={, , },求r(R)、s(R)和t(R),并分别给出各闭包的关系矩 阵和关系图。 ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ 001 100 010 ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ 101 110 011 (a)求自反闭包r(R) r(R)=R∪I A={, , , , , }。 解答:
西安电子科技大学$3.4.2关系闭包的计算软件学院家(b)求对称闭包s(R)s(R)=RUR-1=(,,, , ,}00
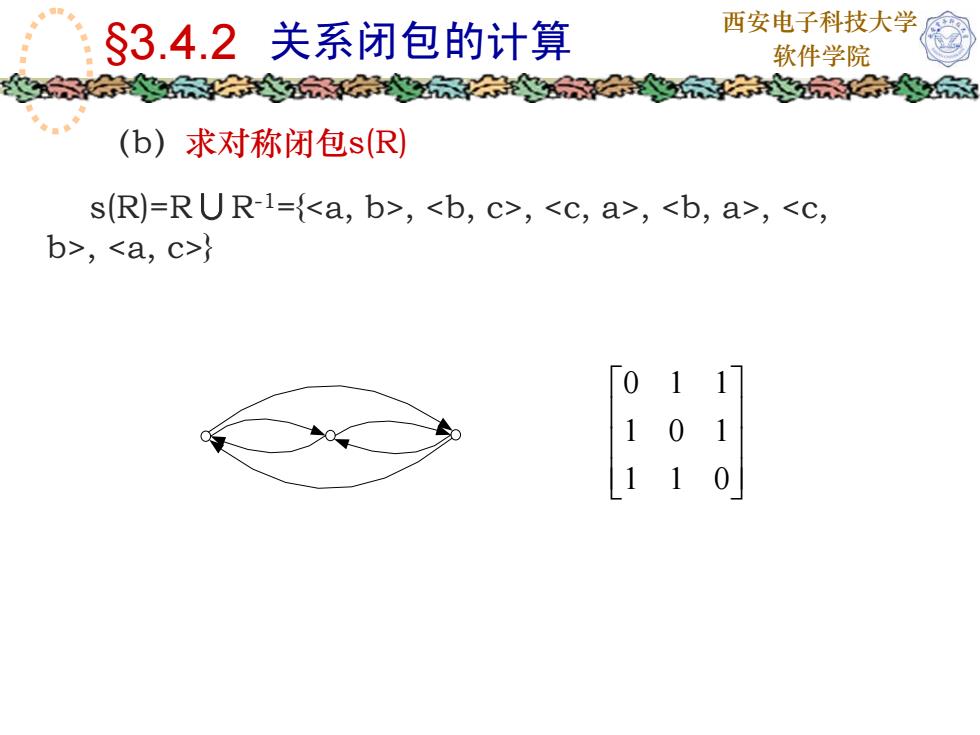
西安电子科技大学 §3.4.2 关系闭包的计算 软件学院 (b)求对称闭包s(R) ⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ 011 101 110 s(R)=R∪R-1={, , , , , }

西安电子科技大学$3.4.2关系闭包的计算软件学院茶(c)求传递闭包t(R)R=(, , }R2=(, ,)R3=(, , )= I=Ro因此有R4=R,R5=R2,·,R3n+1=R,R3n+2=R2,R3n+3=R3...t(R)=RUR2UR3...=RUR2 UR3={, , ,,,,,,}。1111111
西安电子科技大学 §3.4.2 关系闭包的计算 软件学院 (c)求传递闭包t(R) ⎥⎥⎥⎦⎤ ⎢⎢⎢⎣⎡ 111 111 111 R={, , } R2={, , } R3={, , }= IA=R0 因此有R4=R, R5=R2, ., R3n+1=R,R3n+2=R2, R3n+3=R3. t(R)=R∪R2∪R3.=R∪R2 ∪R3={, , , , , , , , }
西安电子科技大学$3.4.2关系闭包的计算软件学院r(R)s(R)RGR所有的边GR所有结点关系图GR加上方向相反上添加自回路的另一条边MR主对角线关系矩阵MRMr并上其转上元素全变1置阵Mr-1
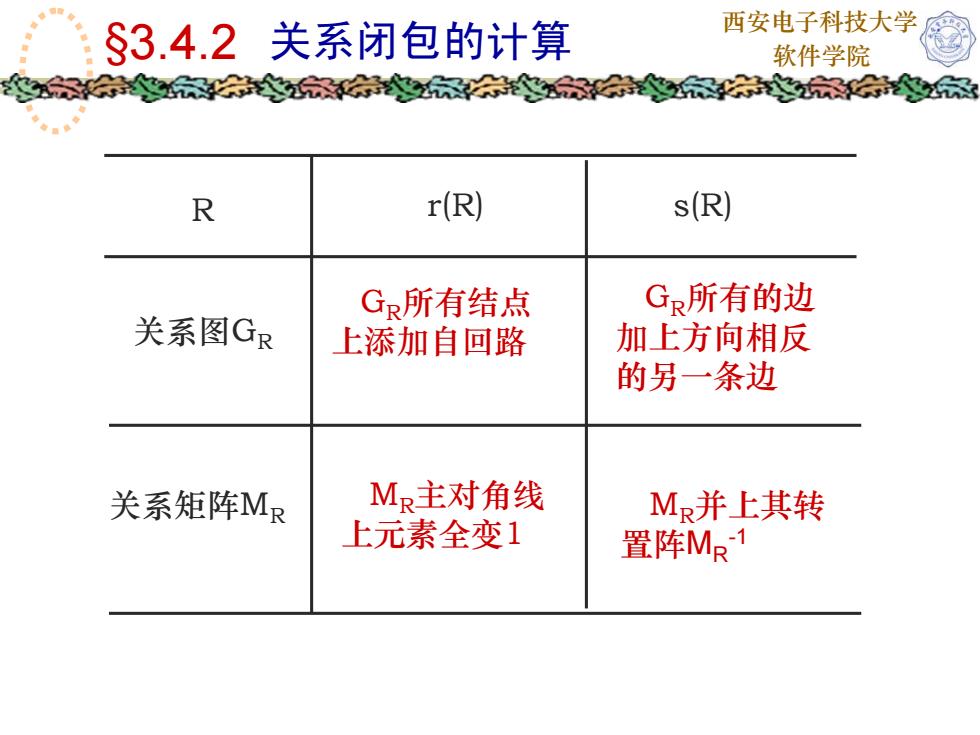
西安电子科技大学 §3.4.2 关系闭包的计算 软件学院 R r(R) s(R) 关系图G R 关系矩阵M R G R所有结点 上添加自回路 G R所有的边 加上方向相反 的另一条边 M R主对角线 上元素全变1 M R并上其转 置阵 M R -1
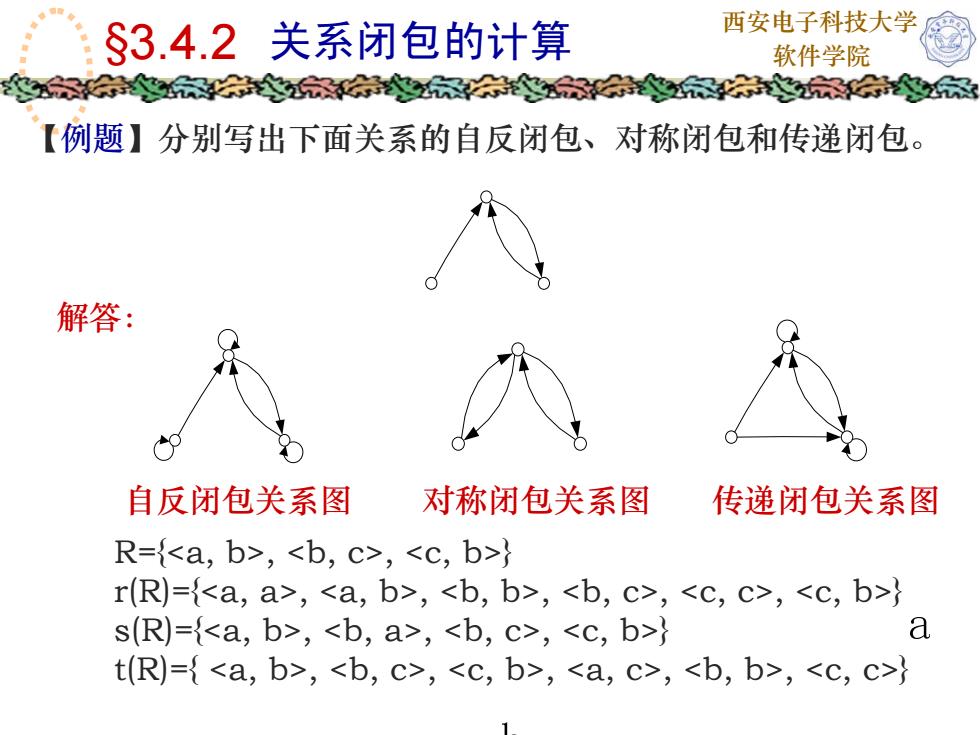
西安电子科技大学S3.4.2关系闭包的计算软件学院【例题】分别写出下面关系的自反闭包、对称闭包和传递闭包。解答:自反闭包关系图传递闭包关系图对称闭包关系图R=(,,)r(R)=(,,,,, )as(R)=(,, ,)t(R)={, ,,, ,)
西安电子科技大学 §3.4.2 关系闭包的计算 软件学院 【例题】分别写出下面关系的自反闭包、对称闭包和传递闭包。 解答: 自反闭包关系图 对称闭包关系图 传递闭包关系图 R={, , } r(R)={, , , , , } s(R)={, , , } t(R)={ , , , , , }