西安电子科技大学离散数学软件学院第四篇图论第6章图论第27课时6.1图的基本概念(1)TA第29课时6.2路径与回路A第30课时6.3图的矩阵表示第31-32课时X6.4欧拉图与汉密尔顿图第33-—34课时6.5平面图?第35课时6.6图的着色-6.7 树第36-37课时第38课时之6.8图的应用
西安电子科技大学 离散数学 软件学院 第四篇 图论 6.1 图的基本概念(1) 第6章 图论 6.4 欧拉图与汉密尔顿图 6.2 路径与回路 6.5 平面图 第29课时 第33-34课时 第30课时 6.3 图的矩阵表示 第35课时 6.6 图的着色 第31-32课时 第36-37课时 6.7 树 第27课时 第38课时 6.8 图的应用

西安电子科技大学$6.1.1图的定义软件学院一个图是一个三元组,其中图V(G)是一个非空的结点(或顶点)集合,E(G)是边集合,(G)是从边集合到结点偶对集合上的函数。+
西安电子科技大学 图的定义 软件学院 图 §6.1.1

西安电子科技大学图的定义$6.1.1软件学院教家家设边e=[u,v],若[u,v]是无序对(u,v),则称e是无向边无向边,e关联的两个结点u和v称为e的端点。设边e=[u,v],若[u,v]是有序对,则称e是有向边有向边。其中结点u称为e的始点,结点v称为e的终点。+
西安电子科技大学 软件学院 无向边 有向边 §6.1.1 图的定义
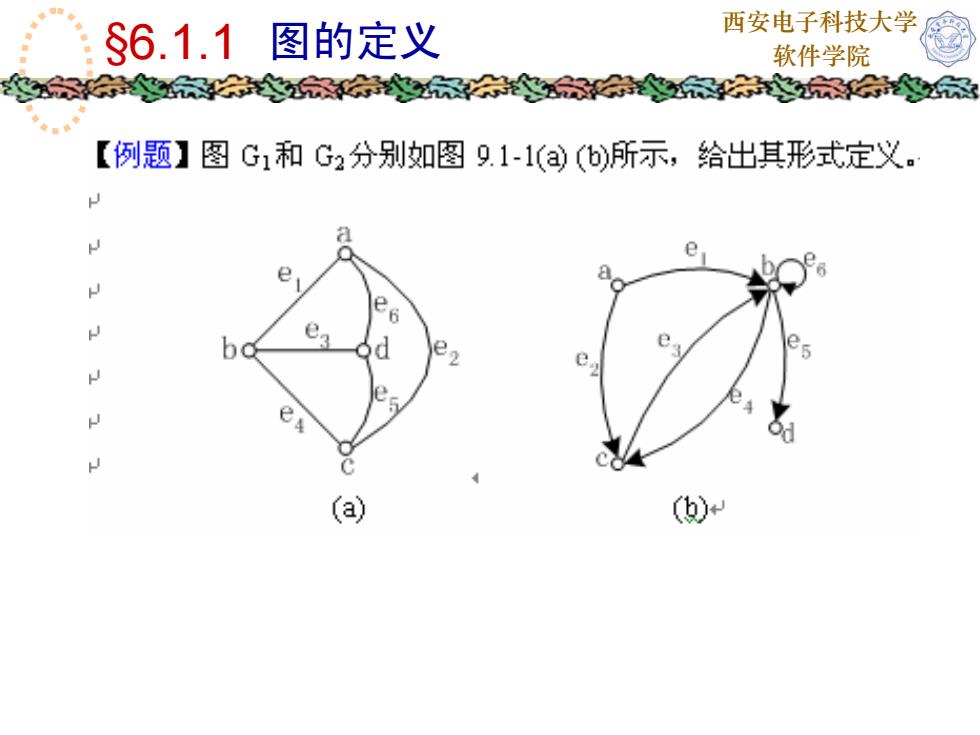
西安电子科技大学$6.1.1图的定义软件学院【例题】图G1和G2分别如图9.1-1(a)b)所示,给出其形式定义。YUJPO1oNodA(a)(b)+
西安电子科技大学 §6.1.1 图的定义 软件学院

西安电子科技大学$6.1.1图的定义软件学院解答:V(G1)=V(G2)-(a, b, c, d)+E(G1)-E(G2) -(e1, E2, e3, e4, es, e6) +Pg =(, , , , ,)+Pα =(>, >, >, >,>,>
西安电子科技大学 §6.1.1 图的定义 软件学院

西安电子科技大学$6.1.1[图的定义软件学院邻接点关联在同一条边上的两个结点相互邻接。关联于同一结点上的两条边相互邻接。邻接边仅关联一个结点的边称为自回路或环。自回路不与任何结点邻接的结点称为孤立结点。孤立结点设边er=[u,],若2=e且2是与ei不同的边,平行边则称ei与2是平行边。L
西安电子科技大学 软件学院 邻接点 邻接边 自回路 孤立结点 平行边 §6.1.1 图的定义

西安电子科技大学$6.1.2图的分类软件学院茶按边是否有方向可分为:(1)无向图:每条边都是无向边的图称为无向图。无向图的每条边关联的结点对是无序偶对。+(2)有向图:每条边都是有向边的图称为有向图。有向图的每条边关联的结点对是有序偶对,即ΦG:E(G)→V(G)×V(G)。 (3)混合图:图中一些边是有向边,而另外一些边是无向边,称该图为混合图
西安电子科技大学 §6.1.2 图的分类 软件学院

西安电子科技大学摩$6.1.2图的分类软件学院按边是否含平行边和自回路可分为:(1)多重图:含有平行边的图称为多重图。(2)线图:不含平行边的图称为线图。(3)简单图:不含自回路的线图称为简单图
西安电子科技大学 §6.1.2 图的分类 软件学院
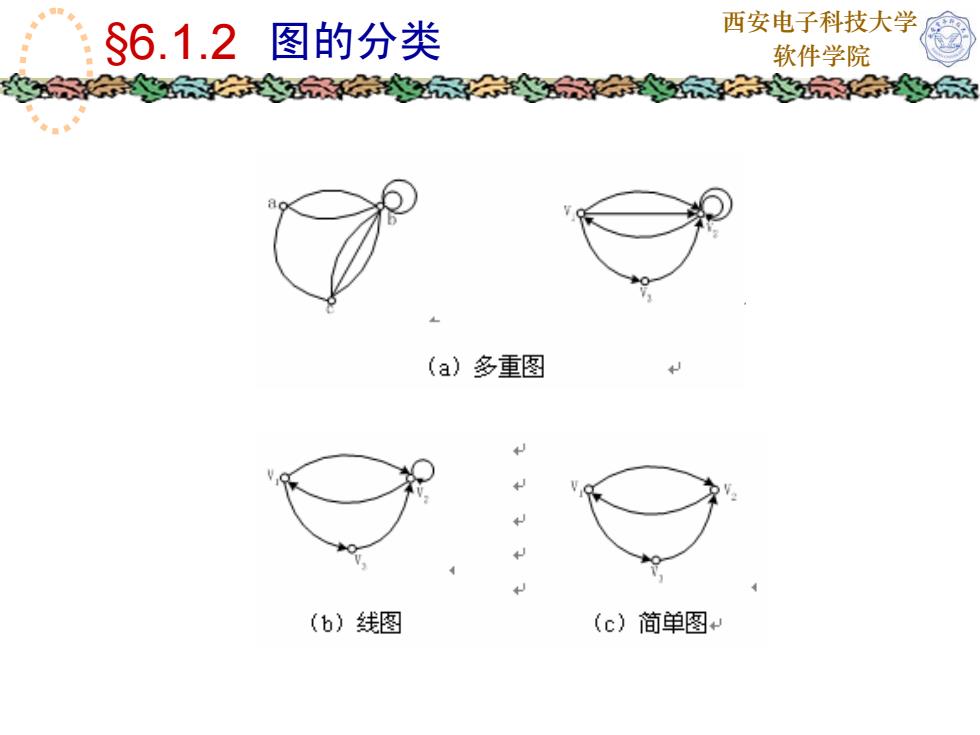
西安电子科技大学$6.1.2图的分类软件学院(a)多重图L(b)线图(c)简单图
西安电子科技大学 §6.1.2 图的分类 软件学院

西安电子科技大学$6.1.2图的分类软件学院家赋权图:赋权图G是一个四重组,其中是定义在结点集V到实数集R上的函数,h是定义在边集E到实数集R上的函数。(a)结点赋权图(b)边赋权图
西安电子科技大学 §6.1.2 图的分类 软件学院