
3.1.1直线的顿斜角和斜率(教学设计) 湖南省岳阳县第一中学邓超华 教学目标: 知识与技能 正确理解直线的倾斜角和斜率的概念 理解直线的倾斜角的唯一性 理解直线的斜率的存在性 斜率公式的推导过程,掌握过两点的直线的斜率公式 情感态度与价值观 ()通过直线的倾斜角概念的引入学习和直线倾斜角与斜率关系的揭示,培养学生观 察、探索能力,运用数学语言表达能力,数学交流与评价能力, ②)通过斜率概念的建立和斜率公式的推导,帮助学生进一步理解数形结合思想,培养 学生树立辩证统一的观点,培养学生形成严谨的科学态度和求简的数学精神。 重点与难点:直线的倾斜角、斜率的概念和公式。 教学用具:计算机 教学方法:启发、引导、讨论 教学过程: (一)直线的倾斜角的概念 我们知道,经过两点有且只有(确定)一条直线那么,经过一点P的直线1的位置能确定 吗?如图,过一点P可以作无数多条直线ab,c.易见,答案是否定的这些直线有什么联系呢
3.1.1 直线的倾斜角和斜率(教学设计) 湖南省岳阳县第一中学 邓超华 教学目标: 知识与技能 正确理解直线的倾斜角和斜率的概念. 理解直线的倾斜角的唯一性. 理解直线的斜率的存在性. 斜率公式的推导过程,掌握过两点的直线的斜率公式. 情感态度与价值观 (1) 通过直线的倾斜角概念的引入学习和直线倾斜角与斜率关系的揭示,培养学生观 察、探索能力,运用数学语言表达能力,数学交流与评价能力. (2) 通过斜率概念的建立和斜率公式的推导,帮助学生进一步理解数形结合思想,培养 学生树立辩证统一的观点,培养学生形成严谨的科学态度和求简的数学精神. 重点与难点: 直线的倾斜角、斜率的概念和公式. 教学用具:计算机 教学方法:启发、引导、讨论. 教学过程: (一)直线的倾斜角的概念 我们知道, 经过两点有且只有(确定)一条直线. 那么, 经过一点 P 的直线 l 的位置能确定 吗? 如图, 过一点 P 可以作无数多条直线 a,b,c, .易见,答案是否定的.这些直线有什么联系呢?

(1)它们都经过点卫.(2)它们的‘领斜程度'不同.怎样描述这种‘钡斜程度”的不同? 引入直线的倾斜角的概念: 当直线1与x轴相交时,取x轴作为基准,x轴正向与直线1向上方向之间所成的角ā叫 做直线1的倾斜角特别地,当直线1与x轴平行或重合时,规定α=0° 问:倾斜角a的取值范围是什么?0°≤a<180° 当直线1与x轴垂直时,a=90° 因为平面直角坐标系内的每一条直线都有确定的倾斜程度,引入直线的倾斜角之后,我 们就可以用倾斜角α来表示平面直角坐标系内的每一条直线的倾斜程度 如图,直线a∥b∥c,那么它们的倾斜角a相等吗?答案是肯定的.所以一个倾斜角a不 能确定一条直线确定平面直角坐标系内的一条直线位置的几何要素:一个点P和一个倾斜 角a
(1)它们都经过点 P. (2)它们的‘倾斜程度’不同. 怎样描述这种‘倾斜程度’的不同? 引入直线的倾斜角的概念: 当直线 l 与 x 轴相交时, 取 x 轴作为基准, x 轴正向与直线 l 向上方向之间所成的角α叫 做直线 l 的倾斜角.特别地,当直线 l 与 x 轴平行或重合时, 规定α= 0°. 问: 倾斜角α的取值范围是什么? 0°≤α<180°. 当直线 l 与 x 轴垂直时, α= 90°. 因为平面直角坐标系内的每一条直线都有确定的倾斜程度, 引入直线的倾斜角之后, 我 们就可以用倾斜角α来表示平面直角坐标系内的每一条直线的倾斜程度. 如图, 直线 a∥b∥c, 那么它们的倾斜角α相等吗? 答案是肯定的.所以一个倾斜角α不 能确定一条直线.确定平面直角坐标系内的一条直线位置的几何要素: 一个点 P 和一个倾斜 角α

(二)直线的斜率: 一条直线的倾斜角a(≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表 示也就是 k=tana ()当直线1与x轴平行或重合时,a=0°,k=tan0°=0: (2)当直线1与x轴垂直时,a=90°,k不存在 由此可知,一条直线1的倾斜角α一定存在,但是斜率k不一定存在 例如,a=45°时,k=tan45°=1; a=135°时,k=tan135°=tan(180°-45°)=-tan45°=-1. 学习了斜率之后,我们又可以用斜率来表示直线的倾斜程度 (三)直线的斜率公式: 给定两点P1(x1,y1),P2(2,y2x1≠x2,如何用两点的坐标来表示直线P1P2的斜率? 可用计算机作动画演示:直线P1P2的四种情况,并引导学生如何作辅助线 共同完成斜率公式的推导.(略) 斜率公式
(二)直线的斜率: 一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母 k 表 示,也就是 k = tanα ⑴当直线 l 与 x 轴平行或重合时, α=0°, k = tan0°=0; ⑵当直线 l 与 x 轴垂直时, α= 90°, k 不存在. 由此可知, 一条直线 l 的倾斜角α一定存在,但是斜率 k 不一定存在. 例如, α=45°时, k = tan45°= 1; α=135°时, k = tan135°= tan(180°- 45°) = - tan45°= - 1. 学习了斜率之后, 我们又可以用斜率来表示直线的倾斜程度. (三) 直线的斜率公式: 给定两点 P1(x1,y1),P2(x2,y2),x1≠x2,如何用两点的坐标来表示直线 P1P2的斜率? 可用计算机作动画演示: 直线 P1P2 的四种情况, 并引导学生如何作辅助线, 共同完成斜率公式的推导.(略) 斜率公式

k=y2-y1 82-X1 对于上面的斜率公式要注意下面四点: (1)当x1=x2时,公式右边无意义,直线的斜率不存在,倾斜角a=90°,直线与x轴 垂直 (2k与P1、P2的顺序无关,即y1,y2和x1,x2在公式中的前后次序可以同时交换,但分 子与分母不能交换; (3)斜率k可以不通过倾斜角而直接由直线上两点的坐标求得: (4)当y1与y2时,斜率k=0,直线的倾斜角a=0°,直线与x轴平行或重合 (⑤)求直线的倾斜角可以由直线上两点的坐标先求斜率而得到, (四)例愿: 例1已知A(3,2),B(-4),C(0-1),求直线AB,BC,CA的斜率,并判断它们的倾斜角是 钝角还是锐角.(用计算机作直线,图略) 分析:己知两点坐标,而且x≠x2,由斜率公式代入即可求得k的值 而当k=tana0时,倾斜角a是锐角: 而当k=tana-0时,领斜角a是0° 略解:直线AB的斜率k1=17>0,所以它的倾斜角a是锐角:
: 对于上面的斜率公式要注意下面四点: (1) 当 x1=x2 时,公式右边无意义,直线的斜率不存在,倾斜角α= 90°, 直线与 x 轴 垂直; (2)k 与 P1、P2 的顺序无关, 即 y1,y2 和 x1,x2 在公式中的前后次序可以同时交换, 但分 子与分母不能交换; (3)斜率 k 可以不通过倾斜角而直接由直线上两点的坐标求得; (4) 当 y1=y2 时, 斜率 k = 0, 直线的倾斜角α=0°,直线与 x 轴平行或重合. (5)求直线的倾斜角可以由直线上两点的坐标先求斜率而得到. (四)例题: 例 1 已知 A(3, 2), B(-4, 1), C(0, -1), 求直线 AB, BC, CA 的斜率, 并判断它们的倾斜角是 钝角还是锐角.(用计算机作直线, 图略) 分析: 已知两点坐标, 而且 x1≠x2, 由斜率公式代入即可求得 k 的值; 而当 k = tanα0 时, 倾斜角α是锐角; 而当 k = tanα=0 时, 倾斜角α是 0°. 略解: 直线 AB 的斜率 k1=1/7>0, 所以它的倾斜角α是锐角;

直线BC的斜率k2=-0.50,所以它的倾斜角a是锐角 例2在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2,及-3的直线a,b,c,1 分析:要画出经过原点的直线a只要再找出a上的另外一点M而M的坐标可以根 直线a的斜*确定;或者k=ana=l是特殊值,所以也可以以原点为角的顶点,x轴的正半轴为 角的一边,在x轴的上方作45°的角,再把所作的这一边反向延长成直线即可。 略解:设直线a上的另外一点M的坐标为xy),根据斜率公式有 1=y-0)/(x-0) 所以x=y 可令x=1,则y=1,于是点M的坐标为1,1).此时过原点和点 M1,l),可作直线a 同理,可作直线b,c,1.(用计算机作动画演示画直线过程) (五)练习:P911.2.3.4 (六)小结: ()直线的倾斜角和斜率的概念。 (2)直线的斜率公式 七)课后作业:P94习题311.3. (八)板书设计: S3.1.1. 1.直线倾斜角的概念 3.例1.练习1练习3
直线 BC 的斜率 k2=-0.50, 所以它的倾斜角α是锐角. 例 2 在平面直角坐标系中, 画出经过原点且斜率分别为 1, -1, 2, 及-3 的直线 a, b, c, l. 分析:要画出经过原点的直线 a, 只要再找出 a 上的另外一点 M. 而 M 的坐标可以根据 直线 a 的斜率确定; 或者 k=tanα=1 是特殊值,所以也可以以原点为角的顶点,x 轴的正半轴为 角的一边, 在 x 轴的上方作 45°的角, 再把所作的这一边反向延长成直线即可. 略解: 设直线 a 上的另外一点 M 的坐标为(x,y),根据斜率公式有 1=(y-0)/(x-0) 所以 x = y 可令 x = 1, 则 y = 1, 于是点 M 的坐标为(1,1).此时过原点和点 M(1,1), 可作直线 a. 同理, 可作直线 b, c, l.(用计算机作动画演示画直线过程) (五)练习: P91 1. 2. 3. 4. (六)小结: (1)直线的倾斜角和斜率的概念. (2) 直线的斜率公式. (七)课后作业: P94 习题 3.1 1. 3. (八)板书设计: §3.1.1. 1.直线倾斜角的概念 3.例 1. 练习 1 练习 3

2.直线的斜率 4例2.练习2练习4 3.2.1直线的点斜式方程(教学设计) 湖南省岳阳县第一中学邓超华 一、教学目标 1、知识与技能 (1)理解直线方程的点斜式、斜截式的形式特点和适用范围: (2)能正确利用直线的点斜式、斜截式公式求直线方程。 (3)体会直线的斜截式方程与一次函数的关系」 2、过程与方法 在己知直角坐标系内确定一条直线的几何要素一一直线上的一点和直线的倾斜角的基 础上,通过师生探讨,得出直线的点斜式方程:学生通过对比理解“截距”与“距离”的 区别。 3、情态与价值观 通过让学生体会直线的斜截式方程与一次函数的关系,进一步培养学生数形结合的思 想,渗透数学中普遍存在相互联系、相互转化等观点,使学生能用联系的观点看问题。 二、教学重点、难点: (1)重点:直线的点斜式方程和斜截式方程 (2)难点:直线的点斜式方程和斜截式方程的应用。 三、敦学设想 设计意图 师生活动 1、在直线坐标系内确定一条直 使学生在己右 饮后物伍指 线,应知道哪些条 知识和经验的基 出,直线的方程,就是直线上任 础上,探索新 知。 一点的坐标(x,y)满足的关系式。 2、直线经过点(氏),且塘的能,自 培养学生自主 学生根据斜率公式,可以得到
2. 直线的斜率 4.例 2. 练习 2 练习 4 3.2.1 直线的点斜式方程(教学设计) 湖南省岳阳县第一中学 邓超华 一、教学目标 1、知识与技能 (1)理解直线方程的点斜式、斜截式的形式特点和适用范围; (2)能正确利用直线的点斜式、斜截式公式求直线方程。 (3)体会直线的斜截式方程与一次函数的关系. 2、过程与方法 在已知直角坐标系内确定一条直线的几何要素——直线上的一点和直线的倾斜角的基 础上,通过师生探讨,得出直线的点斜式方程;学生通过对比理解“截距”与“距离”的 区别。 3、情态与价值观 通过让学生体会直线的斜截式方程与一次函数的关系,进一步培养学生数形结合的思 想,渗透数学中普遍存在相互联系、相互转化等观点,使学生能用联系的观点看问题。 二、教学重点、难点: (1)重点:直线的点斜式方程和斜截式方程。 (2)难点:直线的点斜式方程和斜截式方程的应用。 三、教学设想 问 题 设计意图 师生活动 1、在直线坐标系内确定一条直 线,应知道哪些条件? 使学生在已有 知识和经验的基 础 上 , 探 索 新 知。 学生回顾,并回答。然后教师指 出,直线的方程,就是直线上任意 一点的坐标 满足的关系式。 2、直线 经过点 ,且 培养学生自主 探索的能力,并 学生根据斜率公式,可以得到
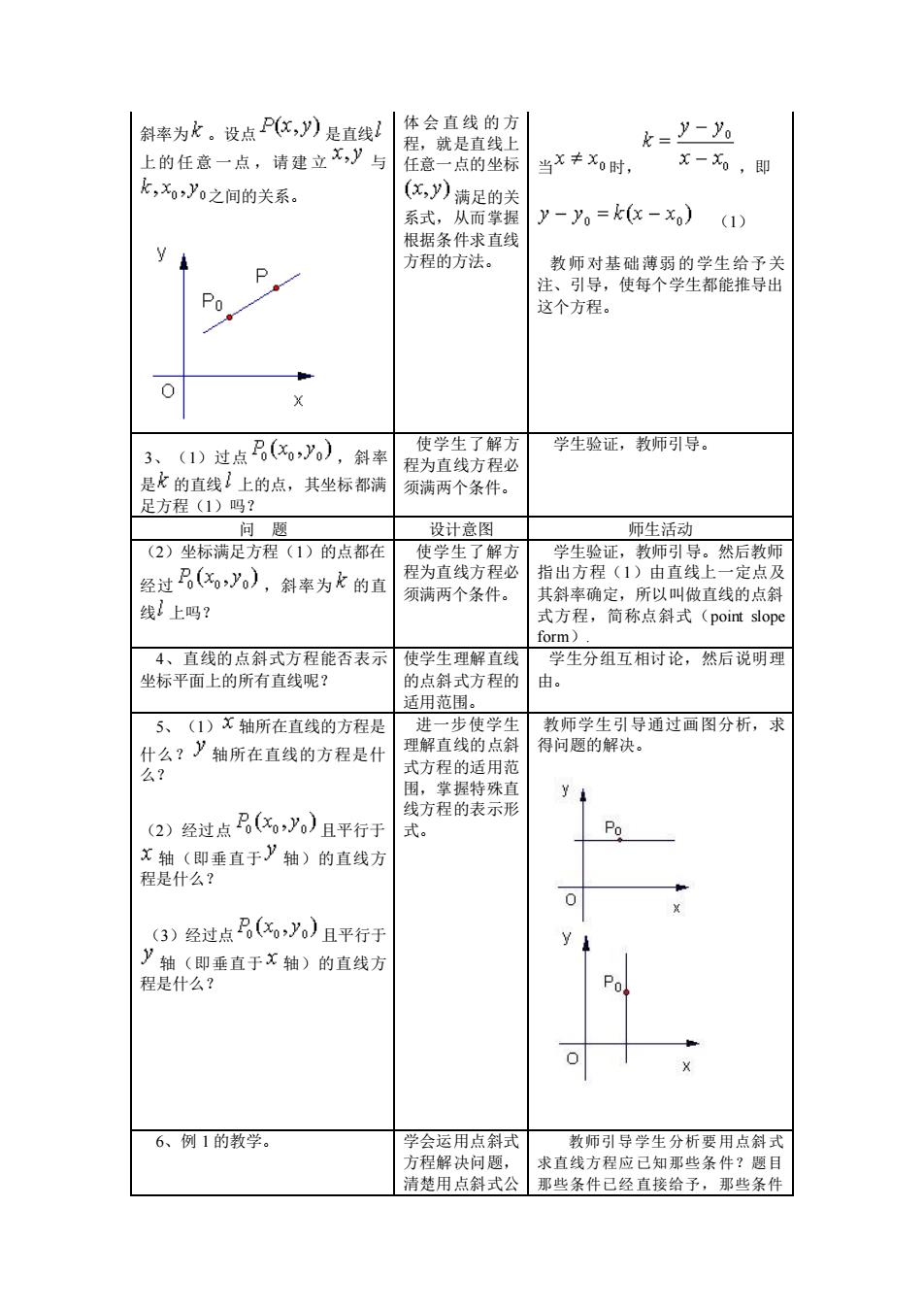
斜率为北。设点P化,》是直线体会直线的方 就是直线 =y-为 上的任意一点,请建立x,》与 任意 一点的坐材 当x≠x0时, x一x,即 k,y0之间的关系 (x,y)满足的》 系式, y-y。=k-x)1) y P 教师对基础薄弱的学生给予关 Po 这个方程 使每个学生都能推导出 3、(1)过点(x》),斜率 使学生了解方 学生验证,教师引导。 程为直线方程必 是化的直线!上的点,其坐标都满 须满两个条件。 足方程(1)吗 设计意图 师生活过 (2)坐标满足方程(1)的点都 经过(),斜率为k的直 指先 :然后 须满两个条件。 剑率确定 所以叫做直线的点斜 线上吗? 式方程 简称点斜式(po slon form) 4、直线的点斜式方程能否表示使学生理解直线 学生分组互相讨论,然后说明理 坐标平面上的所有直线呢? 的点斜式方程的 由。 语用节围。 5、(1)x轴所在直线的方程是 进一步使学生 救师学生引导通过画图分析,求 什么?y轴所在直线的方程是什 理解直线的点斜 得问颗的解快。 式方程的适用范 围,掌握特殊直 线方程的表示形 (2)经过点(,g)且平行于 式。 x轴(即垂直于y轴)的直线方 得是什么? (3)经过点(y)且平行于 y 6、例1的教学。 学会运用点斜式 教师引导学生分析要用点斜式 清楚用点斜式公些条件巴经直接给,事些条件 父直线 程
斜率为 。设点 是直线 上的任意 一点 ,请建 立 与 之间的关系。 体 会 直 线 的 方 程,就是直线上 任意一点的坐标 满足的关 系式,从而掌握 根据条件求直线 方程的方法。 当 时, ,即 (1) 教师对基础薄弱的学生给予关 注、引导,使每个学生都能推导出 这个方程。 3、(1)过点 ,斜率 是 的直线 上的点,其坐标都满 足方程(1)吗? 使学生了解方 程为直线方程必 须满两个条件。 学生验证,教师引导。 问 题 设计意图 师生活动 (2)坐标满足方程(1)的点都在 经过 ,斜率为 的直 线 上吗? 使学生了解方 程为直线方程必 须满两个条件。 学生验证,教师引导。然后教师 指出方程(1)由直线上一定点及 其斜率确定,所以叫做直线的点斜 式方程,简称点斜式(point slope form). 4、直线的点斜式方程能否表示 坐标平面上的所有直线呢? 使学生理解直线 的点斜式方程的 适用范围。 学生分组互相讨论,然后说明理 由。 5、(1) 轴所在直线的方程是 什么? 轴所在直线的方程是什 么? (2)经过点 且平行于 轴(即垂直于 轴)的直线方 程是什么? (3)经过点 且平行于 轴(即垂直于 轴)的直线方 程是什么? 进一步使学生 理解直线的点斜 式方程的适用范 围,掌握特殊直 线方程的表示形 式。 教师学生引导通过画图分析,求 得问题的解决。 6、例 1 的教学。 学会运用点斜式 方程解决问题, 清楚用点斜式公 教师引导学生分析要用点斜式 求直线方程应已知那些条件?题目 那些条件已经直接给予,那些条件
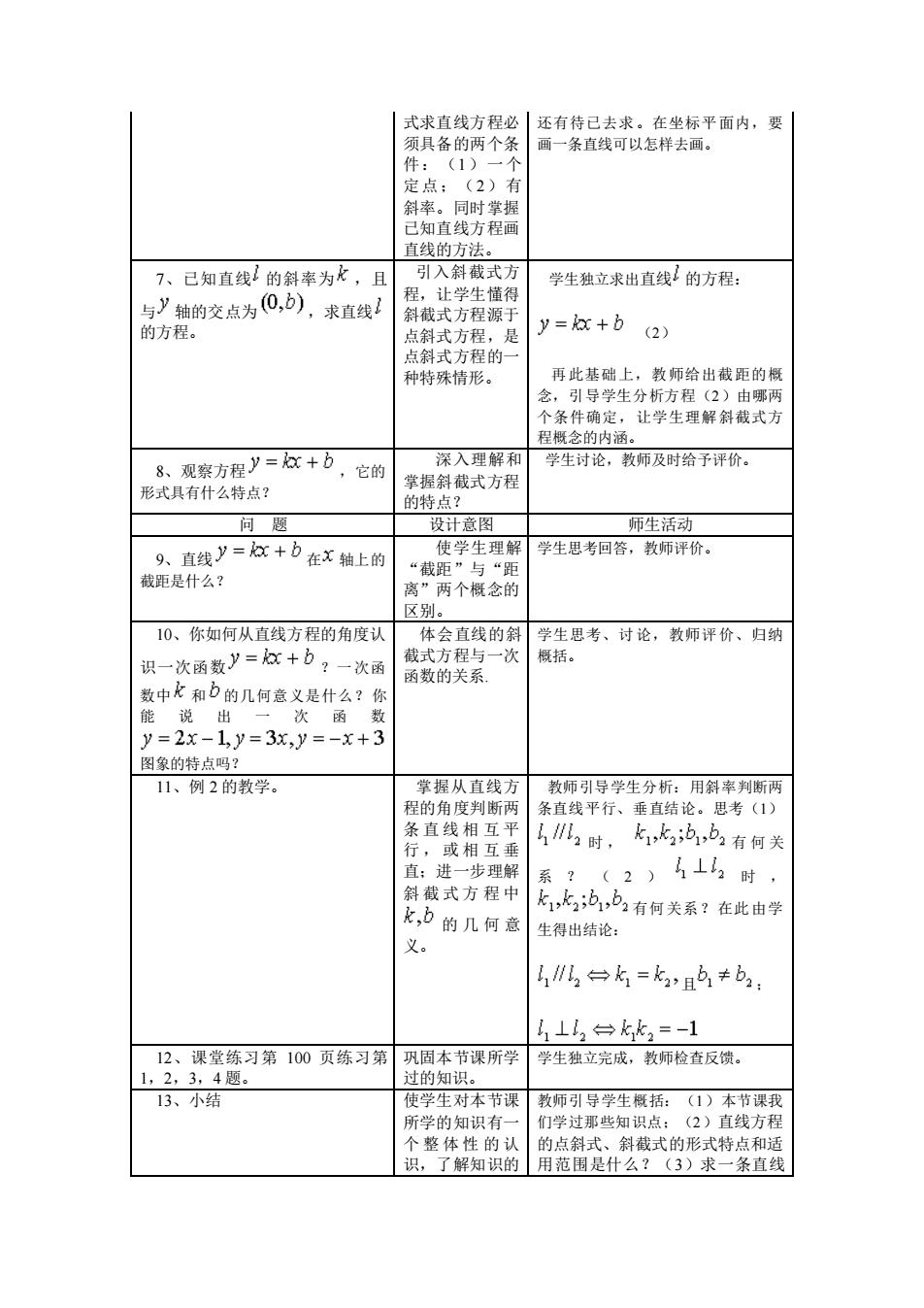
式求直线方程必|还有待已去求。在坐标平面内,要 须具备的两个条 画一条直线可以怎样去画。 (1) (2) 有 直线的 7、已知直线的斜*为北,且 引入金 学生独立求出直线!的方程: 与y轴的交点为0,),求直线 的方程。 点斜式方程,是 y=x+b(2) 占斜式方程的 种结殊情形。 再此基础上 教师给出截距的橱 学生 件确定 学生理解斜数大 8、观察方程y=+b,它的 入理和 学生讨论,教师及时给予评价 形式具有什 久特占? 掌斜截式方程 的装占2 沿斗普网 压出活动 9、直线y=+b在x轴上的 审学牛理解 学生思考回答,教师评价 4与“阳 雄距是什久? 离”两个概念的 风别。 10、你如何从直线方程的角度认 体会直线的斜学生思老、讨论,数师评价、归纳 识一次函数》=众+b,一次函 截式方程与一次 概括。 函数的关系, 图象的特点吗: 11、例2的教学。 掌握从直线方 教师引导学生分析:用斜率判断两 程的角度判断两 条直线平行、垂直结论。思考(1) 12时, kk2;b,b2有何关 系? 2)1时 k,k2;b,b2有何关系?在此由学 生得出结论: 义。 {,台k=k的+b. 11112台kk2=-1 12、课堂练习第100页练习第巩固本节课所学 学生独立完成,教师检查反馈。 1.2.3.4期 过的知识。 13、小结 使学生对本节课 教师引导学生概括:(1)本节课我 所学的知识有 们学过那些知识点:(2)直线方程 个整体性的认 的点斜式、斜截式的形式特点和适 识,了解知识的用范围是什么?(3)求一条直线
式求直线方程必 须具备的两个条 件:(1)一个 定点;(2)有 斜率。同时掌握 已知直线方程画 直线的方法。 还有待已去求。在坐标平面内,要 画一条直线可以怎样去画。 7、已知直线 的斜率为 ,且 与 轴的交点为 ,求直线 的方程。 引入斜截式方 程,让学生懂得 斜截式方程源于 点斜式方程,是 点斜式方程的一 种特殊情形。 学生独立求出直线 的方程: (2) 再此基础上,教师给出截距的概 念,引导学生分析方程(2)由哪两 个条件确定,让学生理解斜截式方 程概念的内涵。 8、观察方程 ,它的 形式具有什么特点? 深入理解和 掌握斜截式方程 的特点? 学生讨论,教师及时给予评价。 问 题 设计意图 师生活动 9、直线 在 轴上的 截距是什么? 使学生理解 “截距”与“距 离”两个概念的 区别。 学生思考回答,教师评价。 10、你如何从直线方程的角度认 识一次函数 ?一次函 数中 和 的几何意义是什么?你 能说出一次函数 图象的特点吗? 体会直线的斜 截式方程与一次 函数的关系. 学生思考、讨论,教师评价、归纳 概括。 11、例 2 的教学。 掌握从直线方 程的角度判断两 条 直 线 相 互 平 行 , 或 相 互 垂 直;进一步理解 斜 截 式 方 程 中 的几何意 义。 教师引导学生分析:用斜率判断两 条直线平行、垂直结论。思考(1) 时 , 有何关 系?( 2 ) 时 , 有何关系?在此由学 生得出结论: 且 ; 12、课堂练习第 100 页练习第 1,2,3,4 题。 巩固本节课所学 过的知识。 学生独立完成,教师检查反馈。 13、小结 使学生对本节课 所学的知识有一 个 整 体 性 的 认 识,了解知识的 教师引导学生概括:(1)本节课我 们学过那些知识点;(2)直线方程 的点斜式、斜截式的形式特点和适 用范围是什么?(3)求一条直线

来龙去脉。 的方程,要知道多少个条件? 14、布置作业:第106页第1题巩固深化 的0D、2、《s)和第g 学生课后独立完成。 3.2.3直线的一般式方程(教学设计 湖南省岳阳县第一中学邓超华 一、教学目标 1、知识与技能 (1)明确直线方程一般式的形式特征: (2)会把直线方程的一般式化为斜截式,进而求斜率和截距: (3)会把直线方程的点斜式、两点式化为一般式。 2、过程与方法 学会用分类讨论的思想方法解决问题。 3、情态与价值观 (1)认识事物之间的普遍联系与相互转化: (2)用联系的观点看问题。 二、敦学重点、难点: 1、重点:直线方程的一般式。 2、难点:对直线方程一般式的理解与应用。 三、散学设想 司题 设计意图 师生活动 1. (1)平面直角坐标系中的每使学生理解直 教师引导学生用分类讨论的方法思考 条直线都可以用一个关于 线和二元一次 探究问题(1),即直线存在斜率和直 x,》的二元一次方程表示吗名 方程的关系。 线不存在斜率时求出的直线方程是否 都为二元一次方程。对于问题(2)
来龙去脉。 的方程,要知道多少个条件? 14、布置作业:第 106 页第 1 题 的(1)、(2)、(3)和第 3、5 题 巩固深化 学生课后独立完成。 3.2.3 直线的一般式方程(教学设计) 湖南省岳阳县第一中学 邓超华 一、教学目标 1、知识与技能 (1)明确直线方程一般式的形式特征; (2)会把直线方程的一般式化为斜截式,进而求斜率和截距; (3)会把直线方程的点斜式、两点式化为一般式。 2、过程与方法 学会用分类讨论的思想方法解决问题。 3、情态与价值观 (1)认识事物之间的普遍联系与相互转化; (2)用联系的观点看问题。 二、教学重点、难点: 1、重点:直线方程的一般式。 2、难点:对直线方程一般式的理解与应用。 三、教学设想 问 题 设计意图 师生活动 1、(1)平面直角坐标系中的每 一 条 直 线都 可以 用 一个 关 于 的二元一次方程表示吗? 使学生理解直 线和二元一次 方程的关系。 教师引导学生用分类讨论的方法思考 探究问题(1),即直线存在斜率和直 线不存在斜率时求出的直线方程是否 都为二元一次方程。对于问题(2)

(2)每一个关于x,y的二元 教师引导学生理解要判断某一个方程 次方程A收+y+C=0 是否表示一条直线,只需看这个方程 是否可以转化为直线方程的某种 同时为0)都表示 条直线吗? 式。为此要对B分类讨论,即当 B≠0时和当B0时两种情形进行变 形。然后由学生去变形判断,得出结 论 关于x,》的二元一次方程,它都表 示一条直线。 教师概括指出:由于任何一条直线都 可以用一个关于x,y的二元 方程 表示:同时,任何一个关于x,》的 元一次方程都表示一条直线。 我们把关于关于,y的二元一次) 程Ax+砂+C=0A,B不同时 为0)叫做直线的一般式方程,简称 直纱方程的一船式与其他 学生诵过过出、过 发现直线方程 种形式的直线方程相比,它有什 使学牛理解 我方积的 一般式与其他形式的直线方程的 么优占? 式的与其他形 个不同占是. 问题 设计意图 师生活动 式的不同点。 直线的一般式方程能够表示平面上的 所有直线,而点斜式、斜截式、两点 式方程,都不能表示与x轴垂直的直 3、在方程Ar+y+C=0 使学生理解 次方程的 教师引导学生回顾前面所学过的与 中,A,B,C为何值时,方程 轴平行和重合、与'轴平行和重合的 表示的直线 系数和常数可 对直线的位置 直线方程的形式。然后由学生自主探 索得到问题的答案。 的影响。 (1)平行干x轴:(2)平行 于y轴:(3)与x轴重合 (4)与y重合. 4、例5的教学 使学牛体合把 学生独立完成。然后教师检查、评 直线方程的点 价、反馈。指出:对于直线方程的 已知直线经过点A(6,4), 斜式转化为 般式, 一般作如下约定:一般按含x 4 般式,把握 项、含项、常数项顺序排列:x项 线方程一般式 斜率为3,求直线的点斜式 的特点。 的系数为正:文,的系数和常数项 和一般式方程。 般不出现分数:无特加要时,求直 线方程的结果写成一般式。 5、例6的教学 使学生体会直 先由学生思考解答,并让一个学生上 线方程的一般 黑板板书。然后教师引导学生归纳出 把直线的一般式方程 式化为斜截 由直线方程的一般式,求直线的斜率 式,和己知直 和截距的方法:把一骰式转化为截
(2)每一个关于 的二元一 次方程 (A,B 不同时为 0)都表示一 条直线吗? 教师引导学生理解要判断某一个方程 是否表示一条直线,只需看这个方程 是否可以转化为直线方程的某种形 式。为此 要对 B 分类 讨论, 即当 时和当 B=0 时两种情形进行变 形。然后由学生去变形判断,得出结 论: 关于 的二元一次方程,它都表 示一条直线。 教师概括指出:由于任何一条直线都 可以用一个关于 的二元一次方程 表示;同时,任何一个关于 的二 元一次方程都表示一条直线。 我们把关于关于 的二元一次方 程 (A,B 不同时 为 0)叫做直线的一般式方程,简称一 般式(general form). 2、直线方程的一般式与其他几 种形式的直线方程相比,它有什 么优点? 使学生理解直 线方程的一般 式的与其他形 学生通过对比、讨论,发现直线方程 的一般式与其他形式的直线方程的一 个不同点是: 问 题 设计意图 师生活动 式的不同点。 直线的一般式方程能够表示平面上的 所有直线,而点斜式、斜截式、两点 式方程,都不能表示与 轴垂直的直 线。 3、在方程 中,A,B,C 为何值时,方程 表示的直线 (1)平行于 轴;(2)平行 于 轴;(3)与 轴重合; (4)与 重合。 使学生理解二 元一次方程的 系数和常数项 对直线的位置 的影响。 教师引导学生回顾前面所学过的与 轴平行和重合、与 轴平行和重合的 直线方程的形式。然后由学生自主探 索得到问题的答案。 4、例 5 的教学 已知直线经过点 A(6,-4), 斜率为 ,求直线的点斜式 和一般式方程。 使学生体会把 直线方程的点 斜式转化为一 般式,把握直 线方程一般式 的特点。 学生独立完成。然后教师检查、评 价、反馈。指出:对于直线方程的一 般式,一般作如下约定:一般按含 项、含 项、常数项顺序排列; 项 的系数为正; , 的系数和常数项 一般不出现分数;无特加要时,求直 线方程的结果写成一般式。 5、例 6 的教学 把直线 的 一 般 式 方 程 使学生体会直 线方程的一般 式化为斜截 式,和已知直 先由学生思考解答,并让一个学生上 黑板板书。然后教师引导学生归纳出 由直线方程的一般式,求直线的斜率 和截距的方法:把一般式转化为斜截