
西安电子科技大学离散数学软件学院第二篇集合论第3章集合与关系第13课时23.1集合及其运算第14课时一3.2二元关系第15课时3.3集合上的二元关系及其特性第16课时大3.4关系的闭包运算第17-课18时3.5等价关系第20课时3.6序关系(2)
西安电子科技大学 离散数学 软件学院 第二篇 集合论 第13课时 3.1 集合及其运算 第3章 集合与关系 3.4 关系的闭包运算 3.2 二元关系 3.5 等价关系 第14课时 第16课时 第17-课18时 第15课时 3.3 集合上的二元关系及其特性 第20课时 3.6 序关系(2)

西安电子科技大学$3.6.3偏序集合中的特殊元素软件学院设是偏序集合,B二A。aEA,若对于B中的任意元素b,均有b<a,称a上界为B的上界。比B中元素均“大”的元素称为B的上界。aEA,若对于B中的任意元素b,均有ab,称a下界为B的下界。比B中元素均“小”的元素称为B的下界
西安电子科技大学 软件学院 上界 下界 §3.6.3 偏序集合中的特殊元素 设是偏序集合,B⊆A。 比B中元素均“大”的元素称为B的上界。 比B中元素均“小”的元素称为B的下界

西安电子科技大学$3.6.3偏序集合中的特殊元素软件学院家家设是偏序集合,B二A。a为B的上界,若对B的任意上界a,均有a<a,最小上界称a为B的最小上界(上确界),记为lub。B的所有上界中的最小元为其最小上界,a为B的下界,若对B的任意下界a,均有a'<a,最大下界称a为B的最大下界(下确界),记为glb。B的所有下界中的最大元为其最大下界
西安电子科技大学 软件学院 最小上界 最大下界 B的所有下界中的最大元为其最大下界。 §3.6.3 偏序集合中的特殊元素 设是偏序集合,B⊆A。 B的所有上界中的最小元为其最小上界
西安电子科技大学$3.6.3偏序集合中的特殊元素软件学院家【例题】A={(1,2,,12},≤为A上的整除关系,的哈斯图如图所示,求B=2,4,6),C=(4,6,9),D=(1,2,5,10)的特殊元素。解答:B、C、D中的特殊元素如表所示。上下最小极小极大最大最小元最大元界界上界元元下界22121,2122(2, 4, 6)4,6X1XXX1X(4, 6, 9)4, 6,94,6,9101101010111(1, 2, 5, 10)
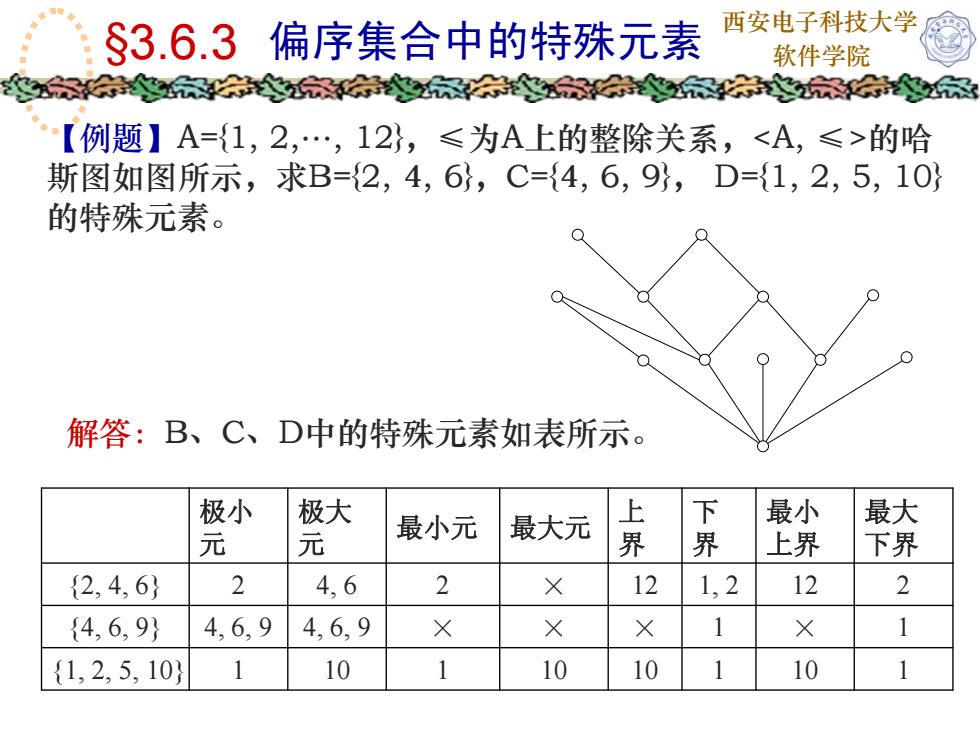
西安电子科技大学 §3.6.3 偏序集合中的特殊元素 软件学院 【例题】A={1, 2,., 12},≤为A上的整除关系,的哈 斯图如图所示,求B={2, 4, 6},C={4, 6, 9}, D={1, 2, 5, 10} 的特殊元素。 解答:B、C、D中的特殊元素如表所示。 极小 元 极大 元 最小元 最大元 上 界 下 界 最小 上界 最大 下界 {2, 4, 6} 2 4, 6 2 × 12 1, 2 12 2 {4, 6, 9} 4, 6, 9 4, 6, 9 × × × 1 × 1 {1, 2, 5, 10} 1 10 1 10 10 1 10 1

西安电子科技大学S3.6.3偏序集合中的特殊元素软件学院『定理』设是偏序集合,BA。(a)若b是B的最大元,则b是B的极大元;(b)若b是B的最大元,则b是B的最小上界:(c)bEB,若b是B的上界,当且仅当b是B是的最小上界:(d)若b是B的最小元,则b是B的极小元;(e)若b是B的最小元,则b是B的最大下界;(f)bEB,若b是B的下界,当且仅当b是B的最大下界
西安电子科技大学 §3.6.3 偏序集合中的特殊元素 软件学院 『定理』设是偏序集合,B ⊆A。 (a)若b是B的最大元,则b是B的极大元; (b)若b是B的最大元,则b是B的最小上界; (c)b∈B,若b是B的上界,当且仅当b是B是的最小上界; (d)若b是B的最小元,则b是B的极小元; (e)若b是B的最小元,则b是B的最大下界; (f)b∈B,若b是B的下界,当且仅当b是B的最大下界

西安电子科技大学$3.6.4线序集合软件学院在偏序集合中,如果A中的任意两个元素线序都是可比的,那么叫做线序集合或链。在一个偏序集合中如果任意两个元素都是可比的,称该偏序集合为线序集合,线序集合的哈斯图是一根链
西安电子科技大学 线序集合 软件学院 线序 §3.6.4 在偏序集合中,如果A中的任意两个元素 都是可比的,那么≼叫做A上的线序或全序, 叫做线序集合或链。 在一个偏序集合中如果任意两个元素都是 可比的,称该偏序集合为线序集合,线序 集合的哈斯图是一根链

西安电子科技大学$3.6.4线序集合软件学院家教家教家【例题】判断以下是否是线序集合(a),其中N是自然数集合(b) A=(a, b, c), ×(c) v
西安电子科技大学 §3.6.4 线序集合 软件学院 【例题】判断以下是否是线序集合。 (a),其中N是自然数集合 (b) A={a, b, c}, (c) × √ √

西安电子科技大学$3.6.5格软件学院格设是一个偏序集合,如果集合L中的任意两个元素都有最小上界和最大下界,则称为格。任意两个元素都有最小上界和最大小界的偏序集合称为格
西安电子科技大学 软件学院 格 §3.6.5 格 设是一个偏序集合,如果集合L中的任 意两个元素都有最小上界和最大下界,则称为格。 任意两个元素都有最小上界和最大小界的 偏序集合称为格

西安电子科技大学$3.6.5格软件学院【例题】判断图8.1-1所示各哈斯图表示的偏序集合是否是格?OnXX(a)(b)(c)O.(d)(e)(f)(h)(g)V/VV
西安电子科技大学 §3.6.5 格 软件学院 【例题】判断图8.1-1所示各哈斯图表示的偏序集合是否是格? × √ √ √ √ √ × ×

西安电子科技大学$3.6.5格软件学院【例题】设I是正整数集合,定义I+上的二元关系“「”,任取a,bEIt,a/b当且仅当a能整除b。证明:是一个格。证明:I+上的二元关系是自反、反对称和传递的,因此I,>是一个偏序集合。任取a,beIt,a与b在偏序集合中的最小上界是其最小公倍数:lub(a,b) elt.任取a,b=It,a与b在偏序集合中的最大下界是其最大公约数:glb(a,b)elt.故是一个格
西安电子科技大学 §3.6.5 格 软件学院 【例题】设I+是正整数集合,定义I+上的二元关系“|”,任取 a,b ∈I+,a|b当且仅当a能整除b。证明:是一个格