
西安电子科技大学离散数学软件学院第一篇数理逻辑第2章谓词逻辑V第7课时1.1谓词和量词第8课时1.2谓词公式→第9课时1.3谓词公式的翻译41第10课时1.4谓词演算的永真公式第11课时1.5谓词演算的四个推理规则第12课时1.6谓词逻辑推理及应用二
西安电子科技大学 离散数学 软件学院 第一篇 数理逻辑 第7课时 1.1 谓词和量词 第2章 谓词逻辑 1.4 谓词演算的永真公式 1.2 谓词公式 1.5 谓词演算的四个推理规则 第8课时 第10课时 第11课时 第9课时 1.3 谓词公式的翻译 第12课时 1.6 谓词逻辑推理及应用

西安电子科技大学$2.6.1谓词逻辑推理证明方法软件学院家家家【例题】符号化以下语句,并推证结论的有效性,“每个人都是要死的,苏格拉底是人,所以苏格拉底是要死的。解答:设论域为全总个体域,M(x):x是人,D(x):x是要死的,a:苏格拉底。现要证明以下永真式:(x)(M(x)-D(x) AM(a)→D(a)P(1) M(a)P(2) (Vx(M(x)-D(x)(3) M(a)D(a)T (2) US(4) D(a)T(1)(3)I
西安电子科技大学 §2.6.1 谓词逻辑推理证明方法 软件学院
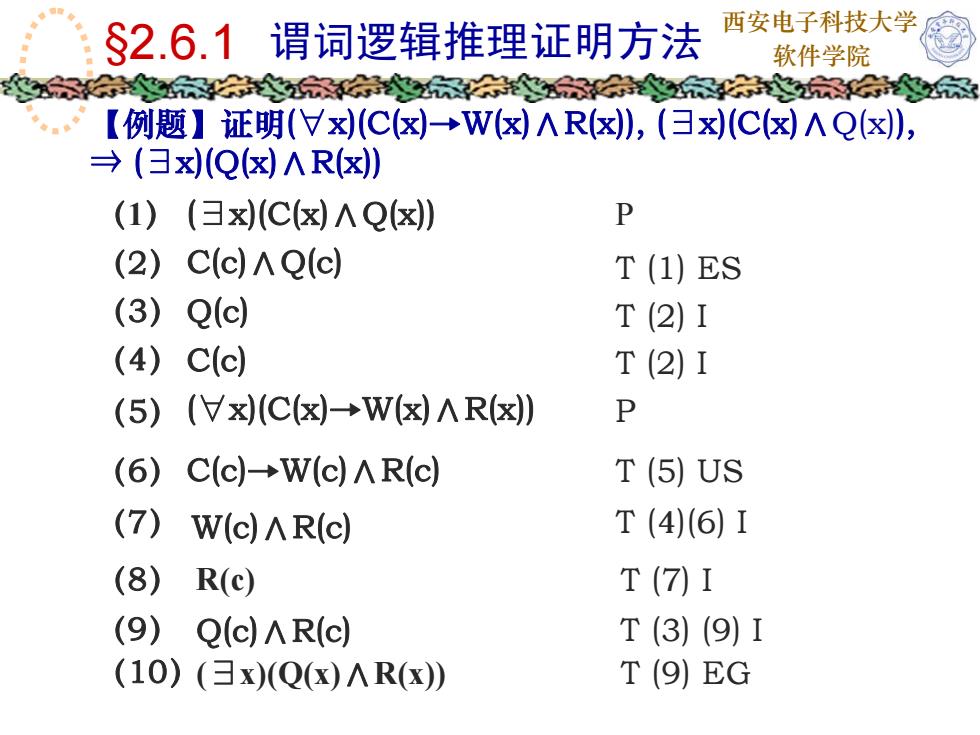
西安电子科技大学$2.6.1谓词逻辑推理证明方法软件学院【例题 证明(x)(C(×)→W(×) ΛR(x)), (日x)(C(x) ΛQ()), (日x)(Q(≤) ^R(x))P(1) (日x)(C(×) ^Q(×)(2)C(c) Λ Q(c)T (1) ES(3)Q(c)T (2) I(4)C(c)T (2) IP(5)(V x)(C(×)-→W(×) ^R(×)(6)C(c)-W(c) ^R(c)T (5) US(7)T (4)(6) IW(c) ^R(c)(8)T (7) IR(c)(9)T (3) (9) IQ(c) ^R(c)(10) (日x)(Q(x) ^R(x)T (9) EG
西安电子科技大学 §2.6.1 谓词逻辑推理证明方法 软件学院 【例题】证明( ∀x)(C(x)→W(x)∧R(x)), ( ∃x)(C(x)∧Q(x)), ⇒ ( ∃x)(Q(x)∧R(x)) ( 1 ) ( ∃x)(C(x)∧Q(x)) P (2) T (1) ES (5) P (6) T (5) US (7) W(c)∧R(c) T (4)(6) I (8) R(c) T (7) I (3) T (2) I (4) T (2) I C(c)∧Q(c) Q(c) C(c) ( ∀x)(C(x)→W(x)∧R(x)) C(c)→W(c)∧R(c) (9) Q(c)∧R(c) T (3) (9) I (10) ( ∃x)(Q(x) ∧R(x)) T (9) EG

西安电子科技大学$2.6.1谓词逻辑推理证明方法软件学院茶【例题】证明(Vx)(P(×)VQ(×))=(Vx)P() V (日x)Q(x)方法一、反证法(1)-((Vx)P(x) V(三x)Q(x)P(假设前提)(2) -(Vx) P(x) ^ -(三x)Q(x)T (1) E(3)-(Vx) P(x)T (2) I(4)(x)-P(x)T (3) E(5)- P(a)T (4) ESP(6)(Vx)(P(x) VQ(x))(7)T (6) USP(a) V Q(a)(8)Q(a)T (5)(7) I
西安电子科技大学 §2.6.1 谓词逻辑推理证明方法 软件学院 【例题】证明 ( ∀x)(P(x)∨Q(x)) ⇒ ( ∀x)P(x)∨( ∃x)Q(x) 方法一、反证法 ( 1 ) ¬( ( ∀x)P(x) ∨ ( ∃x)Q(x)) P(假设前提 ) (2) ¬ ( ∀x) P(x) ∧ ¬ ( ∃x)Q(x) T (1) E (5) ¬ P(a) T (4) ES (6) ( ∀x)(P(x) ∨Q(x)) P (7) P(a) ∨Q(a)) T (6) US (8) Q(a)) T (5)(7) I (3) ¬ ( ∀x) P(x) T (2) I (4) ( ∃x) ¬P(x) T (3) E

西安电子科技大学$2.6.1谓词逻辑推理证明方法软件学院-【例题)证明(Vx)(P(≤) VQ(×)=(Vx)P(×)V (x)Q(x)方法一、反证法(9) (日x)Q(β)T (8) EGT (2) I(10 -(3x)Q(x) (11 (3x)Q(x)△-(x)Q(x)矛盾)
西安电子科技大学 §2.6.1 谓词逻辑推理证明方法 软件学院 【例题】证明 ( ∀x)(P(x)∨Q(x)) ⇒ ( ∀x)P(x)∨( ∃x)Q(x) 方法一、反证法 (9) ( ∃x)Q(x) T (8) EG (10 ) ¬ ( ∃x)Q(x) T (2) I (11 ) ( ∃x)Q(x) ∧ ¬ ( ∃x)Q(x) 矛盾

西安电子科技大学$2.6.1谓词逻辑推理证明方法软件学院【例题】证明(Vx)(P(×) VQ(×)=(Vx)P(×) V (日x)Q(x方法一、CP规则法将原式变形为:(日x)(P(x) VQ(x)→(Vx)P(x)→(日x)Q(x)(1) -(Vx)P(x)P(附加前提)(2)T (1) E(=x)-P(x)(3)- P(a)T (2) ESP(4)(Vx)(P(x) VQ(x)(5)T (4) USP(a) VQ(a)(6)Q(a)T (3)(5) I(7)(日x)Q(β)T (6) EG
西安电子科技大学 §2.6.1 谓词逻辑推理证明方法 软件学院 【例题】证明 ( ∀x)(P(x)∨Q(x)) ⇒ ( ∀x)P(x)∨( ∃x)Q(x) 方法一、CP规则法 将原式变形为: ( ∃x)(P(x) ∨Q(x)) ⇒ ¬ ( ∀x)P(x) → ( ∃x)Q(x) ( 1 ) ¬ ( ∀x)P(x) P(附加前提 ) (2) ( ∃x) ¬ P(x) T (1) E (3) ¬ P(a) T (2) ES (4) ( ∀x)(P(x) ∨Q(x)) P (5) P(a) ∨Q(a) T (4) US (6) Q(a) T (3)(5) I (7) ( ∃x)Q(x) T (6) EG

西安电子科技大学$2.6.1谓词逻辑推理证明方法软件学院【例题】指出下列推理中的错误,并说明理由。前提引入(1) (Vx)(P(x)-Q(x))(1), US(2) P(c)-Q(c)全称指定为个体c前提引入(3) (3x)P(x)(4) P(c)(3),ES存在指定为个体c(5) Q(c)(2), (4), T, I(5), EG(6) (3x)Q(x)
西安电子科技大学 §2.6.1 谓词逻辑推理证明方法 软件学院 全称指定为个体c 存在指定为个体c

西安电子科技大学S2.6.2谓词逻辑推理的应用软件学院家教家【例题】某旅游团去木兰围场旅游,团员们骑马、射箭、吃烤肉,最后去商店买纪念品。已知:(1)有人买了蒙古刀;(2)有人没有买蒙古刀;(3)该团的张先生和王女士都买了蒙古刀。如果以上三句话中恰有一句话为真,请判断张先生和王女士谁买了蒙古刀?解答:若第(3)句话为真。则有张先生和王女士都买了蒙古刀,那么第(1)句话也为真。这与仅有一句话为真矛盾,所以(3)为假。若(3)为假,表明张先生和王女士至少一人没有买蒙古刀,那么(2)为真,进而(1)为假,故有,“没有人买了蒙古刀”为真。所以,张先生和王女士都没有买蒙古刀
西安电子科技大学 §2.6.2 谓词逻辑推理的应用 软件学院 【例题】某旅游团去木兰围场旅游,团员们骑马、射箭、吃烤肉,最后去商 店买纪念品。已知: (1)有人买了蒙古刀; (2)有人没有买蒙古刀; (3)该团的张先生和王女士都买了蒙古刀。 如果以上三句话中恰有一句话为真,请判断张先生和王女士谁买了蒙古刀? 解答:若第(3)句话为真。 则有张先生和王女士都买了蒙古刀,那么第(1)句话也为真。这与仅 有一句话为真矛盾,所以(3)为假。 若(3)为假,表明张先生和王女士至少一人没有买蒙古刀,那么(2) 为真,进而(1)为假。 故有,“没有人买了蒙古刀”为真。 所以,张先生和王女士都没有买蒙古刀

西安电子科技大学$2.6.2i谓词逻辑推理的应用软件学院【例题符号化并推证下列结论的有效性前提:(1)每个研究生或者是推荐免试者或者是统考选拨者(2)并非每个研究生都是推荐免试者:结论:(3)有些研究生是统考选拨者。设A(α):x是研究生,B(x):x是推荐免试者,C(x):x是统考选拔者Vx(A(x) →(B(x) vC(x),-Vx(A(x) →B(x)= x(A(x) ^C(x)证明:P(1)-Vx(A(x) → B(x)(2)T (1) E3x-(A(x) → B(x)(3)T (2) Ex-(-A(x) V B(x))(4)Ex(A(x) △ -B(x))T (3) E
西安电子科技大学 §2.6.2 谓词逻辑推理的应用 软件学院 设A(x): x是研究生,B(x): x是推荐免试者,C(x):x是统考选拔者 ∨→∀ xCxBxAx )))()(()(( ,¬ ∀ ⇒→ ∃ ∧ xCxAxxBxAx ))()(())()(( 证明: (1) ¬ ∀ → xBxAx ))()(( P (2) ∃ ¬ → xBxAx ))()(( (3) ∃ ¬ ¬ ∨ xBxAx ))()(( T (1) E T (2) E (4) ∃ ∧ ¬ xBxAx ))()(( T (3) E

西安电子科技大学$2.6.2谓词逻辑推理的应用软件学院(5)A(a) ^-B(a)T (4) ES(6)A(a)T (5) I(7)-B(a)T (5) I(8)PVx(A(x) →(B(x) vC(x))(9)A(a) -→(B(a) vC(a)T (8) US(10)B(a) vC(a)T (6) (9) I(11)C(a)T (7) (10) IA(a) ^C(a)(12)T (6) (11) I(13)3x(A(x) ^C(x)T (12) EG
西安电子科技大学 §2.6.2 谓词逻辑推理的应用 软件学院 (5) (6) T (4) ES T (5) I ∧ ¬ aBaA )()( aA )( (7) T (5) I ¬ aB )( (8) ∨→∀ xCxBxAx ))()(()(( P (9) ∨→ aCaBaA ))()(()( T (8) US (10) T (6) (9) I ∨ aCaB )()( (11) aC )( T (7) (10) I (12) ∧ aCaA )()( T (6) (11) I (13) ∃ ∧ xCxAx ))()(( T (12) EG