
西安电子科技大学离散数学软件学院第二篇集合论第4章函数与无限集合4.1函数的概念第21课时第22课时4.2复合函数和逆函数4.3可数与不可数集合第23课时第24课时4.4集合基数的比较
西安电子科技大学 离散数学 软件学院 第二篇 集合论 第21课时 4.1 函数的概念 第4章 函数与无限集合 4.3 可数与不可数集合 4.2 复合函数和逆函数 4.4 集合基数的比较 第22课时 第23课时 第24课时
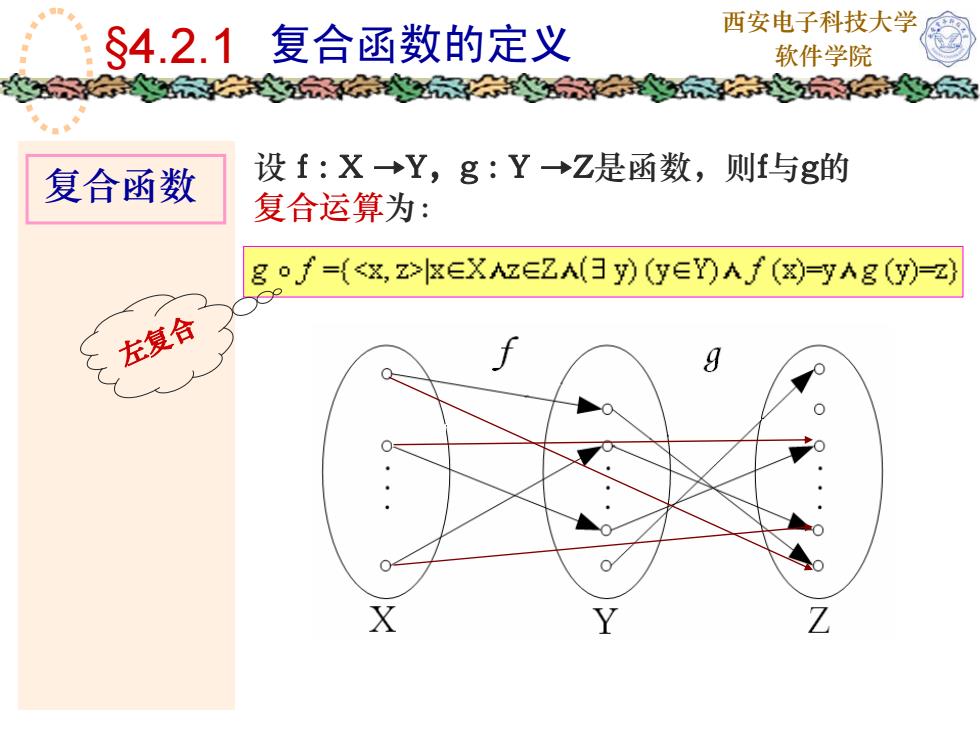
西安电子科技大学复合函数的定义$4.2.1软件学院家设f:X-→Y,g:Y-→Z是函数,则f与g的复合函数复合运算为:g o -((xEXAZEZA(Ey) (YEY)AJ (X)-yAg(Y)-z)左复合9CXYZ
西安电子科技大学 复合函数的定义 软件学院 复合函数 §4.2.1 设 f : X →Y,g : Y →Z是函数,则f与g的 复合运算为: 左复合

西安电子科技大学S4.2.1复合函数的定义软件学院茶教家家家『定理』设f:X→Y,g:Y一→Z是函数,则gf是从X到乙的函数。证明:因为f是从X到Y的函数,则有任取xEX存在唯一的yEY,满足f(α)=y。又因为g是从Y到Z的函数,则对于y存在唯一的zEZ,满足g(y)=z所以对于xEX,存在唯一的zEZ,使得gf(α)=z。故gf是从X到Z的函数
西安电子科技大学 §4.2.1 复合函数的定义 软件学院 『定理』设f : X →Y,g : Y →Z是函数,则g◦f是从X 到Z的函数。 证明:因为f是从X到Y的函数,则有任取x∈X, 存在唯一的y∈Y,满足f(x)=y。又因为g是从Y到Z的函数,则 对于y存在唯一的z∈Z,满足g(y)=z。 所以对于x∈X,存在唯一的z∈Z,使得g◦f(x)=z。 故 g◦f是从X到Z的函数
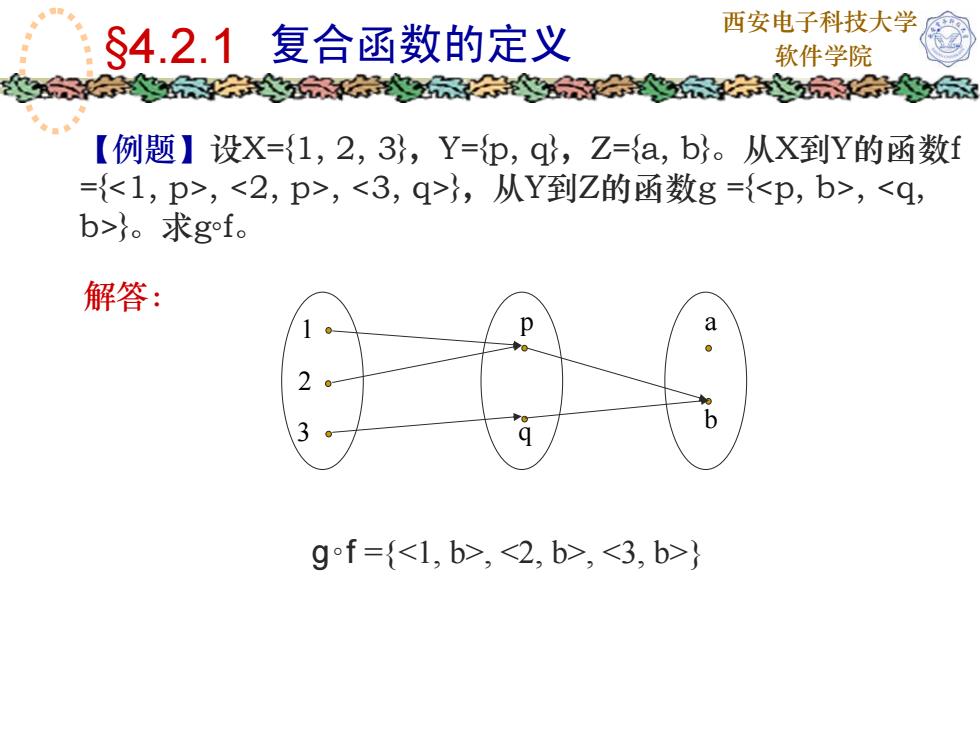
西安电子科技大学$4.2.1复合函数的定义软件学院【例题】设X=(1,2,3),Y=(p,q,Z=(a,b}。从X到Y的函数f=(,,),从Y到Z的函数g =(,}。求gof。解答:gf =[, , ]
西安电子科技大学 §4.2.1 复合函数的定义 软件学院 【例题】设X={1, 2, 3},Y={p, q},Z={a, b}。从X到Y的函数f ={, , },从Y到Z的函数g ={, }。求g◦f。 1 2 3 p q a b 解答: g ◦f ={, , }

西安电子科技大学S4.2.1复合函数的定义软件学院教家【例题】设R为实数集合,对xER有f(x)=x+2,g(x)=x-1, 求gof。解答:任取xER,x在函数f下的映象f(x)=x+2,而x+2在函数g下的映象为(x+2)=x+2-1=x+1。所以gof(x)=x+1
西安电子科技大学 §4.2.1 复合函数的定义 软件学院 【例题】设R为实数集合,对x∈R有f(x)=x+2, g(x)=x-1,求g◦f。 解答:任取x∈R,x在函数f下的映象f(x)=x+2, 而x+2在函数g下的映象为(x+2)=x+2-1=x+1。 所以g◦f(x)=x+1
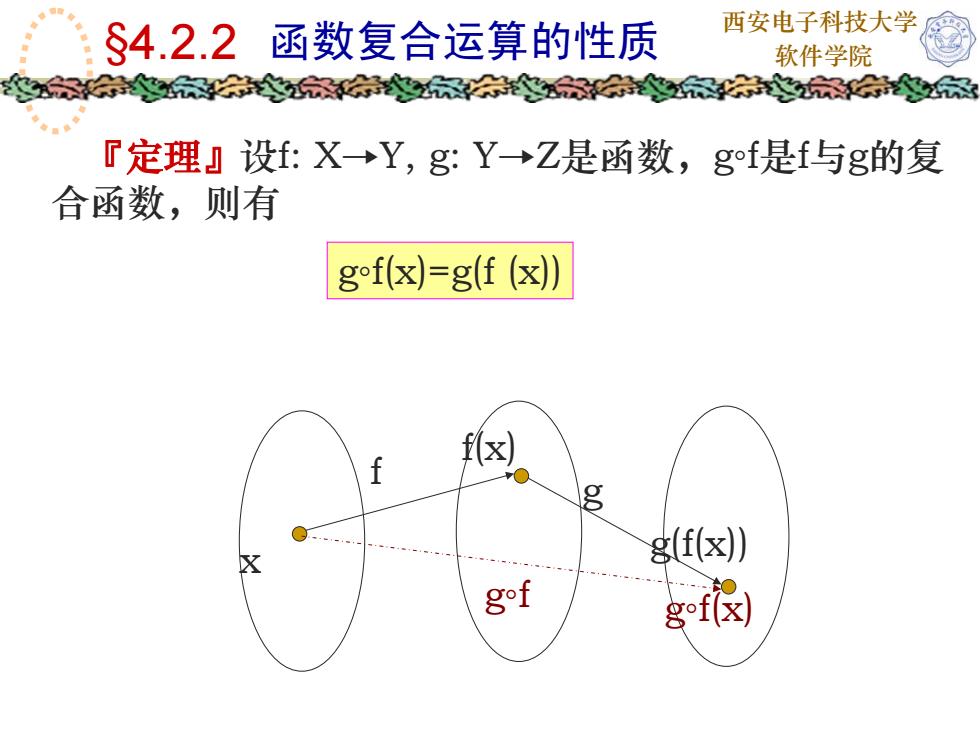
西安电子科技大学$4.2.2函数复合运算的性质软件学院教家家家『定理』设f:X→Y,g:Y→Z是函数,gf是f与g的复合函数,则有gof(x)=g(f (μ)g(f(x)Xgofgof(α)
西安电子科技大学 §4.2.2 函数复合运算的性质 软件学院 『定理』设f: X→Y, g: Y→Z是函数,g◦f是f与g的复 合函数,则有 g◦f(x)=g(f (x)) f g g◦f x f(x) g(f(x)) g◦f(x)
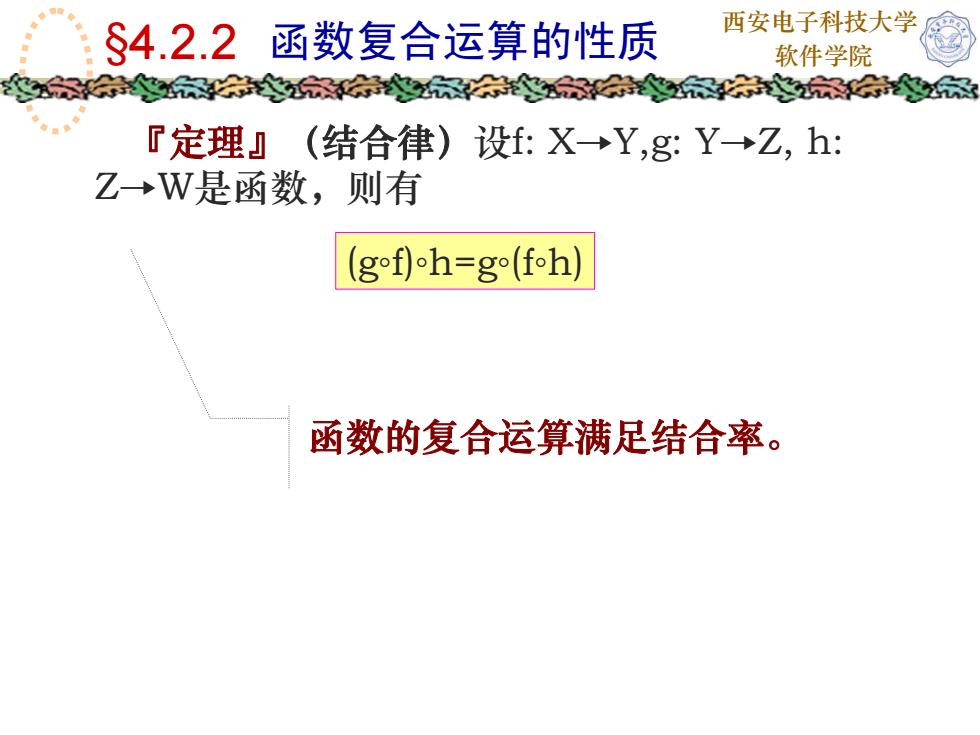
西安电子科技大学$4.2.2i函数复合运算的性质-软件学院茶家家教家家『定理』(结合律)设f:X→Y,g:Y→Z,h:Z→W是函数,则有(gof)h=g(foh)函数的复合运算满足结合率
西安电子科技大学 §4.2.2 函数复合运算的性质 软件学院 『定理』(结合律)设f: X→Y,g: Y→Z, h: Z→W是函数,则有 (g◦f)◦h=g◦(f◦h) 函数的复合运算满足结合率

西安电子科技大学$4.2.2函数复合运算的性质软件学院家教水教办茶教『定理』设f:X→Y,g:Y→Z是函数,gof是f与g的复合函数。(a)若g和f是满射的,则gof是满射的;(b)若g和f是单射的,则gof是单射的;(c)若g和f是双射的,则gf是双射的。两个满射函数的复合函数还是满射函数;两个单射函数的复合函数还是一个单射函数
西安电子科技大学 §4.2.2 函数复合运算的性质 软件学院 两个满射函数的复合函数还是满射函数;两个 单射函数的复合函数还是一个单射函数 。 『定理』设f: X→Y,g: Y→Z是函数,g◦f是f与g 的复合函数。 (a)若g和f是满射的,则g◦f是满射的; (b)若g和f是单射的,则g◦f是单射的; (c)若g和f是双射的,则g◦f是双射的

西安电子科技大学S4.2.2函数复合运算的性质软件学院『定理』设f:X→Y,g:Y-Z是函数,gf是f与g的复合函数(a)若gf是满射的,则g是满射的;(b)若gof是单射的,则f是单射的:(c)若gof是双射的,则g是满射的且f是单射的。证明:(a)若gf是满射的,则任取zEZ,存在xEX,使得gof(x)=Z,即g(f(x)=Z。设f(x)=y EY,因此存在y使得g (y)=z由于z是任意的,所以g是满射
西安电子科技大学 §4.2.2 函数复合运算的性质 软件学院 『定理』设f: X→Y,g: Y→Z是函数,g◦f是f与g的复合函数。 (a)若g◦f是满射的,则g是满射的; (b)若g◦f是单射的,则f是单射的; (c)若g◦f是双射的,则g是满射的且f是单射的。 证明:(a)若g◦f是满射的,则任取z∈Z,存在x∈X,使得 g◦f(x)=z,即g(f(x))=z。设f(x)=y∈Y,因此存在y使得g (y)=z。 由于z是任意的,所以g是满射

西安电子科技大学$4.2.2 区函数复合运算的性质软件学院家家教家家教教家教家务『定理』设f:X→Y,g:Y→Z是函数,gf是f与g的复合函数a)若gf是满射的,则g是满射的;(b)若gof是单射的,则f是单射的;(c)若gof是双射的,则g是满射的且f是单射的。证明(b)(反证法)g°f是单射的,假设f不是单射的,则存在Xj,X2EX,X,≠X2,且有f (x)=f(x2)。又因为g是函数,所以存在z,使得g (f (区,))=g (f (x2))=z,即gof(x)=gof (x2)=z。这与gf是单射矛盾。所以是单射的
西安电子科技大学 §4.2.2 函数复合运算的性质 软件学院 『定理』设f: X→Y,g: Y→Z是函数,g◦f是f与g的复合函数。 (a)若g◦f是满射的,则g是满射的; (b)若g◦f是单射的,则f是单射的; (c)若g◦f是双射的,则g是满射的且f是单射的。 证明(b)(反证法)g◦f是单射的,假设f不是单射的,则存在 x 1, x 2∈X,x 1≠x 2,且有f (x 1)=f (x 2)。又因为g是函数,所以 存在z,使得g (f (x 1))=g (f ( x 2))=z,即g◦f ( x 1)=g◦f (x 2)=z。这 与g◦f是单射矛盾。所以f是单射的