
非孩性方程的近侧解法 ·简介 ·有根的区间确定 ·二分法 ·迭代法
非线性方程的近似解法 • 简介 • 有根的区间确定 • 二分法 • 迭代法

非线性方程的近似解法 ·简介 ·有根的区间确定 ·二分法 ·送代法
非线性方程的近似解法 • 简介 • 有根的区间确定 • 二分法 • 迭代法

非线性方程简介 x-asin x=b 一般无 超越方程 法求出 e"-sin x 0 精确解 f(x)=x”+ax1+a,x"-2+.+anx+an=0 高次代数方程 当n>4时,方程没有精确的求根公式
非线性方程简介 ( ) 1 0 2 2 1 = + 1 + + + − + = − − n n n n n f x x a x a x a x a 当n>4时,方程没有精确的求根公式。 高次代数方程 x −asin x = b e −sin x = 0 x 超越方程 一般无 法求出 精确解

非孩性方程的近似解法 ·简介 ·有根的区间确定 ·二分法 ·迭代法
非线性方程的近似解法 • 简介 • 有根的区间确定 • 二分法 • 迭代法

根的存在性 连续函数: 若f(x)∈C[a,b],且f(a)f(b)<0, 则方程f(x)=0在[a,b]内至少有一个根
连续函数: 根的存在性 则方程 在 内至少有一个根。 若 且 ( ) 0 [ , ] ( ) [ , ], ( ) ( ) 0, f x a b f x C a b f a f b =

根的区间搜索 常用方法: (1)作图法 作出y=f(x)的粗略图形,据此给出y=f(x)与 X轴交点的大致位置
常用方法: 根的区间搜索 (1)作图法 作出y=f(x)的粗略图形,据此给出y=f(x)与 x轴交点的大致位置

根的区间搜索 常用方法: 如何选取? (2)逐步搜索法 适当选取某一区间[a,b 从xo=a出发,以步长h=(b-a)N逐点计算 xk=a+kh处的函数值f(xk)。(与作图法类似) 当f(仪x)与f(k+1)异号时,[Xk,Xk+]为方程fX)=0 的一个有根区间
常用方法: 根的区间搜索 (2)逐步搜索法 适当选取某一区间[a,b], 从x0=a出发,以步长h=(b-a)/N逐点计算 xk=a+kh处的函数值f(xk )。(与作图法类似) 如何选取? 当f(xk )与f(xk+1)异号时,[xk ,xk+1]为方程f(x)=0 的一个有根区间

n次代数方程根的上下界 f(x)=x”+ax1+a,x"-2+.+an-x+an=0 (l)令a=max{apla,la, 则以上方程的根的绝对值小于a+1。 (2)令b=1 xt1,a,a,la, a 则以上方程的根的绝对值大于 b+1
n次代数方程根的上下界 ( ) 1 0 2 2 1 = + 1 + + + − + = − − n n n n n f x x a x a x a x a 则以上方程的根的绝对值小于 。 令 , , , 1 (1) max{ }, 1 2 + = a a a a a n 则以上方程的根的绝对值大于 。 , , , , 令 1 1 , max{1 } (2) 1 2 1 + = − b a a a a b n n

例3.1求方程x3.1.8x2+0.15x+0.65=0的 根模的上下界及一个有根区间。 解:(1)求根模上下界 a=max{ala,p,a.}=max1.8,l0.15,0.65l}=1.8 6、 max{1,a,aa,.}max{1,|-1.8,10.15 1.8 a 0.65 0.65 根模的上下界由以下不等式给出 a+1>x 6+ 即2.8>x> 1.8 ≈0.2653 +1 0.65
例3.1 求方程x 3 -1.8x2+0.15x+0.65=0的 根模的上下界及一个有根区间。 max{ } (1) a a1 , a2 , , an 解: 求根模上下界 = = max{ −1.8, 0.15, 0.65}=1.8 an a a a b max{1, } 1 , 2 ,, n-1 = 0.65 1.8 0.65 max{1 1.8 0.15} = − = , , 0.2653 1 0.65 1.8 1 .8 1 1 1 + + + x b a x 即2 根模的上下界由以下不等式给出
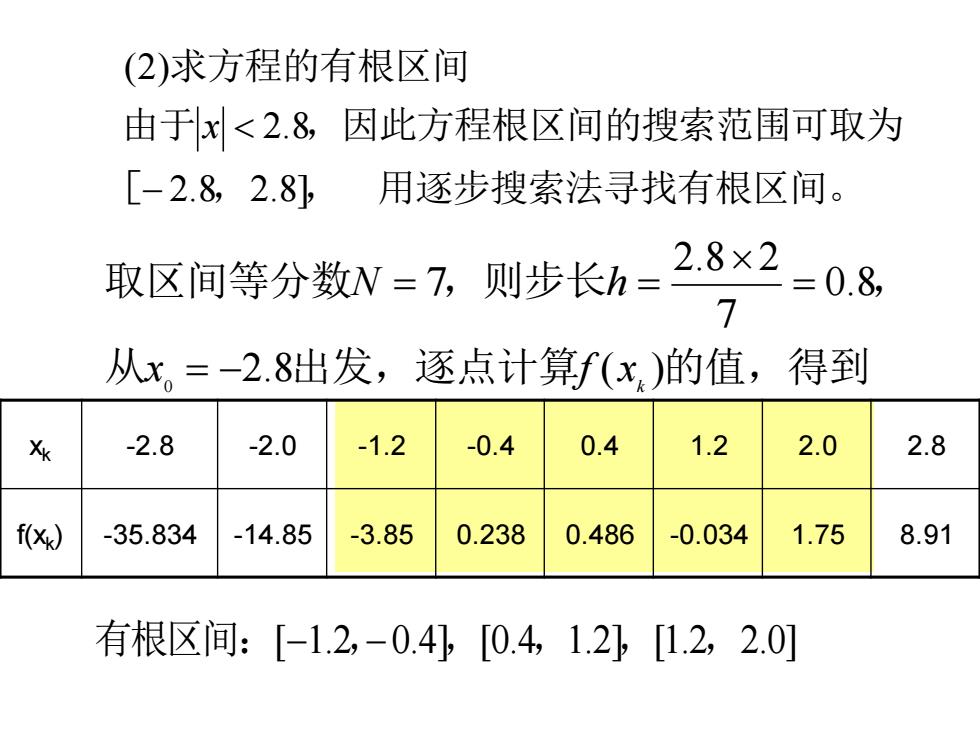
(2)求方程的有根区间 由于x<2.8,因此方程根区间的搜索范围可取为 [-2.8,2.8] 用逐步搜索法寻找有根区间。 取区间等分数N=7,则步长h= 2.8×2 =0.8, 7 从x,=-2.8出发,逐点计算f(x)的值,得到 Xk -2.8 -2.0 -1.2 -0.4 0.4 1.2 2.0 2.8 f(Xx) -35.834 -14.85 -3.85 0.238 0.486 -0.034 1.75 8.91 有根区间:「-1.2,-0.4[0.4,1.2[1.2,2.0]
[ , , 用逐步搜索法寻找有根区间。 由于 ,因此方程根区间的搜索范围可取为 求方程的有根区间 2.8 2.8] 2.8 (2) − x 从 出发,逐点计算 的值,得到 取区间等分数 ,则步长 , 2.8 ( ) 0.8 7 2.8 2 7 0 k x f x N h = − = = = xk -2.8 -2.0 -1.2 -0.4 0.4 1.2 2.0 2.8 f(xk ) -35.834 -14.85 -3.85 0.238 0.486 -0.034 1.75 8.91 有根区间: [−1.2,−0.4], [0.4, 1.2], [1.2, 2.0]