
概率论与数理统计 机电工程学院机电所 杨东武
概率论与数理统计 机电工程学院机电所 杨东武

“概率论与数理统计”教学大纲 课程编号:SC12005 课程名称:概率论与数理统计 英文名称:Probability and Statistics 学时:46 学分:3 课程类型:必修 课程性质:公共基础课 适用专业:工科类专业 先修课程:高等数学 开课学期:第2学期 开课院系:理学院数学系 一、课程的教学日标与任务 概率论与数理统计是我校工科各专业的共同必修课。它是一门研究随机现象规律的数学学 科,理论严谨、应用广泛,是数学的一个重要分支,也是现代科技人才必须掌握的工具技术 课之一。通过该课程的学习,要使学生系统地获得概率论与数理统计的基本知识,必要的基 础理论:要求学生掌握常用的分析方法:同时为学习随机过程,信号处理等后继课程奠定基 础。 二、本课程与其它课程的联系和分工 概率论与数理统计是研究随机现象的入门课程,是现代科技人才必须掌握的工具技术课之 ,也是学习随机过程、信号处理等后继课程的主要数学工具 三、课程内容及基本要求 (一)概率论的基本概念(8学时) 内容:随机实验:样本空间。随机事件:频率概率:古典概:条件概率与独立性。 1.基本要求 ()理解样本空间,随机事件的概念,掌握事件的关系及运算。能熟练运用事件的和、积、 差运算表示未知的事件。 (2)了解概率的公理化体系,掌握概率的基本性质。熟练掌握概率的加法公式。会计算古典 概型问的概率。 (3)了解条件概率的概念,掌握概率的乘法公式、全概率公式和Bays公式。 (④)了解事件独立性的概念,掌握用事件独立性进行概率计算。 2.重点、难点 重点:样本空间,随机事件:事件的关系及运算:概率的基本性质:条件概率,概率的乘法
“概率论与数理统计”教学大纲 课程编号:SC1112005 课程名称:概率论与数理统计 英文名称:Probability and Statistics 学 时:46 学 分:3 课程类型:必修 课程性质:公共基础课 适用专业:工科类专业 先修课程:高等数学 开课学期:第 2 学期 开课院系:理学院数学系 概率论与数理统计是我校工科各专业的共同必修课。它是一门研究随机现象规律的数学学 科,理论严谨、应用广泛,是数学的一个重要分支,也是现代科技人才必须掌握的工具技术 课之一。通过该课程的学习,要使学生系统地获得概率论与数理统计的基本知识,必要的基 础理论;要求学生掌握常用的分析方法;同时为学习随机过程,信号处理等后继课程奠定基 础。 概率论与数理统计是研究随机现象的入门课程,是现代科技人才必须掌握的工具技术课之 一,也是学习随机过程、信号处理等后继课程的主要数学工具。 (一) 概率论的基本概念(8 学时) 内容:随机实验;样本空间,随机事件;频率概率;古典概型;条件概率与独立性。 1.基本要求 (1) 理解样本空间,随机事件的概念,掌握事件的关系及运算。能熟练运用事件的和、积、 差运算表示未知的事件。 (2) 了解概率的公理化体系,掌握概率的基本性质。熟练掌握概率的加法公式。会计算古典 概型问题的概率。 (3) 了解条件概率的概念,掌握概率的乘法公式、全概率公式和 Bayes 公式。 (4) 了解事件独立性的概念,掌握用事件独立性进行概率计算。 2. 重点、难点 重点:样本空间,随机事件;事件的关系及运算;概率的基本性质;条件概率,概率的乘法

公式、全概公式和Bayes公式:独立性的概念。 难点:古典概型问题的概率。 3.说明 几何概型可以选讲 (二)随机变量及其分布(6学时) 内容:随机变量:离散型随机变量的概率分布:随机变量的分布函数:连续型随机变量的制 率密度函数:随机变量的函数的分布。 1.基本要水 ()理解随机变量,离散型随机变量的概念,理解独立重复试验的概念。掌握计算有关事件 概率的方法。掌握0-1分布,掌握Poisson分布及其应用,掌握二项分布及其应用。 (2)了解分布函数的概念,理解连续性随机变量及其概率密度的概念。掌握概率密度与分布 函数的关系,分布函数与密度函数的性质,掌均匀分布和指数分布及其应用。 (3)掌握正 态分 布及其应用,会求简单随机变量函数的概率分布 2.重点、难点 重点:随机变量的概念:离散型随机变量的分布律,常见的离散型随机变量二项分布,Poisso 分布,Bernoulli概型:分布函数的概念及性质:概常密度函数的性质,常见的连续型随机变 量,均匀分布,指数分布,正态分布:随机变量函数的分布。 难点:随机变量的概念:分布函数的概念 (三)多维随机变量及其分布(8学时) 内容:二维随机变量:边际分布:条件分布:相互独立的随机变量:两个随机变量的函数的 分布。 1。其木要求 ()了解二维随机变量的概念,理解二维随机变量的联合分布函数的概念及性质,理解二维 离散型随机变量的联合分布律及性质,二维连续型随机变量的联合密度函数及性质,会利用 二维概率分布求有关事件的概率。 (2②)了解边缘分布,条件分布。理解边缘密度,条件密度。会求二维离散型随机变量的边缘 分布,边缘分布 。会求 维连续型随机变量的边缘分布,边缘密度 (③)理解随机变量独立性的概念,掌握离散型和连续型随机变量独立性的条件 (④)掌握二维均匀分布,了解二维正态分布的概率密度,理解其中参数的概率意义。 (⑤)会求两个随机变量的简单函数的分布。 2.重点、难点 重点: 二维随机变量联合分布函数的概念,二维离散型随机变量的联合分布律,二维连续基 随机变量的联合密度函数:边际分布,二维离散型随机变量的边际分布律,二维连续型随机 变量的边际密度函数:离散型随机变量相互独立的充要条件,连续型随机变量相互独立的充 要条件。 难点:离散型随机变量的条件分布律,连续型随机变量的条件密度函数:两个随机变量和的 密度函数,两个随机变量商的密度函数。 (四)随机变量的数字特征(6学时) 内容:数学期望:方差几种重要随机变量的数学期望和方差:协方差及相关系数:矩、协 方差矩阵。 1.基本要求 ()理解随机变量的数字特征(数学期望、方差、标准差、协方差、相关系数)的概念,并会
公式、全概公式和 Bayes 公式;独立性的概念。 难点:古典概型问题的概率。 3. 说明 几何概型可以选讲。 (二) 随机变量及其分布(6 学时) 内容:随机变量;离散型随机变量的概率分布;随机变量的分布函数;连续型随机变量的概 率密度函数;随机变量的函数的分布。 1. 基本要求 (1) 理解随机变量,离散型随机变量的概念,理解独立重复试验的概念。掌握计算有关事件 概率的方法。掌握 0-1 分布,掌握 Poisson 分布及其应用,掌握二项分布及其应用。 (2) 了解分布函数的概念,理解连续性随机变量及其概率密度的概念。掌握概率密度与分布 函数的关系,分布函数与密度函数的性质,掌握均匀分布和指数分布及其应用。 (3) 掌握正态分布及其应用,会求简单随机变量函数的概率分布。 2. 重点、难点 重点:随机变量的概念;离散型随机变量的分布律,常见的离散型随机变量二项分布,Poisson 分布,Bernoulli 概型;分布函数的概念及性质;概率密度函数的性质,常见的连续型随机变 量,均匀分布,指数分布,正态分布;随机变量函数的分布。 难点:随机变量的概念;分布函数的概念。 (三) 多维随机变量及其分布(8 学时) 内容:二维随机变量;边际分布;条件分布;相互独立的随机变量;两个随机变量的函数的 分布。 1. 基本要求 (1) 了解二维随机变量的概念,理解二维随机变量的联合分布函数的概念及性质,理解二维 离散型随机变量的联合分布律及性质,二维连续型随机变量的联合密度函数及性质,会利用 二维概率分布求有关事件的概率。 (2) 了解边缘分布,条件分布。理解边缘密度,条件密度。会求二维离散型随机变量的边缘 分布,边缘分布律。会求二维连续型随机变量的边缘分布,边缘密度。 (3) 理解随机变量独立性的概念,掌握离散型和连续型随机变量独立性的条件。 (4) 掌握二维均匀分布,了解二维正态分布的概率密度,理解其中参数的概率意义。 (5) 会求两个随机变量的简单函数的分布。 2. 重点、难点 重点:二维随机变量联合分布函数的概念,二维离散型随机变量的联合分布律,二维连续型 随机变量的联合密度函数;边际分布,二维离散型随机变量的边际分布律,二维连续型随机 变量的边际密度函数;离散型随机变量相互独立的充要条件,连续型随机变量相互独立的充 要条件。 难点:离散型随机变量的条件分布律,连续型随机变量的条件密度函数;两个随机变量和的 密度函数,两个随机变量商的密度函数。 (四) 随机变量的数字特征(6 学时) 内容:数学期望;方差;几种重要随机变量的数学期望和方差;协方差及相关系数;矩、协 方差矩阵。 1. 基本要求 (1) 理解随机变量的数字特征(数学期望、方差、标准差、协方差、相关系数)的概念,并会

运用数字特征的基本性质计算具体分布的数字特征,掌握常用分布的数字特征。 (2)会根据随机变量X的联合概率分布求其函数8)的数学期望Eg:会根据随机变量X 和Y的概率分布求其函数g(X,的数学期望Eg(X,。 (3)根据随机变量X和Y的概率分布求其相关系数,理解相关系数取特殊值的概率含义。了 解切比雪夫不等式。 2.重点、难点 重点:离散型随机变量的数学期望,连续型随机变量的数学期望,随机变量函数的数学期望 数学期望的性质,几种重要随机变量的数学期望:方差的概念,方差的性质,几种重要随机 弯量的方差:协方劳,相关系数。 3.说明 矩、协方差矩阵的概念可以略讲。 (五)大数定律及中心极限定理(2学时) 内容:大数定律:中心极限定理。 1.基本要求 (1)了解切比雪夫大数定律、贝努利大数定律和辛锌大数定律(独立同分布随机变量的大数定 律)成立的条件和结论。 (2)了解独立同分布的中心极限定理,德莫佛一拉普拉斯中心极限定理(二项分布以正态分布 为极限分布的定理)的应用条件和结论,并会用相关定理近似计算有关随机事件的 概率。 2.重点、难点 重点:独立同分布的中心极限定理:德莫佛一拉普拉斯中心极限定理。 难点:概率收敛的概念:切比雪夫大数定律、贝努利大数定律、辛锌大数定律。 3.说明 该章大数定理部分可以略讲。 (六)数理统计的基本概念(3学时) 内容:随机样本:抽样分布。 基本要求 ()了解总体、个体、样本、简单随机样本、统计量、样本均值、样本方差及样本矩的概念。 了解x2分布、1分布和F分布的定义及性质、了解分位数的概念并会查表计算。 (2)了解正态总体的常用抽样分布。 2.重点 总体、个体、样本、简单随机样本、统计量、样本均值、样本方差及样本矩的概念:正态总 体的常用抽样分布。 3.说明 分布、1分布和F分布的定义及性 可略讲 (七)参数的点估计与区间估计7学时) 内容:参数的点估计:估计量的评价标准:区间估计:正态总体均值和方差的置信 区间:(0-1)分布参数的区间估计:单侧置信区间。 1.基本要求 ()理解参数的估计、估计量、点估计的概念。掌握矩估计法一,二阶矩)和极大似然估计 法。 (2)了解估计量的无偏性、有效性(最小方差性)和一致性相合性)的概念,并会验证估计量的 无偏性
运用数字特征的基本性质计算具体分布的数字特征,掌握常用分布的数字特征。 (2) 会根据随机变量 X 的联合概率分布求其函数 g(X)的数学期望 E[g(X)];会根据随机变量 X 和 Y 的概率分布求其函数 g(X,Y)的数学期望 E[g(X,Y)]。 (3) 根据随机变量 X 和 Y 的概率分布求其相关系数,理解相关系数取特殊值的概率含义。了 解切比雪夫不等式。 2. 重点、难点 重点:离散型随机变量的数学期望,连续型随机变量的数学期望,随机变量函数的数学期望, 数学期望的性质,几种重要随机变量的数学期望;方差的概念,方差的性质,几种重要随机 变量的方差;协方差,相关系数。 3. 说明 矩、协方差矩阵的概念可以略讲。 (五) 大数定律及中心极限定理(2 学时) 内容:大数定律;中心极限定理。 1.基本要求 (1) 了解切比雪夫大数定律、贝努利大数定律和辛锌大数定律(独立同分布随机变量的大数定 律)成立的条件和结论。 (2) 了解独立同分布的中心极限定理,德莫佛—拉普拉斯中心极限定理(二项分布以正态分布 为极限分布的定理) 的应用条件和结论,并会用相关定理近似计算有关随机事件的 概率。 2. 重点、难点 重点:独立同分布的中心极限定理;德莫佛—拉普拉斯中心极限定理。 难点:概率收敛的概念;切比雪夫大数定律、贝努利大数定律、辛锌大数定律。 3.说明 该章大数定理部分可以略讲。 (六) 数理统计的基本概念(3 学时) 内容:随机样本;抽样分布。 1. 基本要求 (1) 了解总体、个体、样本、简单随机样本、统计量、样本均值、样本方差及样本矩的概念。 了解 x 2 分布、t 分布和 F 分布的定义及性质、了解分位数的概念并会查表计算。 (2) 了解正态总体的常用抽样分布。 2. 重点 总体、个体、样本、简单随机样本、统计量、样本均值、样本方差及样本矩的概念;正态总 体的常用抽样分布。 3.说明 x 2 分布、t 分布和 F 分布的定义及性质可略讲。 (七) 参数的点估计与区间估计(7 学时) 内容:参数的点估计;估计量的评价标准;区间估计;正态总体均值和方差的置信 区间;(0-1)分布参数的区间估计;单侧置信区间。 1.基本要求 (1) 理解参数的估计、估计量、点估计的概念。掌握矩估计法(一,二阶矩)和极大似然估计 法。 (2) 了解估计量的无偏性、有效性(最小方差性)和一致性(相合性)的概念,并会验证估计量的 无偏性
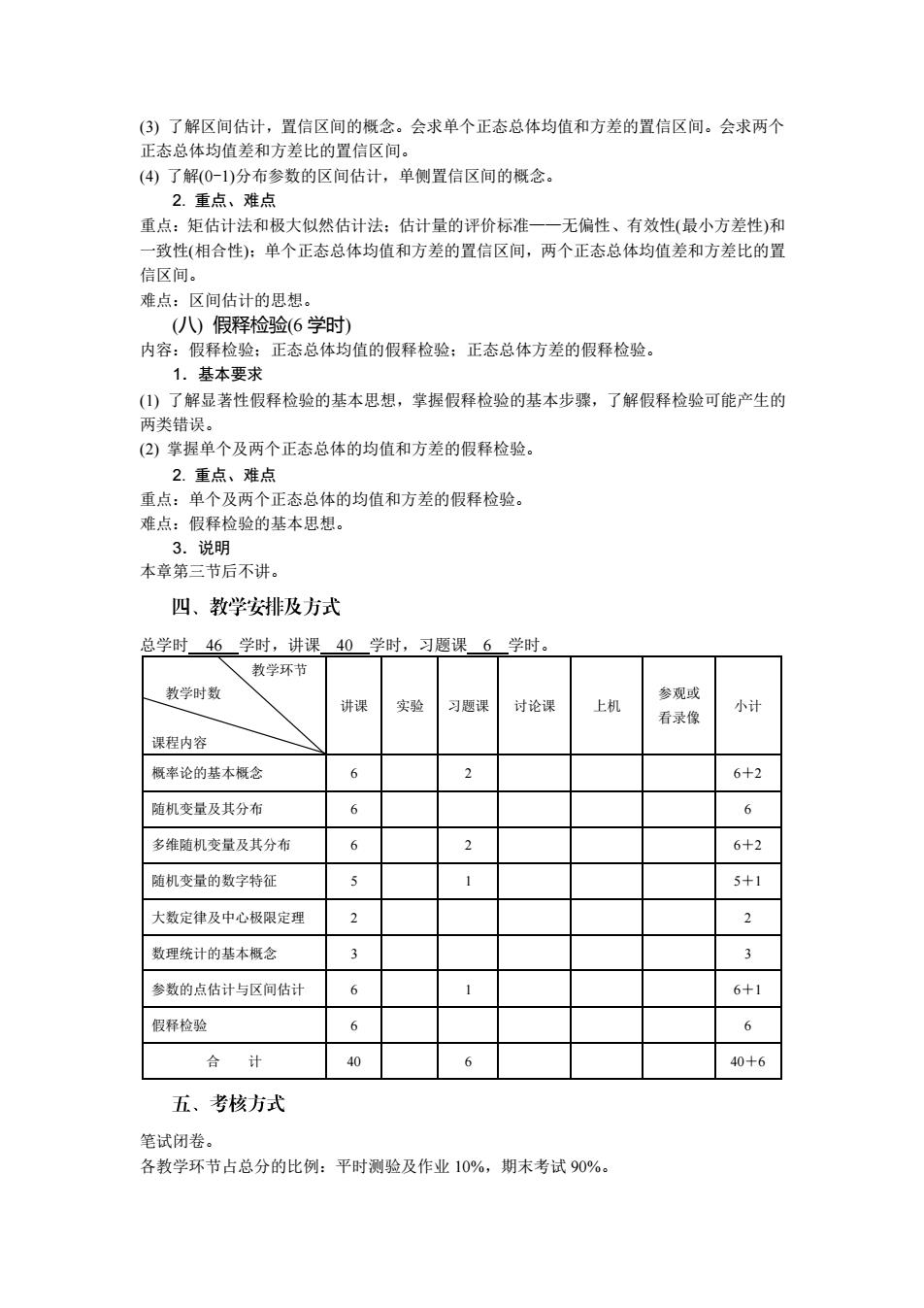
(3)了解区间估计,置信区间的概念。会求单个正态总体均值和方差的置信区间。会求两个 正态总体均值差和方差比的置信区间。 (④)了解(0-)分布参数的区间估计,单侧置信区间的概念。 2.重点、难点 重点:矩估计法和极大似然估计法:估计量的评价标准一一无偏性、有效性(最小方差性)和 一致性(相合性):单个正态总体均值和方差的置信区间,两个正态总体均值差和方差比的置 信区间。 难点:区间估计的思想。 (八)假释检验(6学时) 内容:假释检验:正态总体均值的假释检验:正态总体方差的假释检验。 1.基本要求 (1)了解显著性假释检验的基本思想,掌握假释检验的基本步骤,了解假释检验可能产生的 两类错误。 (2)掌握单个及两个正态总体的均值和方差的假释检验。 2.重点、难点 重点:单个及两个正态总体的均值和方差的假释检验。 难点:假释检验的基本思想。 3.说明 本章第三节后不讲。 四、教学安排及方式 总学时46学时,讲课40学时,习题课6学时。 、教学环节 、教学时数 参或 讲课 实验 习题讲 讨论课 上机 看录像 小计 课程内容 概率论的基本概念 6 6+2 随机变量及其分布 6 6 多维随机变量及其分布 6 2 6+2 随机变量的数字特征 1 5+1 大数定律及中心极限定理 2 2 数理统计的基本概念 3 3 参数的点估计与区间估计 6 6+1 假释检验 6 6 合计 40 6 40+6 五、考核方式 笔试闭卷。 各教学环节占总分的比例:平时测验及作业10%,期末考试90%
(3) 了解区间估计,置信区间的概念。会求单个正态总体均值和方差的置信区间。会求两个 正态总体均值差和方差比的置信区间。 (4) 了解(0-1)分布参数的区间估计,单侧置信区间的概念。 2. 重点、难点 重点:矩估计法和极大似然估计法;估计量的评价标准——无偏性、有效性(最小方差性)和 一致性(相合性);单个正态总体均值和方差的置信区间,两个正态总体均值差和方差比的置 信区间。 难点:区间估计的思想。 (八) 假释检验(6 学时) 内容:假释检验;正态总体均值的假释检验;正态总体方差的假释检验。 1.基本要求 (1) 了解显著性假释检验的基本思想,掌握假释检验的基本步骤,了解假释检验可能产生的 两类错误。 (2) 掌握单个及两个正态总体的均值和方差的假释检验。 2. 重点、难点 重点:单个及两个正态总体的均值和方差的假释检验。 难点:假释检验的基本思想。 3.说明 本章第三节后不讲。 总学时 46 学时,讲课 40 学时,习题课 6 学时。 教学环节 教学时数 课程内容 讲课 实验 习题课 讨论课 上机 参观或 看录像 小计 概率论的基本概念 6 2 6+2 随机变量及其分布 6 6 多维随机变量及其分布 6 2 6+2 随机变量的数字特征 5 1 5+1 大数定律及中心极限定理 2 2 数理统计的基本概念 3 3 参数的点估计与区间估计 6 1 6+1 假释检验 6 6 合 计 40 6 40+6 笔试闭卷。 各教学环节占总分的比例:平时测验及作业 10%,期末考试 90%

六、推荐教材与参考资料 教材 盛骤,等.概率论与数理统计.北京:高等教有出版社,1989 参考资料: [复且大学.概率论.北京:人民教有出版社,1979 [2复旦大学数理统计.北京:人民教育出版社,1979 [3)王梓坤.概率论及其应用.北京:科学出版社,1979 (执笔人:宋月审核人:于力)
教材: 盛骤,等. 概率论与数理统计. 北京:高等教育出版社,1989 参考资料: [1] 复旦大学. 概率论. 北京:人民教育出版社,1979 [2] 复旦大学. 数理统计. 北京:人民教育出版社,1979 [3] 王梓坤. 概率论及其应用. 北京:科学出版社,1979 (执笔人:宋 月 审核人:于 力)

第一讲随机事件与概率 概率论与数理统计 1.概率论是研究什么的? 第一章概率论的基本概念 研究和揭示随机现象统计规律性的科学。 §1随机试验 随机现象:是在个别试验中结果呈现不确定 自然界和补会上发生的现象是名利 类现为确岸性现象 性,但在大量重复试验中结果又具有统计规 多样的,有 在一定条件下必然发生的现象 律性的现象。 向空中抛一物体必然落向地面: 水加热到100℃必然沸腾: 2.随机试验(E):具有以下特点的试验称 异性电荷相吸引: 为随机试验。 放射性元素发生蜕变: 特点: (1).可在相同条件下重复进行: 还有一类为随机现象:在试验或 (2).试验可能结果不止一个,但能确定所有 观察前无法预知出现什么结果。 的可能结果: 抛一枚硬币结果可能正面(或反 (3),一次试验之前无法确定具体是哪种结 面)嘲上: 果出现。 向同一目标射击,各次弹着点都 例1: 不相同: E1抛一枚硬币,分别用“H”和“T”表某地区的日平均气温: 示出正面和反面: 掷一颗骰子,可能出现的点数: E2:将一枚硬币连抛三次,考虑正反面出现 的情况: E3:将一枚硬币连抛三次,考虑正面出现的 统计规律性: 多次重复抛一枚硬币得到正面 次数 朝上的结果大致有一半: E4:掷一颗骰子时出现的点数: 同一门大炮射击同一目标的着 E5:记录电话交换台一分钟内接到的呼唤 弹点大致在目标附近且按照一 次数: 定的规律分布: E6:在一批灯泡中任取一只,测试其寿命: E7:记录某地一昼夜的最高温度与最低温 度
第一讲 随机事件与概率 1.概率论是研究什么的? 研究和揭示随机现象 统计规律性的科学。 随机现象:是在个别试验中结果呈现不确定 性,但在大量重复试验中结果又具有统计规 律性的现象。 2. 随机试验(E):具有以下特点的试验称 为随机试验。 特点: (1).可在相同条件下重复进行; (2).试验可能结果不止一个,但能确定所有 的可能结果; (3).一次试验之前无法确定具体是哪种结 果出现。 例1: E1: 抛一枚硬币,分别用“H” 和“T” 表 示出正面和反面; E2: 将一枚硬币连抛三次,考虑正反面出现 的情况; E3: 将一枚硬币连抛三次,考虑正面出现的 次数; E4: 掷一颗骰子时出现的点数; E5: 记录电话交换台一分钟内接到的呼唤 次数; E6: 在一批灯泡中任取一只,测试其寿命; E7: 记录某地一昼夜的最高温度与最低温 度 。 概率论与数理统计 第一章 概率论的基本概念 §1 随机试验 自然界和社会上发生的现象是多种 多样的,有一类现象为确定性现象: 在一定条件下必然发生的现象。 向空中抛一物体必然落向地面; 水加热到 100℃必然沸腾; 异性电荷相吸引; 放射性元素发生蜕变; . 还有一类为随机现象:在试验或 观察前无法预知出现什么结果。 抛一枚硬币结果可能正面(或反 面)朝上; 向同一目标射击,各次弹着点都 不相同; 某地区的日平均气温; 掷一颗骰子,可能出现的点数; . 统计规律性: 多次重复抛一枚硬币得到正面 朝上的结果大致有一半; 同一门大炮射击同一目标的着 弹点大致在目标附近且按照一 定的规律分布;

3.样本空间(S):随机试验E的所有可能结果 §2样本空间、随机事件 所组成的集合。样本空间的元素,即试验E的 每个结果,称为样本点(e)。 例2:给出EE,的样本空间 Su:(H,T): S2:(HHH,HHT,HTH,HTT,THH,THT, TTH,TTT): S3:(0,1,2,3 电话交换台一分钟内接到的呼 S4:(1,2,3,4,5,6; 唤次数的上限未知 S5:{0,1,2,3, 灯泡寿命上限未知 S6:(t≥0: x,y分别表示最低和最高温 S7:{(Ky川T,≤x≤y≤TJ。 度,T,和T分别表示该地区的 4.随机事件:试验E的样本空间S中满足某些 温度下限和上限。 条件的样本点所组成的集合,简称事件。 任何事件均可表示为样本空间的某个子集。 事件是样本空间的子集。在每 次试验中,当且仅当这一子集 由一个样本点组成的单点集称为基本事件, 中的一个样本点出现时,称这 两个特殊事件: 事件发生。 必然事件:样本空间S 不可能事件:空集 事件的表示:文字表述或样本空间的子集 例3: (1)E2:将一枚硬币连抛三次,考虑正反面 出现的情况: 事件A:“第一次出现的是H(正面)” (HHH,HHT,HTH,HTT) 事件B:“三次出现同一面”(HH,TTT) 事件C:“恰好出现一次正面” (HTT,THT,TTH)
3. 样本空间(S):随机试验 E 的所有可能结果 所组成的集合。样本空间的元素,即试验 E 的 每个结果,称为样本点(e)。 例2:给出 E1~E7的样本空间: S1:{H,T}; S2:{HHH,HHT,HTH,HTT,THH,THT, TTH,TTT}; S3:{0,1,2,3}; S4:{1,2,3,4,5,6}; S5:{0,1,2,3,.}; S6:{t| t 0 }; S7:{(x,y)| 0 T1 T x y }。 4. 随机事件:试验 E 的样本空间 S 中满足某些 条件的样本点所组成的集合,简称事件。 任何事件均可表示为样本空间的某个子集。 由一个样本点组成的单点集称为基本事件。 两个特殊事件: 必然事件:样本空间 S。 不可能事件:空集 。 事件的表示:文字表述或样本空间的子集。 例3: (1)E2: 将一枚硬币连抛三次,考虑正反面 出现的情况; 事件 A:“第一次出现的是 H(正面)” {HHH,HHT,HTH,HTT} 事件 B:“三次出现同一面” {HHH,TTT} 事件 C:“恰好出现一次正面” {HTT,THT,TTH} §2 样本空间、随机事件 电话交换台一分钟内接到的呼 唤次数的上限未知 灯泡寿命上限未知 x, y 分别表示最低和最高温 度, T0和T1 分别表示该地区的 温度下限和上限。 事件是样本空间的子集。在每 次试验中,当且仅当这一子集 中的一个样本点出现时,称这 一事件发生

(2)E6:在一批灯泡中任取一只,测试其寿 思考: 事件A与B是否会同时发生? 命 事件B与C是否会同时发生? 事件D1:“寿命小于1000小时” 为什么? {t0≤t≤1000]】 同一样本空间中,不同的事件 (3)E7:记录某地一昼夜的最高温度与最低 之间有一定的关系,如试验 当试验的结果是H 温度。 时,可以说事件A(至少出现 事件D2:“最高温度与最低温度相差10摄氏度” 个正面)和B(三次出现同 面)同时发生了:但事件B和 {(xy)y-x=10,T≤x≤y≤T} C(恰好出现一次正面)在任何 情况下均不可能同时发生。易 见,事件之间的关系是由他们 所包含的样本点所决定的,这 种关系可以用集合之间的关系 来描述。 (课间休息) 5.事件之间的关系 设试验E的样本空间为S,事件A,B, 4(k=1,2,3)是S的子集。 (1)包含关系:AcB 事件A发生必然导致事件B发生, 若A=B,则称事件A与事件B 若ACB且BCA,则A=B。 相等。 (2)和事件:AUB={xx∈A或xeB 事件AUB称为事件A与事件B 当且仅当事件A,B中至少有一个发生时,事的和事件。 件AUB发生, 类似地,称日A为n个事件4,4,A,的 和事件。 (3)积事件:AOB={x|x∈A且x∈B 事件A⌒B称为事件A与事件B 的积车件 当且仅当事件A,B同时发生时,事件A⌒B 发生,简记为AB。 类似地,称0A为n个事件4,A,.,An的
(2)E6: 在一批灯泡中任取一只,测试其寿 命; 事件 D1:“寿命小于 1000 小时” {t| 0 t 1000 } (3)E7: 记录某地一昼夜的最高温度与最低 温度 。 事件 D2:“最高温度与最低温度相差10摄氏度” {(x,y)|y-x=10, 0 T1 T x y } 思考: 事件 A与B 是否会同时发生? 事件 B 与C 是否会同时发生? 为什么? 同一样本空间中,不同的事件 之间有一定的关系,如试验 E2 ,当试验的结果是 HHH 时,可以说事件 A (至少出现一 个正面)和 B(三 次出现同一 面)同时发生了;但事件 B 和 C(恰好出现一次正面)在任何 情况下均不可能同时发生。易 见,事件之间的关系是由他们 所包含的样本点所决定的,这 种关系可以用集合之间的关系 来描述。 (课间休息) 5. 事件之间的关系 设试验 E 的样本空间为 S,事件 A,B, A (k = 1,2,3,.) k 是 S 的子集。 (1)包含关系: A B 事件 A 发生必然导致事件 B 发生。 若 A B 且 B A ,则 A = B 。 (2)和事件: AB ={x | x A或xB} 当且仅当事件 A,B 中至少有一个发生时,事 件 A B 发生。 类似地,称 k n k A =1 为 n 个事件 A A An , , , 1 2 的 和事件。 (3)积事件: AB ={x | x A且xB} 当且仅当事件 A,B 同时发生时,事件 A B 发生,简记为 AB。 类似地,称 k n k A =1 为 n 个事件 A A An , , , 1 2 的 若 A = B ,则称事件 A 与事件 B 相等。 事件 A B 称为事件 A 与事件 B 的和事件。 事件 A B 称为事件 A 与事件 B 的积事件

积事件。 (4)差事件:A-={xx∈A且rEB卧 事件AB称为事件A与事件B的 差事件。 当且仅当事件A发生、B不发生时,事件A-B 发生。 (5)互斥的或互不相容的事件:AnB= 基本事件是两两互不相容的。 事件A与事件B不能同时发生。 (6)逆事件或对立事件: 称事件A与事件B互为对立事件 或互为逆事件。 AUB=S阻AnB= 对每次试验而言,事件A、B中必有一个发 生,且仅有一个发生。 事件A的对立事件记为A,A=S-A。 6.事件的运算 设试验E的样本空间为S,事件A,B, A4(k=1,2,3)是S的子集。 (I)交换律:AUB=BUA,AnB=BnA (2)结合律: AU(BUC)=(AUB)UC A0(BOC)=(40B)OC (3)分配律: A(BOC)=(AUB)0(AUC) A0(ByC)=(A0BV(AOC) (4)德·摩根律: 推广: AUB=AnB,AnB=AUB 84=Q4,Q4=84
积事件。 (4)差事件:A-B= {x | x A且xB} 当且仅当事件 A 发生、B 不发生时,事件 A-B 发生。 (5)互斥的或互不相容的事件:A B = 事件 A 与事件 B 不能同时发生。 (6)逆事件或对立事件: AB = S且AB = 对每次试验而言,事件 A、B 中必有一个发 生,且仅有一个发生。 事件 A 的对立事件记为 A , A = S − A。 6. 事件的运算 设试验 E 的样本空间为 S,事件 A,B, A (k = 1,2,3,.) k 是 S 的子集。 (1)交换律:A B=B A,A B=B A (2)结合律: A (B C) = (A B) C A (B C) = (A B) C (3)分配律: A (B C) = (A B) (AC) A (B C) = (A B) (AC) (4)德 ∙ 摩根律: A B = A B , A B = A B 事件 A-B 称为事件 A 与事件 B 的 差事件。 基本事件是两两互不相容的。 称事件 A 与事件 B 互为对立事件 或互为逆事件。 k n k k n k k n k k n k A A A A =1 =1 =1 =1 = , = 推广: