
第七章 第,、节多元品数的极值及其求法 (Absolute maximum and minimum values) 一、多元函数的极值 二、条件极值拉格朗日乘数法 三、小结与思考练习 2009年7月6日星期一 目录 上页 下页 、返回
2009年7月6日星期一 1 目录 上页 下页 返回 第八节 多元函数的极值及其求法 第七章 (Absolute maximum and minimum values) 一、多元函数的极值 二、条件极值 拉格朗日乘数法 三、小结与思考练习

一、多元函数的极值及最大值、最小值 定义若函数z=f(x,y)在,点(x0,yo)的某邻域内有 f(x,y)≤f(xo,yo)(或f(x,y)≥f(xo,yo) 则称函数在该点取得极大值(极小值).极大值和极小值 统称为极值,使函数取得极值的点称为极值 例如: z=3x2+4y2在点(0,0)有极小值; z=-Vx2+y2在点(0,0)有极大值; z=xy在,点(0,0)无极值 2009年7月6日星期一 2 目录○ 上页) 下页 、返回
2009年7月6日星期一 2 目录 上页 下页 返回 x y z 一、 多元函数的极值及最大值、最小值 定义 若函数 则称函数在该点取得极大值 (极小值). 例如 : 在点 (0,0) 有极大值; 使函数取得极值的点称为极值点. 在点 (0,0) 有极小值; 在点 (0,0) 无极值. 极大值和极小值 统称为极值, ),(),( 00 f x y ≤ f x y )),(),(( 00 或 ≥ yxfyxf 22 += 43 yxz 2 2 z =− + x y z = x y ),(),( 00 = 在点 yxyxfz 的某邻域内有 x y z x y z

定理1(必要条件)函数z=f(x,y)在点(o,yo)存在 偏导数,且在该点取得极值,则有 f(x0,y0)=0,f(x0,y0)=0 证:因z=f(x,y)在点(xo,yo)取得极值,故 z=f(x,o)在x=x取得极值 2=∫(xo,y)在y=0取得极值 据一元函数极值的必要条件可知定理结论成立, 说明:使偏导数都为0的点称为驻,点 但驻,点不一定是极值点: 例如,z=xy有驻点(0,0),但在该点不取极值 2009年7月6日星期一 3 目录 上页 下页 、返回
2009年7月6日星期一 3 目录 上页 下页 返回 说明 : 使偏导数都为 0 的点称为驻点 . 例如 , 函数 偏导数, 证 : 据一元函数极值的必要条件可知定理结论成立. 0),(,0),( f x ′ x y00 = f y ′ x y00 = 取得极值 , 取得极值 取得极值 但驻点不一定是极值点. 有驻点( 0, 0 ), 但在该点不取极值. 且在该点取得极值 , 则有 ),(),( 00 = 在点 yxyxfz 存在 ),(),( 00 因 = 在点 yxyxfz = yxfz 0 ),( 在 0 x = x 故 = 0 yxfz ),( 在 0 y = y z = yx 定理1 (必要条件 )

定理2(充分条件)若函数z=f(x,y)在点(x0,y0)的 的某邻域内具有一阶和二阶连续偏导数,且 fx(x0,y0)=0,f(x0,0)=0 4A=fxx(xo,Yo),B=fxy(xo,Yo),C=fyy(xo,Yo) 「A0时,具有极值 A>0时取极小值 2)当AC-B2<0时,没有极值 3)当AC-B2=0时,不能确定,需另行讨论. 这个定理不加证明, 2009年7月6日星期一 4 目录 上页 下页 返回
2009年7月6日星期一 4 目录 上页 下页 返回 则: 1) 当 时, 具有极值 的某邻域内具有一阶和二阶连续偏导数, 且 令 A0 时取极小值. 2) 当 时, 没有极值. 3) 当 时, 不能确定 , 需另行讨论. 这个定理不加证明. 若函数 = 在点 yxyxfz 00 ),(),( 的 0),(,0),( f x x y00 = f y x y00 = ),(,),(,),( 00 00 00 A f x y B f x Cy f x y = xx = yx = yy 0 2 A C B >− 0 2 A C − B < 0 2 A C − B = 定理2 (充分条件 )

求函数?=f(x,y)极值的一般步骤: 第一步 解方程组f(x,y)=0,∫,(x,y)=0 求出实数解,得驻点 第二步 对于每一个驻点(X,y0), 求出二阶偏导数的值A、B、C 第三步定出AC-B的符号,再判定是否是极值 2009年7月6日星期一 5 目录 上页今 下页 、返回
2009年7月6日星期一 5 目录 上页 下页 返回 求函数 z = xf y),( 极值的一般步骤: 第一步 解方程组 yxf = ,0),( x yxf = 0),( y 求出实数解,得驻点. 第二步 对于每一个驻点 ),( 00 x y , 求出二阶偏导数的值 A 、 B 、 C. 第三步 定出 2 AC − B 的符号,再判定是否是极值

例1求函数f(x,y)=2xy-3x2-2y2+10的极值 (课本例4) 提示:第一步求驻点。 第二步判别。 A0时,具有极值 A>0时取极小值 2)当AC-B2<0时,没有极值 3)当AC-B2=0时,不能确定,需另行讨论, 2009年7月6日星期一 6 目录 上页 下页 返回
2009年7月6日星期一 6 目录 上页 下页 返回 例 1 求函数 2 2 f x y xy x y ( , ) 2 3 2 10 = −− + 的极值. (课本 例 4 ) 提示 : 第一步 求驻点. 第二步 判别. 1) 当 2 > 0 时, 具有极值 A0 时取极小值. 2) 当 3) 当 时, 没有极值. 时, 不能确定 , 需另行讨论. A C − B 0 2 A C − B < 0 2 A C − B =

例2求函数z=x2y(4-x-y)在直线x=0,y=0及 x+y=6所围成的三角形区域D上的最大值和最小值 (课本例5) 提示: 首先考察函数z在三角形区域D内的极值 其次,考察函数在三角形区域的边界上的最大值和 最小值. 2009年7月6日星期一 7 目录○ 上页下页 返回
2009年7月6日星期一 7 目录 上页 下页 返回 例 2 求函数 2 z = xy x y (4 ) − − 在直线 x = 0 , y = 0 及 x y + = 6 所围成的三角形区域 D 上的最大值和最小值. (课本 例 5 ) 提示 : 首先考察函数z在三角形区域D内的极值 其次,考察函数在三角形区域 的边界上的最大值和 最小值

说明: 从上例可以看出,计算函数x,y)在有界闭区域 D的边界上的最大值和最小值有时是相当复杂. 在通常遇到的实际问题中,根据问题的实际背 景往往可以断定函数的最大值与最小值一定在区域 D的内部取得,这时就可以不考虑函数在区域边界 上的取值情况了.如果又求得函数在区域内只有一 个驻点,那么则可直接断定该点处的函数值就是函 数在区域上的最大值或最小值, 2009年7月6日星期一 8 目录 上页 下页 、返回
2009年7月6日星期一 8 目录 上页 下页 返回 从上例可以看出,计算函数f(x, y )在有界闭区域 D的边界上的最大值和最小值有时是相当复杂. 在通常遇到的实际问题中,根据问题的实际背 景往往可以断定函数的最大值与最小值一定在区域 D的内部取得,这时就可以不考虑函数在区域边界 上的取值情况了.如果又求得函数在区域内只有一 个驻点,那么则可直接断定该点处的函数值就是函 数在区域上的最大值或最小值. 说明 :
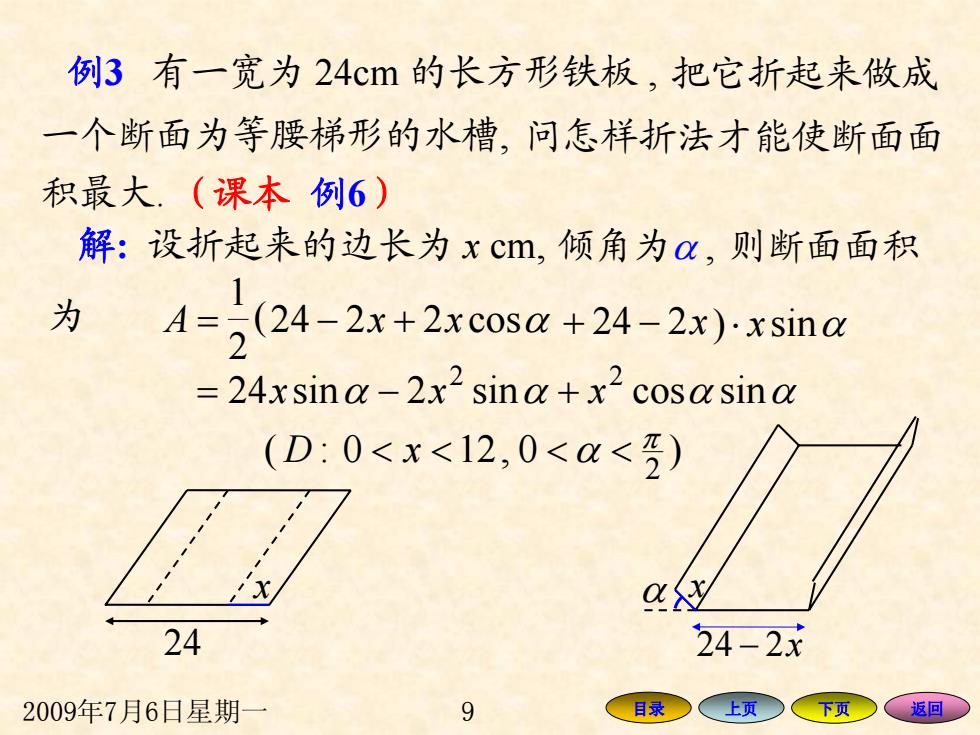
例3有一宽为24cm的长方形铁板,把它折起来做成 一个断面为等腰梯形的水槽,问怎样折法才能使断面面 积最大.(课本例6) 解:设折起来的边长为xcm,倾角为a,则断面面积 为 4=(24-2x+2xcosa +24-2x).xsina =24xsina-2x2 sina+x2 cosa sina (D:0<x<12,0<x<) 24 24-2X 2009年7月6日星期一 9 目录 上页 下页 、返回
2009年7月6日星期一 9 目录 上页 下页 返回 把它折起来做成 解 : 设折起来的边长为 x cm, 则断面面积 x 24 一个断面为等腰梯形的水槽, 倾角为 α , A = ( − x + x cos2224 α + − 224 x 2 1 ⋅ x sin) α α sin2sin24 α α sincos α 2 2 = − + xxx − 224 x α x 积最大. (课本 例 6 ) )0,120:( 2 π xD α <<<< 为 问怎样折法才能使断面面 例3 有一宽为 24cm 的长方形铁板

4=24xsina-2x2sina+x2 cosasina (D:0<x<12,0<a<) Ax =24sina-4xsina+2xsina cosa=0 令 A =24xcosa-2x2 cosa +x2(cos2 a-sin2a)=0 sina≠0,x≠0 12-2x+xC0sa=0 24cosa-2xcosa+x(cos2a-sin2a)=0 解得: 260,x=8(cm 由题意知,最大值在定义域D内达到,而在域D内只有 一个驻,点,故此,点即为所求. 2009年7月6日星期一 10 目录 上页 下页 返回
2009年7月6日星期一 10 目录 上页 下页 返回 x cos24 α cos2 α 2 − x (cos 0)sin 22 2 + x αα =− = 令 A x sin24 α − x sin4 α + x α α = 0cossin2 Aα = 解得: 由题意知,最大值在定义域D 内达到,而在域D 内只有 一个驻点, 故此点即为所求. α ≠ ,0sin x ≠ 0 α sin2sin24 α α sincos α 2 2 = − + xxxA )0,120:( 2 π xD α <<<< − + xx α = 0cos212 cos2cos24 (cos 0)sin22 αα xx αα =−+− (cm)8,60 3 x === π D α