
第六章 第四节空间曲孩及其方程 (Space Curve and Its Equations) 一、空间曲线的一般方程 二、空间曲线的参数方程 三、曲面的参数方程 四、空间曲线在坐标面上的投影 五、小结与思考练习 2009年7月3日星期五 目录 上页 下页 、返回
2009年7月3日星期五 1 目录 上页 下页 返回 第四节 空间曲线及其方程 第六章 (Space Curve and Its Equations) 四、空间曲线在坐标面上的投影 一、空间曲线的一般方程 二、空间曲线的参数方程 三、曲面的参数方程 五、小结与思考练习

一、空间曲线的一般方程 (General Equation of Space Curve) 空间曲线可视为两曲面的交线,其一般方程为方程组 F(x,y,z)=0 S2 S G(x,y,z)=0 0 G(x,y,z)= F(x,y2)=0 例如,方程组 x2+y2=1 2x+3z=6 表示圆柱面与平面的交线C 2009年7月3日星期五 2 目录○ 、上页 下页 返回
2009年7月3日星期五 2 目录 上页 下页 返回 一、空间曲线的一般方程 空间曲线可视为两曲面的交线, 其一般方程为方程组 ⎩ ⎨ ⎧ = = ( , , ) 0 ( , , ) 0 G x y z F x y z 2 S L G ( x, y,z ) = 0 F ( x, y,z ) = 0 1 S 例如,方程组 ⎩ ⎨ ⎧ + = + = 2 3 6 1 2 2 x z x y 表示圆柱面与平面的交线 C. x z 1 y o C 2 (General Equation of Space Curve)
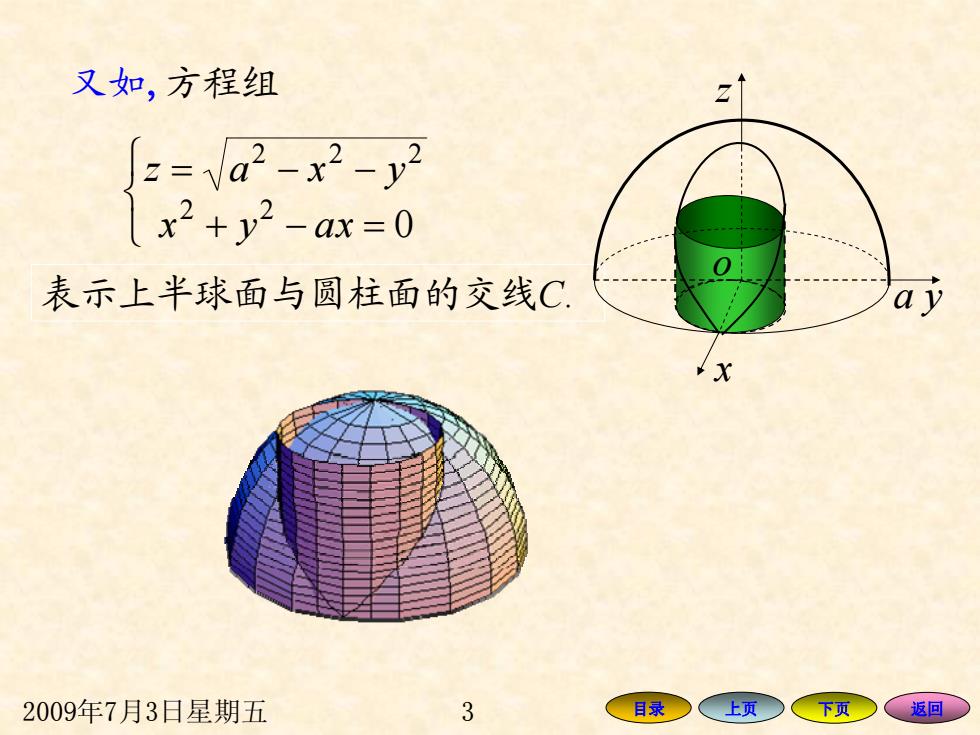
又如,方程组 2 表示上半球面与圆柱面的交线C ay 2009年7月3日星期五 3 目录○ 上页下页 (返回
2009年7月3日星期五 3 目录 上页 下页 返回 表示上半球面与圆柱面的交线 C. ⎩ ⎨ ⎧ =−+ −−= 0 22 222 xayx yxaz y x z a o 又如 ,方程组

二、空间曲线的参数方程 (The Parametric Equation of Space Curve) 将曲线C上的动,点坐标x,y,z表示成参数t的函数: x=x(t) y=y(t) 称它为空间曲线的 参数方程. 2=z(t) 例如,圆柱螺旋线的参数方程为 x=acosot y=asinot令0=ot,b=y x=acose Z=vt y=asine z=b0 当0=2π时,上升高度h=2πb,称为螺距 2009年7月3日星期五 4 目录○ 上页 下页 返回
2009年7月3日星期五 4 目录 上页 下页 返回 二、空间曲线的参数方程 将曲线 C上的动点坐标x, y, z表示成参数 t 的函数: z x y o )( 称它为空间曲线的 参数方程. = xx t 例如,圆柱螺旋线 ω ωθ v 令 , bt == θ θ θ z b ay ax = = = sin cos 当 θ = π 时,2 h = 2π b x = a cos ω t y = asin ω t z = v t 的参数方程为 上升高度 , 称为螺距 . y = y t)( z = z t)( θ M (The Parametric Equation of Space Curve)

例1(补充题)将下列曲线化为参数方程表示: (1) x2+y2=1 z=va2-x2-y2 2x+3z=6 2+y2-ax=0 解:(1)根据第一方程引入参数,得所求为 x=coSt y=sint (0≤t≤2π) (z=3(6-2c0st) (②)将第二方程变形为(Gx-)2+y2=,故所求为 rx=号+号cost y=gsint (0≤t≤2π) (=av-cost 2009年7月3日星期五 5 目录 上页 下页 、返回
2009年7月3日星期五 5 目录 上页 下页 返回 ⎩ ⎨ ⎧ =+ =+ 632 1 )1( 22 zx yx ⎩ ⎨ ⎧ =−+ −−= 0 )2( 22 222 xayx yxaz 解 : (1) 根据第一方程引入参数 , x = cos t y = sin t )cos26( 3 1 z = − t (2) 将第二方程变形为 )( , 4 22 2 2 a a yx =+− 故所求为 得所求为 x t aa cos 22 = + ty a sin 2 = costaz 2 1 2 1 −= ≤ t ≤ π )20( ≤ t ≤ π )20( 例 1(补充题)将下列曲线化为参数方程表示:

三、曲面的参数方程 (The Parametric Equation of Surface) 一般曲面的参数方程含两个参数,形如 x=x(s,t) y=y(s,t) z=(s,t) 2009年7月3日星期五 6 目录 、上页下页 返回○
2009年7月3日星期五 6 目录 上页 下页 返回 三、曲面的参数方程 (The Parametric Equation of Surface) 一般曲面的参数方程含两个参数 , 形如 = xx s t),( y = y s t),( z = z s t),(

x=p(t) 例2求空间曲线「: y=v(t) (a≤t≤B)绕z轴旋转 z=0(t) 时的旋转曲面方程 解:任取点M1(p(t),w(t),o(t)∈「,点M,绕z轴旋转, 转过角度0后到点M(x,y,),则 「x=√p2()+w2()c0s0 (asisB y=Vo2()+w2(0)sn0 0≤0≤2π z=0(t) 这就是旋转曲面满足的参数方程 2009年7月3日星期五 7 目录 (上页 下页 、返回
2009年7月3日星期五 7 目录 上页 下页 返回 x = ϕ t)( y = ψ t)( z = ω t)( α ≤ t ≤ β )( 绕 z 轴旋转 时的旋转曲面方程 . 解 : ,))(,)(,)(( 任取点 1 ϕ ψ ω tttM ∈ Γ 点 M1 绕 z 轴旋转, 转过角度 θ 后到点 M x y z ,),( 则 cos)()( θψϕ2 2 += ttx sin)()( θψϕ2 2 += tty z = ω t)( ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ≤≤ ≤ ≤ πθ α β 20 t 这就是旋转曲面满足的参数方程 . 例2 求空间曲线 Γ:

x=1 例如,直线 y=t绕z轴旋转所得旋转曲面方程为 z=2t x=1+12cos0 y=v1+t2 sing /o0<t<+0 0≤0≤2π z=2t 消去t和0,得旋转曲面方程为 4(x2+y2)-z2=4 2009年7月3日星期五 8 目录 、上页 (下页 、返回
2009年7月3日星期五 8 目录 上页 下页 返回 x = 1 y = t z = 2 t 绕 z 轴旋转所得旋转曲面方程为 cos1 θ 2 += tx sin1 θ 2 += ty z = 2 t ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ≤≤ − <∞ < + ∞ 20 πθ t 消去 t 和 θ , 得旋转曲面方程为 4)(4 222 zyx =−+ x z o y 例如 , 直线

x=asino 又如,x0z面上的半圆周y=0 (0≤p≤π) z=acoso 绕z轴旋转所得旋转曲面(即球面)方程为 x=asin p cosθ y=asino sin 0≤p≤π 0≤0≤2π z=acoso 2009年7月3日星期五 9 目录 上页今 下页 、返回
2009年7月3日星期五 9 目录 上页 下页 返回 绕 z 轴旋转所得旋转曲面 ( 即球面 ) 方程为 x = asin ϕ y = 0 z = a cos ϕ x = a ϕ cossin θ y = a ϕ sinsin θ z = a cos ϕ ≤ ϕ ≤ π )0( ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ≤≤ ≤ ≤ πθ ϕ π 20 0 又如 , xoz 面上的半圆周

四、空间曲线在坐标面上的投影 (Projecting Curve on a Coordinate Plane of Space Curve) 设空间曲线C的一般方程为 F(x,y,2)=0 G(x,y,z)=0 消去z得投影柱面H(x,y)=0, 2 则C在xOy面上的投影曲线C'为 H(x,y)=0 z=0 消去x得C在y0z面上的投影曲线方程 R(y,z)=0 x=0 消去y得C在zox面上的投影曲线方程 T(x,z)=0 y=0 2009年7月3日星期五 10 目录 上页 下页 返回
2009年7月3日星期五 10 目录 上页 下页 返回 四、空间曲线在坐标面上的投影 设空间曲线 C 的一般方程为 消去 z 得投影柱面 消去 x 得C 在yoz 面上的投影曲线方程 消去y 得C 在zox 面上的投影曲线方程 ⎩ ⎨ ⎧ = 则C 在xoy 面上的投影曲线 C´为 = 0),( 0),( zyxG zyxF H x y = ,0),( (, ) 0 0 Hxy z ⎧ = ⎨ ⎩ = (,) 0 0 Ryz x ⎧ = ⎨ ⎩ = (,) 0 0 Txz y ⎧ = ⎨ ⎩ = z y x C C′ (Projecting Curve on a Coordinate Plane of Space Curve)