
第三章 第七节曲车(Curvature) 一、孤微分 二、曲率及其计算公式 三、曲率半径与曲率圆 四、小结与思考练习 2009年7月3日星期五 1 目录 上页 下 、返回
2009年7月3日星期五 1 目录 上页 下页 返回 第七节 曲 率 第三章 二、曲率及其计算公式 (Curvature) 四、小结与思考练习 三、曲率半径与曲率圆 一、弧微分

一、孤微分Element of Length or Differential of Arc 设函数y=f(x)在区间 (a,b)内具有连续的导数, 在曲线y=f(x)上取固定点 M A(x,y)作为度量孤长的基点 对曲线上任一点M(x,y),规定: (1)依x增大的方向作为曲线的正向. (2)M=5,当有句孤段1的方向与曲线的正向 一致时s>0,相反时s<0: 显然,s=s(x)是是x的单调增加函数 2009年7月3日星期五 2 目录 上页 返回
2009年7月3日星期五 2 目录 上页 下页 返回 一、弧微分( Element of Length or Differential of Arc ) A 0 x M x x y o 设函数 y fx = ( ) 在区间 (,) a b 内具有连续的导数, 在曲线 y f = ( ) x 上 取固定 点 0 0 A(, ) x y 作为度量弧长的基点 对曲线上任一点 M (, ) x y ,规定: (1)依 x 增大的方向作为曲线的正向. (2) q AM s = ,当有向弧段 q AM 的方向与曲线的正向 一致时 s >0,相反时s <0. 显然, s = s x( )是是 x 的单调增加函数.
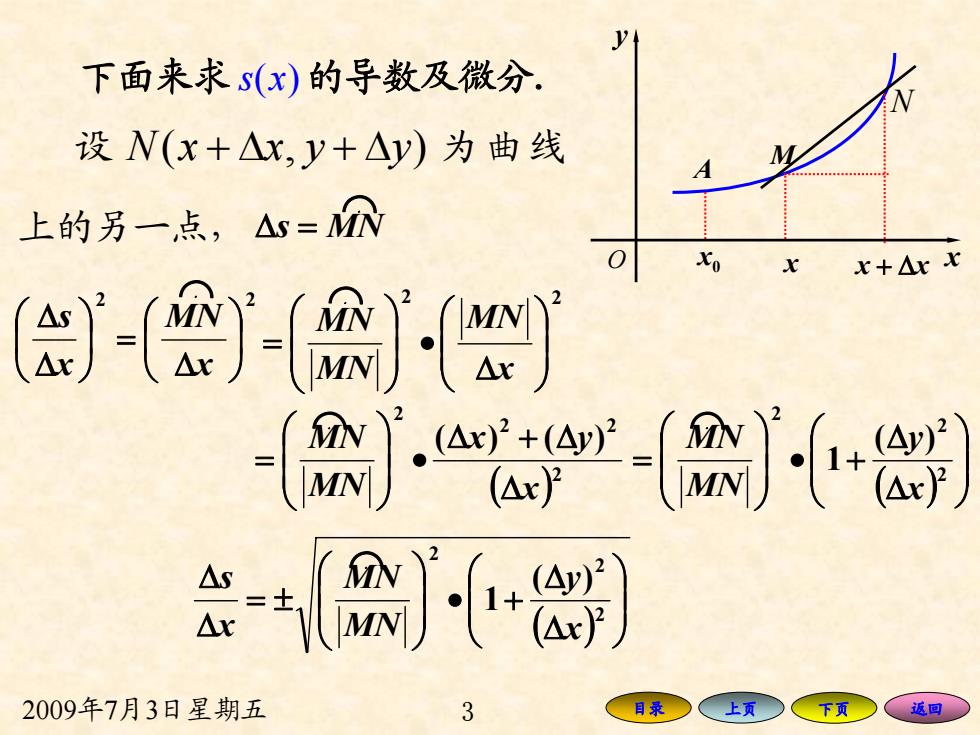
下面来求s(x)的导数及微分. 设N(x+△x,y+△y)为曲线 上的另一点,△= x+△x (-(】 -等+ 如-中】 2009年7月3日星期五 3 目录 上页 返回
2009年7月3日星期五 3 目录 上页 下页 返回 下面来求 s( ) x 的导数及微分. 设 Nx xy y (, ) +Δ +Δ 为曲线 上的另一点, A 0 x M x x y O N + Δxx Δ = MNs j 2 2 ⎟⎠⎞ ⎜⎝⎛ Δ ⎟ = ⎠⎞ ⎜⎝⎛ ΔΔ x MN xs j 2 2 ⎟⎟⎠⎞ ⎜⎜⎝⎛ Δ • ⎟⎟⎠⎞ ⎜⎜⎝⎛ = x MN MN MNj ( )2 2 2 2 )()( x yx MN MN Δ Δ+Δ • ⎟⎟⎠⎞ ⎜⎜⎝⎛ = j ( ) ⎟⎟⎠⎞ ⎜⎜⎝⎛ ΔΔ +• ⎟⎟⎠⎞ ⎜⎜⎝⎛ = 22 2 )( 1 xy MN MN j ( ) ⎟⎟⎠⎞ ⎜⎜⎝⎛ ΔΔ +• ⎟⎟⎠⎞ ⎜⎜⎝⎛ ±= ΔΔ 22 2 )( 1 xy MN MN xs j
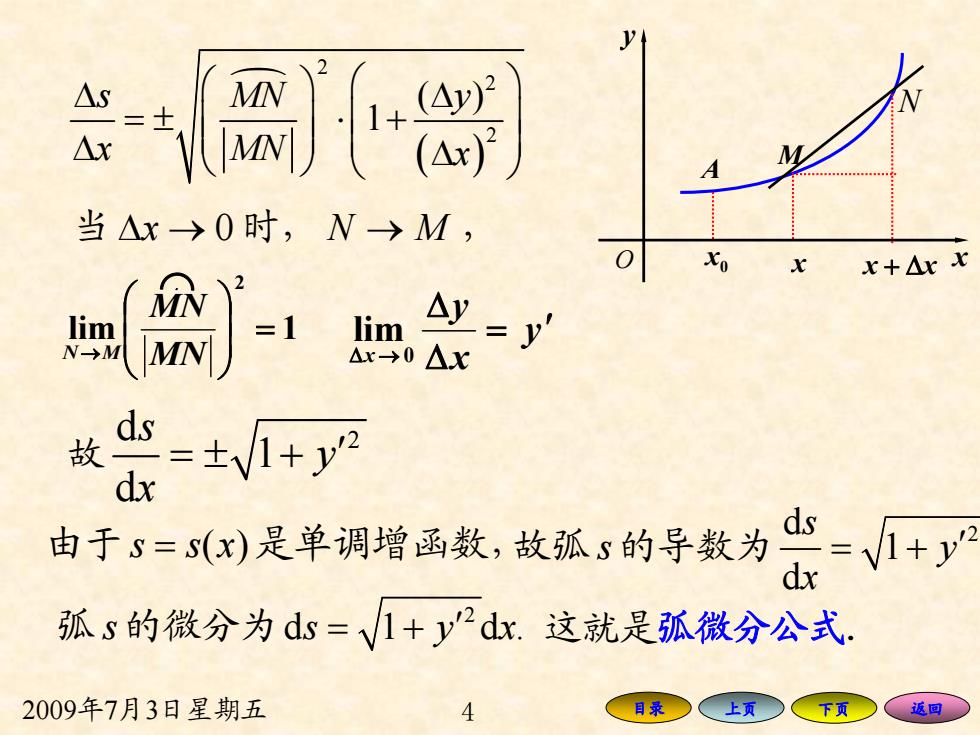
当△x→0时,N→M, x+△xx N lim Ay=y' Ax→0△X 故s=±+y dx 由于s=()是单调增函数,故孤的导数为 =1+y x 孤s的微分为ds=V1+ydx.这就是弧微分公式 2009年7月3日星期五 4 目录 上页 返回
2009年7月3日星期五 4 目录 上页 下页 返回 q ( ) 2 2 2 ( ) 1 s MN y x MN x Δ Δ ⎛ ⎞ ⎛ ⎞ =± ⋅ + ⎜ ⎟ ⎜ ⎟ Δ ⎜ ⎟ ⎝ ⎠ ⎜ ⎟ Δ ⎝ ⎠ A 0 x M x x y O N + Δxx 当 Δx → 0 时, N M → , lim 1 2 = ⎟⎟⎠⎞ ⎜⎜⎝⎛ → MN MN MN j y xy x = ′ ΔΔ →Δ 0 lim 故 d 2 1 d s y x =± + ′ 由于 s = s x( )是单调增函数,故弧 s 的导数为 d 2 1 ds y x = + ′ 弧 s 的微分为 2 d 1 d. s y = + ′ x 这就是弧微分公式.

二、曲率及其计算公式(Curvature and Formula) 1曲率的定义 -描述曲线局部性质(弯曲程度)的量。 Aa. △S M M 1)孤段弯曲程度越大转角越大, 2)转角相同孤段越短弯曲程度越大。 2009年7月3日星期五 5 目录 上页 返回
2009年7月3日星期五 5 目录 上页 下页 返回 二、曲率及其计算公式 (Curvature and Formula) -描述曲线局部性质(弯曲程度)的量。 M1 M3 )Δα2 M2 ΔS2 ΔS1 M M′ ΔS1 ΔS2 N N′ )Δα 1)弧段弯曲程度越大转角越大, αΔ 1 ) 2)转角相同弧段越短弯曲程度越大。 1 曲率的定义
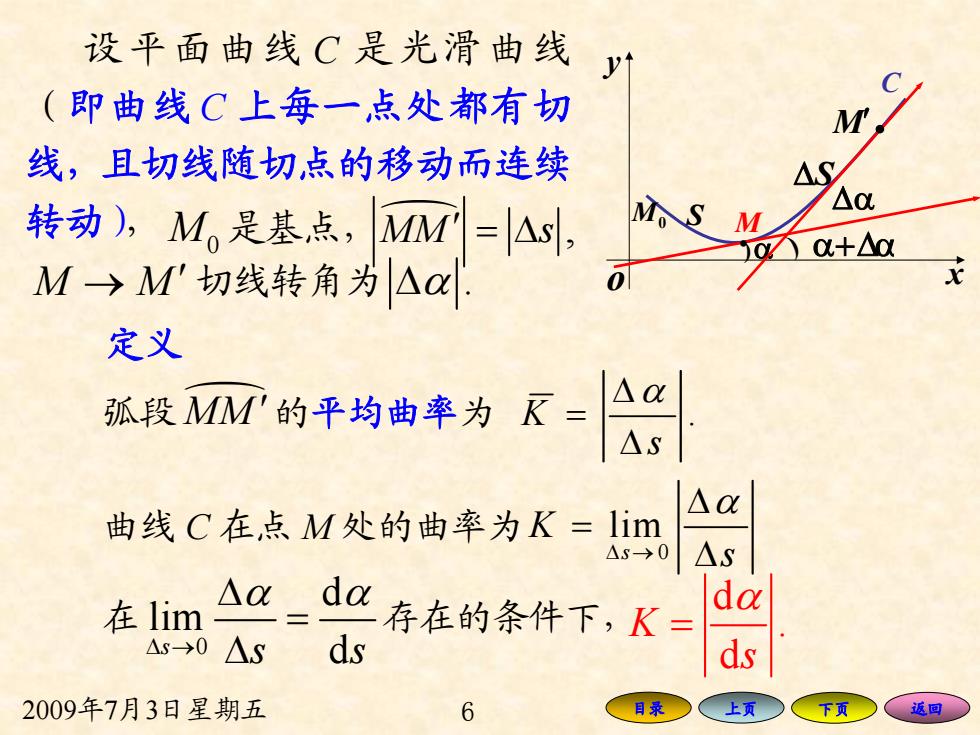
设平面曲线C是光滑曲线 y (即曲线C上每一点处都有切 线,且切线随切点的移动而连续 转动,M,是基点,MM=As, 价SM △0 0+△ M→M'切线转角为△ 定义 弧收预的华均商率为双A △O 曲线C在点M处的曲率为K=lim △S→0 △S △ 在lim 义=dC存在的条件下,K da △s-→0△S ds ds 2009年7月3日星期五 6 目录 上页 返回
2009年7月3日星期五 6 目录 上页 下页 返回 设平面曲线 C 是光滑曲线 (即曲线 C 上每一点处都有切 线,且切线随切点的移动而连续 转动), y o x M C M0 M0 是基点, )α. M′. S ΔS M q M s ′ = Δ , M → M ′ 切线转角为 Δα . ) α+Δα Δα 定义 弧段M q M ′的平均曲率为 K . s Δα = Δ 曲线 C 在点 M 处的曲率为 0 lim s K s α Δ → Δ = Δ 在 0 d lim s s sd α α Δ → Δ = Δ 存在的条件下, d . d K sα =

例如,直线的曲率处处为零 事实上,△x=0,K= 又如,圆上各,点处的曲率等于半径的倒数,且半径越 小曲率越大 事实上, 设圆的半径为“,则由弧长、圆心角和半径的关系有 4a= △S 即4a 1 △S 故K= 2009年7月3日星期五 7 上页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 事实上,Δ = α 0, 例如,直线的曲率处处为零. K 0 s Δα = = Δ 又如, 圆上各点处的曲率等于半径的倒数,且半径越 小曲率越大. 事实上, 设圆的半径为r ,则由弧长、圆心角和半径的关系有 s r α Δ Δ = 即 1 s r Δα = Δ 故 1 K s r Δα = = Δ

2曲率的计算公式 设曲线的方程为y=f(x),且f(x)具有二阶导数, 由tan=y',有a=arctany'.从而 da =y” dx 1+y2 即d女十dx.另一方面,由弧分公式细 ds=V1+ydx.得曲率计算公式为K= da 若曲线由参数方程二给出,则曲率计算公式为 y=w(t) k-"-p"w( [020+w(0]月 2009年7月3日星期五 8 目录 上页 、返回
2009 年 7 月 3日星期五 8 目录 上页 下页 返回 2 曲率的计算公式 设曲线的方程为 y fx = ( ) ,且 f x( ) 具有二阶导数. 由 tan α = y′ ,有 α = arctan . y′ 从而 2 d d 1 y x y α ′′ = + ′ . 即 2 d 1 d y x y α ′′ = + ′ . 另一方面,由弧微分公式知, 2 d s = +1 y x ′ d .得曲率计算公式为 d d K s α = 3 2 2 . (1 ) y y ′′ = + ′ 若曲线由参数方程 ( ), ( ) x t y t ϕ ψ ⎧ = ⎨ ⎩ = 给出,则曲率计算公式为 3 2 2 2 () () () () . () () tt tt K t t ϕψ ϕψ ϕ ψ ′ ′′ ′′ ′ − = ⎡ ⎤ ′ ′ + ⎣ ⎦

例1求抛物线y=ax2+bx+c上任意一,点处的曲率, 并问那一点的曲率最大? 解:易知,y=2ax+b,y”=2a,由曲率计算公式知, K= y 2a 0+1+(2ax+b}]月 因为当x= b时,K有最大值2a, 2a 而X= 所对应的点为抛物线的顶点, 2a 因此,抛物线在顶点处的曲率最大 2009年7月3日星期五 9 日录 上页 返回
2009年7月3日星期五 9 目录 上页 下页 返回 例 1 求抛物线 2 y ax bx c = + + 上任意一点处的曲率, 并问那一点的曲率最大? 解:易知, y ax b ′ = 2 + , y a ′′ = 2 ,由曲率计算公式知, 3 2 2 (1 ) y K y ′′ = + ′ ( ) 3 2 2 2 1 2 a ax b + = ⎡ + ⎤ ⎣ ⎦ 因为当 2 b x a = − 时,K 有最大值 2a , 而 2 b x a = − 所对应的点为抛物线的顶点, 因此,抛物线在顶点处的曲率最大.

例2求摆线 〔x=at-sn以在t=处的曲率 y=a(1-cost) 2 解:因为 少 sint dy 1 dx 1-cost dx2 a(1-c0st)2 所以由曲率计算公式知, k =-ly"l 1 3 (1+y2)2 2v2av1-cost 2009年7月3日星期五 10 目录 上页 返回
2009年7月3日星期五 10 目录 上页 下页 返回 例 2 求摆线 ( sin ), (1 cos ) x at t ya t ⎧ = − ⎨⎩ = − 在 π2 t = 处的曲率. 解: 因为 sin d 1 co d s y x t t = − , 2 2 2 1 . (1 cos d d ) y x a t = − − 所以由曲率计算公式知, 3 2 2 (1 ) y K y ′′ = + ′ 1 2 2 1 cos a t = − 令 π , 2 t = 得 π2 24 t K a = = .