
第三章 第二节泰勃公式(Taylor Formula) 理论分析 用多项式近似表示函数一应用 近似计算 一、泰勒公式的建立 二、几个初等函数的麦克劳林公式 三、泰勒公式的应用 四、小结与思考练习 2009年7月3日星期五 1 日录 上页 返回
2009年7月3日星期五 1 目录 上页 下页 返回 第二节 泰勒公式 第三章 (Taylor Formula) 用多项式近似表示函数 — 应用 理论分析 近似计算 二、几个初等函数的麦克劳林公式 一、泰勒公式的建立 三、泰勒公式的应用 四、小结与思考练习
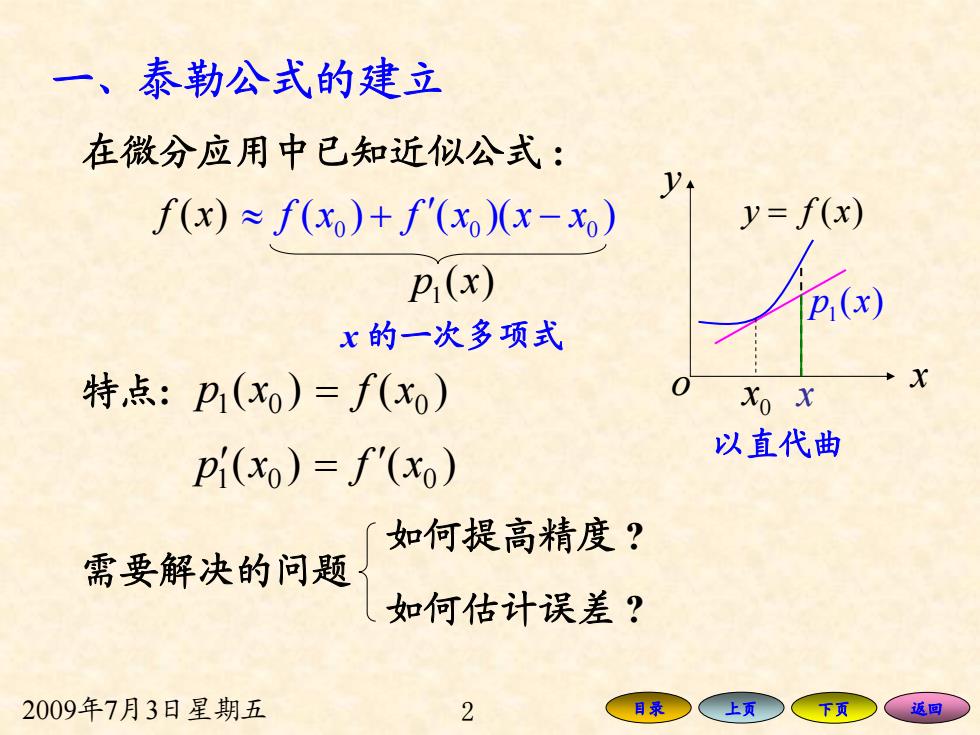
一、泰勒公式的建立 在微分应用中已知近似公式: f(x)≈f(x)+f'(xx-x) y=f(x) P(x) P(x) x的一次多项式 特点:p(xo)=f(xo) X Xo x 以直代曲 pi(xo)=f(xo) 如何提高精度? 需要解决的问题 如何估计误差? 2009年7月3日星期五 2 目录 上页 、返回
2009年7月3日星期五 2 目录 上页 下页 返回 一、泰勒公式的建立 特点: )( 01′ xp )( 0 = xf )( 0 = ′ xf xf )( x y = xfy )( o 0 00 ≈+ − f ( ) ( )( ) x fx xx ′ )(1 xp 以直代曲 0 x )(1 xp )( 01 xp 在微分应用中已知近似公式 : 需要解决的问题 如何提高精度 ? 如何估计误差 ? x x 的一次多项式

1.求n次近似多项式pn(x),并要求它的系数满足: Pa(xo)=f(xo).P(xo)=f(xo).(xo)=f((xo) 令pn(x)=a+a(x-x)+a2(x-x)2+.+an(x-) 则 Pi(x)= 4+2a2(x-x0)++nan(x-x)n- ph(x)= 2la2++n(n-1)an(x-x0)n-2 。 p (x)= nlan ao=Pn(xo)=f(xo), 41=p,(xo)=f'(xo), 4=p(x0)=分f"(o),.,an=ap"(xo)=fm(x) 故P()=f(x)+/八(xx-)+2f"(xx-)2+. (o)x-) + 2009年7月3日星期五 目录 上页 返回
2009年7月3日星期五 3 目录 上页 下页 返回 并要求它的系数满足: p x ,)( n )( !2 0 1 2 xpa n = ′′ ,)( 0 = f ′′ x ", )( 0 )( !1 xpa n n = n n )( 0 )( xf n = n xp )( = 0 故 f ( ) x 0 0 + f x ′( )( ) x x − +" !2 1 ! 1 n ) 0 ( 0 ( )( ) n n + − f x x x 1n! 0 2 0 + − f ′′( ) x ( ) x x 1 2! 令 n xp )( = 则 n′ xp )( = n ′′ xp )( = """" )( = )( xp nn n !an )( 0 0xpa = n ,)( 0 = f x ,)()( 00xp f x n = )( 01 xpa n = ′ ,)( 0 = f ′ x 1a )(2 02 + − xxa 1 0 )( − −++ n n " xxan 2 !2 a 2 0 )()1( − −−++ n n " xxann ,)()( 0 0 xp f x n′ = ′ )()(, 0 )( 0 )( xfxp n n " n = 0 a 1 0 0 2 2 0 ( )( ) ( ) n n + − + − ++ − a a xx xx " a x x 1. 求 n 次近似多项式

2.余项估计 令R(x)=f(x)-Pn(x)(称为余项),则有 R(xo)=Ri(o)=.=Ro (xo)=0 R,(x) (x-xo) R(x)-R,(%o) R,(51) (51在x0与x之间) (x-x)”1-0 (n+1)(51-x)” R(51)-R,(xo) P(52) (52在x0与 (n+10(5-xo)”_-0(n+1)(52-x)-1 51之间) R(5n)-Rm()_R+(5) (5在x0与x之间) (n+1).2(5n-xo)-0(n+1)川 2009年7月3日星期五 目录 上页 返回
2009年7月3日星期五 4 目录 上页 下页 返回 ) 0 (ξ x 与在 ξ n 之间 )( )( 1 0 + − = n n xx R x )(2)1( )( 0 )( n x R n n n n −+ = ξ ξ " () () () Rn n 令 x fx p x = − (称为余项) , )( 0 R x n )( 0 R x n = ′ 0)( 0 )( xR === n " n 1 0 ( ) ( ) n n R x x x + − n n xn R ))(1( )( 01 1 −+ ′ = ξ ξ ))(1( )( 01 1 n n xn R −+ ′ = ξ ξ 1 02 2 )()1( )( − −+ ′′ = n n xnn R ξ ξ =" ( 1) ( ) ( 1) ! n R n n ξ + = + 则有 0 ( ) Rn − x −0 0 ( ) Rn − ′ x −0 ( ) 0 ( ) n −R x n −0 x ) 01 (ξ x 与在 x 之间 ) 1 02 ( 之间 与在 ξ ξ x 2. 余项估计

R(x)=f(x)-pn(x) R(x) Rm+(5) (5在x0与x之间) (n+1)川 p()=0,RmD(x)=f(D(x) R)(x-x,产 (n+1)川 (5在x0与x之间) 当在x的某邻域内f+(x)≤M时 R国nn-“ .R(x)=o(x-xo)”)(x→x) 2009年7月3日星期五 6 目录 上页 返回
2009年7月3日星期五 5 目录 上页 下页 返回 R x f x p x)()()( n = − n 1 0 )( )( + − n n xx R x !)1( )()1( + = + n R nn ξ ) 0 (ξ x 与在 x 之间 ,0)()1( = + xp n ∵ n ( 1) 1 0 ( ) () ( ) ( 1) ! n n n f Rx x x n ξ + + = − + )()()1( )1( xfxR n n n + + ∴ = 当在 x0 的某邻域内 n+ )1( )( ≤ Mxf 时 ) 0 (ξ x 与在 x 之间 1 0 !)1( )( + − + ≤ n n xx nM xR )())(()( 0 0 xxxxoxR n ∴ n −= →

泰勒中值定理: 若f(x)在包含xo的某开区间(a,b)内具有 直到n+1阶的导数,则当x∈(a,b)时,有 f0x)=f)+f0x-)+o)(x-x+ 2! +f0(o(x-o)P+R,( ① n! 共中R侧=0白x-)y"(传在,与x之同@ (n+1)月 公式①称为f(x)的n阶泰勒公式. 公式②称为n阶泰勒公式的拉格朗日余项. 2009年7月3日星期五 6 上页 、返回
2009年7月3日星期五 6 目录 上页 下页 返回 公式 ① 称为 的xf )( n 阶泰勒公式 . 若 )( 在包含 xxf 0的某开区间 ba ),( 内具有 直到n +1阶的导数 , bax ),( 公式 ② 称为n 阶泰勒公式的拉格朗日余项 . ∈ 时, 有 f x)( = )( 0 f x ))(( 0 0 + f ′ − xxx 2 0 0 )( !2 )( xx f x − ′′ + +" n n xx n xf )( ! )( 0 0 )( + − ( ) Rn + x ① 其中 ( 1) 1 0 ( ) () ( ) ( 1) ! n n n f Rx x x n ξ + + = − + 则当 ) 0 (ξ 与在 xx 之间 ② 泰勒中值定理 :

注意到R(x)=o(x-x)”] ③ 在不需要余项的精确表达式时,泰勒公式可写为 f)=f)+f(x-0+3(x-x)}+. 21 +m((x-)”+ox-x)"] ④ nl 公式③称为n阶泰勒公式的佩亚诺Peano)余项. *可以证明: f(x)在,点x有直到n阶的导数 ④式成立 2009年7月3日星期五 上页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 公式 ③ 称为n 阶泰勒公式的佩亚诺(Peano) 余项 . f x)( = f x0 )( + f ′ 0 − xxx 0 ))(( 0 0 )( 2+" !2 )( xx f x − ′′ + n n xx n xf )( ! )( 0 0 )( + − ])[( 0 n −+ xxo ④ 0 ( ) [( ) ] n 注意到 Rx ox x n = − ③ * 可以证明: )( 在点 0 有直到nxxf 阶的导数 ④ 式成立 在不需要余项的精确表达式时 , 泰勒公式可写为

0=f)+/X-)+3(-6}+ 21 +mx-x,”+但(x-x) (n+1)川 特例: (5在x0与x之间) (1)当n=0时,泰勒公式给出拉格朗日中值定理 f(x)=f(x)+f'(5)(x-x) (5在x0与x之间) (2)当n=1时,泰勒公式变为 f)=f()+f(Xx-x)+-s 可见f(x)≈f(x)+f'(xx-xo) 2老在x0与x之间) 误差1 国-x-户(E在x,与x之) df 2009年7月3日星期五 8 目录 上页 、返回
2009年7月3日星期五 8 目录 上页 下页 返回 f ( ) x = )( 0 f x ))(( 0 0 + f ′ − xxx +" ( 1) 1 0 ( ) ( ) ( 1) ! n n f x x n ξ + + + − + 2 0 0 )( !2 )( xx f x − ′′ + n n xx n xf )( ! )( 0 0 )( + − ) 0 (ξ 与在 xx 之间 特例: (1) 当 n = 0 时, 泰勒公式变为 f ( ) x = 0 f ( ) x 0 + f ′( )( ) ξ x x − (2) 当 n = 1 时, 泰勒公式变为 给出拉格朗日中值定理 f ( ) x = 0 f x( ) 0 0 + f ′( )( ) x xx − 2 0 ( ) ( ) 2 ! f x x ′′ ξ + − 可见 f x)( ≈ )( 0 f x ))(( 0 0 + f ′ − xxx 2 1 0 )( !2 )( )( xx f xR − ′′ = ξ 误差 d f ) 0 (ξ 与在 xx 之间 ) 0 (ξ 与在 xx 之间 ) 0 (ξ 与在 xx 之间

在泰勒公式中若取x=0,5=0x(0<0<1),则有 f)=f0+f0x+0x2+.+0x 2 n! +f》(0)xml (n+1)! 称为麦克劳林(Maclaurin)公式. 由此得近似公式 fx)≈f0)+f'0x+0x+.+f0x 2 n! 若在公式成立的区间上fm(x)≤M,则有误差估计式 Rwmm M 2009年7月3日星期五 9 目录○ 上页
2009 年 7 月 3日星期五 9 目录 上页 下页 返回 称为麦克劳林( Maclaurin )公式 . 0 x x = 0 , (0 1) , ξ = << θ θ x)( = 则有 f f )0( + f ′ )0( x + " 1 )1( !)1( )( + + + + n n x n θ xf 2 !2 )0( x f ′′ + n n x n f ! )0()( + f x)( = )( 0 f x ))(( 0 0 + f ′ − xxx + " 1 0 )1( )( !)1( )( + + − + + n n xx n f ξ 2 0 0 )( !2 )( xx f x − ′′ + n n xx n xf )( ! )( 0 0 )( + − ) 0 (ξ 与在 xx 之间 f ( ) x ≈ f (0) + f ′(0) x + " ( 1) () , n f x M + ≤ 则有误差估计式 1 !)1( )( + + ≤ n n x n M xR 2 !2 )0( x f ′′ + n n x n f ! )0()( + 若在公式成立的区间上 由此得近似公式 在泰勒公式中若取

二、几个初等函数的麦克劳林公式 (1)f(x)=ex fk(x)=e,f(0)=1(k=1,2,) .e*=1+x 2* n1+R,() 其中Rn(x)= n+01x1 (0<8<1) 2009年7月3日星期五 10 目录 上页 、返回
2009年7月3日星期五 10 目录 上页 下页 返回 二、几个初等函数的麦克劳林公式 x )()1( = exf ,)( k )( x ∵ = exf ),2,1(1)0( f k )( k == " x ∴ e =1 + x !3 3 x + +" n ! x n + R x)( + n !2 2 x + 其中 Rn x)( = n + !)1( <θ < )10( n+1 x x eθ