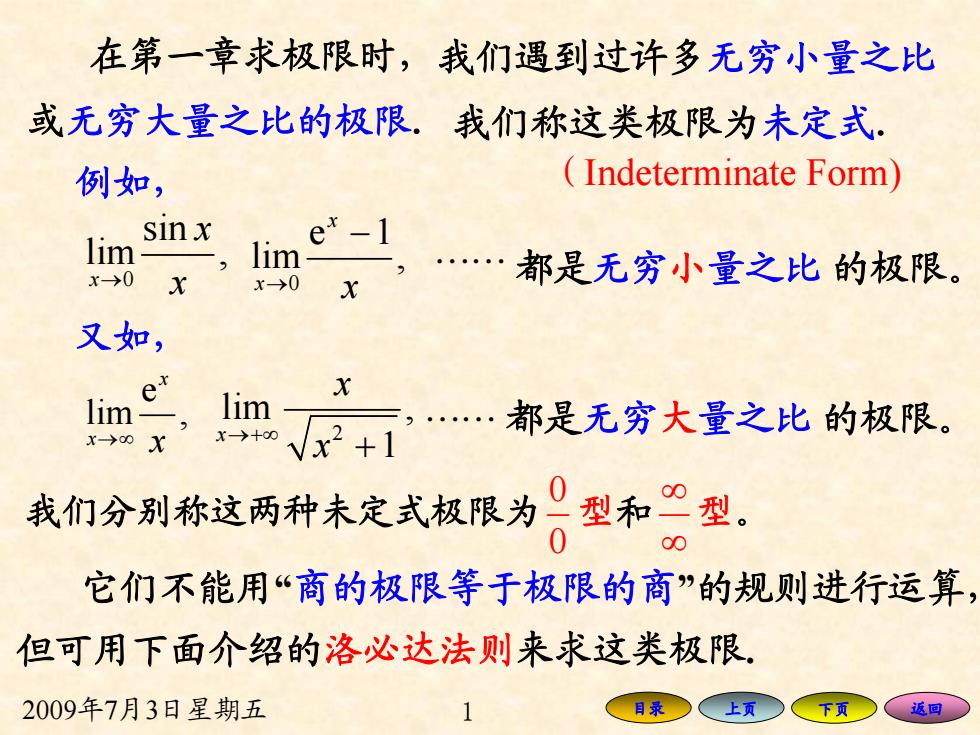
在第一章求极限时,我们遇到过许多无穷小量之比 或无穷大量之比的极限.我们称这类极限为未定式, 例如, Indeterminate Form) inx lim- e*-1 x→0 , x→0 .都是无穷小量之比的极限。 又如, lim ”十.都是无穷大量之比的板限。 lim x-→0X 我们分别称这两种未定式极限为。型和”型。 它们不能用“商的极限等于极限的商”的规则进行运算, 但可用下面介绍的洛必达法则来求这类极限, 2009年7月3日星期五 目录 上页 返回
2009年7月3日星期五 1 目录 上页 下页 返回 在第一章求极限时,我们遇到过许多无穷小量之比 或无穷大量之比的极限.我们称这类极限为未定式. 例如, (Indeterminate Form) 0 sin lim , x x → x 0 e 1 lim , x x→ x − "" 都是无穷小量之比 的极限。 又如, e lim , x x→∞ x 2 lim , 1 x xx →+∞ + "" 都是无穷大量之比 的极限。 我们分别称这两种未定式极限为 00 型和 ∞∞ 型。 它们不能用“商的极限等于极限的商”的规则进行运算, 但可用下面介绍的洛必达法则来求这类极限

第三章 第三节洛必达法则 (L'Hospital's Rule) 0 一、 型未定式的洛必达法则 二、0 型未定式的洛必达法则 00 三、其他类型的未定式 四、小结与思考练习 2009年7月3日星期五 2 目录○ 上页 下 、返回
2009年7月3日星期五 2 目录 上页 下页 返回 第三节 洛必达法则 第三章 (L’Hospital’s Rule) 三、其他类型的未定式 二、 ∞ ∞ 型未定式的洛必达法则 一、 型未定式的洛必达法则 00 四、小结与思考练习

型未定式洛必达法则 0 定理1 1)lim f(x)=lim F(x)=0 x→a x→a 2)f(x)与F(x)在U(a)内可导,且F'(x)≠0 3)lim f'(x) 存在(或为0) xa F(x) lim f(x) lim f'(x) (洛必达法则) a F(x) 3a F(x) 2009年7月3日星期五 3 目录○ 上页 返回
2009年7月3日星期五 3 目录 上页 下页 返回 一、 型未定式洛必达法则 = = 0)(lim)(lim)1 → → f xFx ax ax )( )( lim)3 xFf x ax ′′ → 存在 (或为∞ ) () () lim lim () () xa xa f x fx → → F x Fx ′ = ′ 在与 axFxf 内可导,)()()()2 D ∪ 且F′ x ≠ 0)( 定理 1 0 0 (洛必达法则)

定理条件:1)limf(x)=limF(x)=0 x→a x→a 2)f(x)与F(x)在U(a)内可导,且F'(x)≠0 3)lim I'(x) xa F'(x) 存在(或为0)》 证:无妨假设f(=F(a)=0,在指出的邻域内任取 x≠a,则f(x),F(x)在以飞,a为端点的区间上满足柯 西定理条件,故 f(x)-f(x)-f(a四_f'(5) (5在x,a之间) F(x)F(x)-F(a)F'(5) 13) lim ( x→aF(x) x→aF'(5) x→aF'(x) 2009年7月3日星期五 4 上页 返回
2009年7月3日星期五 4 目录 上页 下页 返回 ( ξ 在 x , a 之间) 无妨假设 f = aFa = ,0)()( 在指出的邻域内任取 ≠ ax , 则 f xFx )(,)( 在以 x, a 为端点的区间上满足柯 = = 0)(lim)(lim)1 → → f xFx ax ax 故 )()( )()( )( )( aFxF f x f a xF f x − − = )( )( ξ ξ F f ′ ′ = )( )( lim xF f x →ax ∴ )( )( lim ξ ξ F f ax ′ ′ = → )( )( lim xF f x ax ′ ′ → )3 定理条件: 西定理条件, )( )( lim)3 xFf x ax ′′ → 存在 (或为∞ ) 在与 axFxf 内可导,)()()()2 D ∪ 且 ′ xF ≠ 0)( 证:

洛必达法则 lim f(x) lim f'(x) F(x) xa F'(x) 推论1定理1中x→a换为 x→a,x>4,x→0,x→+0,x→-o0 之一,条件2)作相应的修改,定理1仍然成立. 推论2若1m得5品梨且w.F满灵定 F'(x) 理1条件,则 lim=lim=lim) F(x) -"F'(x) F"(x) 2009年7月3日星期五 5 目录 上页 、返回
2009年7月3日星期五 5 目录 上页 下页 返回 定理 1 中 → ax , 换为 → + ax , → − ax x ∞→ , x −∞→ 之一, 推论 2 若 )( )( lim xFf x ′′ 仍属 且型 )(,)(, 满足定 00 ′′ xFxf 理1条件, 则 )( )( lim )( )( lim xF f x xF f x ′ ′ = )( )( lim xF f x ′′ ′′ = 条件 2) 作相应的修改 , 定理 1 仍然成立. x +∞→ , )( )( lim )( )( lim xF f x xF f x ax ax ′ ′ = → → 洛必达法则 推论1

x3-3x+2 0 -2-x+1 例1求lim 型 0 解:原式=lim 3x2-3 x13x2-2x-1 6x ,3 li 、 x16x-22 注意:不是未定式不能用洛必达法则! 6x 6 li x-16x-2 ≠lim6=l x→>16 2009年7月3日星期五 6 目录○ 上页 下 返回
2009年7月3日星期五 6 目录 上页 下页 返回 . 1 23 lim 23 3 1 − − + +− → xxx xx x 解: 原式 lim →1 = x 0 0 型 26 6 lim 1 − = → x x x 2 3 = 注意: 不是未定式不能用洛必达法则 ! 26 6 lim →1 x − x x 1 6 6 lim 1 = x→ ≠ 33 2 x − 123 2 xx −− 例1 求
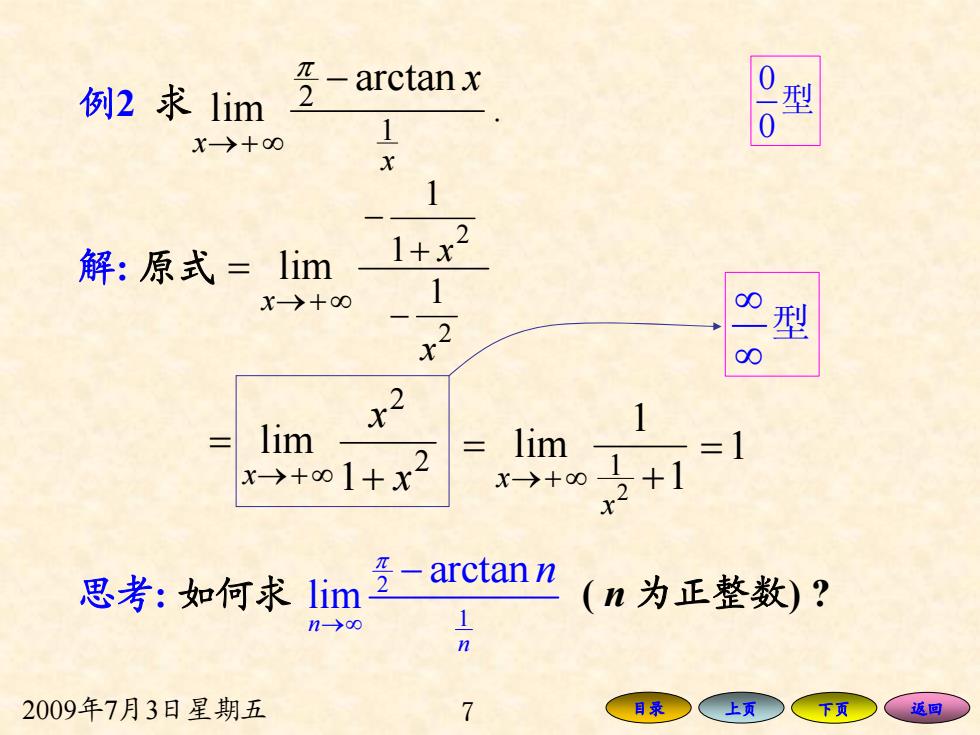
例2求lim 3-6 arctan x 型 0 X>+00 1 1 解:原式=lim 1+x X>十0∞ 1 00 2 型 00 x2 1 lim lim X+01+x2 =I >+∞21 思考:如何求lim 号-arctann (n为正整数)? n-→o0 1 n 2009年7月3日星期五 7 目录 上页 、返回
2009年7月3日星期五 7 目录 上页 下页 返回 . arctan lim 1 2 x x − x ∞+→ π 解: 原式 lim ∞+→ = x 0 0 型 2 2 1 lim x x x + = ∞+→ =1 2 1 1 + x − 2 1 x − 1 1 lim 2 1 + = ∞+→ x x 思考: 如何求 2 1 arctan limn n n π →∞ − ( n 为正整数) ? ∞ ∞ 型 例2 求

二、”型未定式的洛必达法则 00 定理2. 1)limf(x)=limF(x)=o X→a 2)f(x)与F(x)在U(a)内可导,且F'(x)≠0 3)1im四存在(或为) x→aF'(x) lim '(x) (洛必达法则) x→aF(x) xa F(x) (证明略) 2009年7月3日星期五 8 日录 上页 返回
2009年7月3日星期五 8 目录 上页 下页 返回 二、 型未定式的洛必达法则 ∞ ∞ 1) lim ( ) lim ( ) xa xa f x Fx → → = = ∞ )( )( lim)3 xFf x ax ′′ → 存在 (或为∞) ( ) lim ( ) x a f x → F x 定理 2. (证明略) ( ) lim ( ) x a f x → F x ′ = ′ (洛必达法则) 在与 axFxf 内可导,)()()()2 D ∪ 且F′ x ≠ 0)(

说明:定理中x→a换为 x→a, X→a,x→0, x→十0, X〉-0 之一,条件2)作相应的修改,定理仍然成立 2009年7月3日星期五 9 目录 上页( 下顶 返回
2009年7月3日星期五 9 目录 上页 下页 返回 说明: 定理中 → ax 换为 之一, 条件 2) 作相应的修改 , 定理仍然成立. , → + ax , → − ax x → ∞, x +∞→ , x −∞→

例3求lim Inx (n>0). 型 K-→+0xn 00 1 解:原式=lim 1 x→+oorn-=lim =0 x-→+o0nxn 例4求m灯D0,2 00 型 00 解:(1)n为正整数的情形. 原式=lim nx-1 Aehx lim (n-1)xn-2 x→+00 x-→+00 Reix n! == lim =0 x-→too2ex 2009年7月3日星期五 10 目录○ 上页 返回
2009 年 7 月 3日星期五 10 目录 上页 下页 返回 .)0( ln lim > +∞→ n x x n x 解 : ∞ ∞ 型 原式 1 1 lim − +∞→ = n x x xn n x xn 1 lim +∞→ = = 0 例 4 求 解 : (1) n 为正整数的情形 . 原式 = 0 x n x e xn λ λ 1 lim − +∞→ = x n x e xnn λ λ 2 2 )1( lim − +∞→ − = xn x e n λ λ ! lim +∞→ "== >> .)0, 0(lim +∞→ λ λ n e x x n x ∞ ∞ 型 例3 求