
第五章 第五节定积分的元素法及其应用 Element Method of Definite Integral and Its Applications 一、定积分的元素法 二、定积分在几何学上的应用 三、定积分在物理学上的应用 四、思考与练习 2009年7月3日星期五 1 目录○ 上页 下页 返回
2009年7月3日星期五 1 目录 上页 下页 返回 第五节 定积分的元素法及其应用 第五章 (Element Method of Definite Integral and Its Applications ) 二、定积分在几何学上的应用 一、定积分的元素法 三、定积分在物理学上的应用 四、思考与练习

一、定积分的元素法 1.什么问题可以用定积分解决? 1)所求量U是与区间[a,b]上的某分布f(x)有关的 一个整体量; 2)U对区间[a,b]具有可加性,即可通过 “大化小,常代变,近似和,取极限” 表示为U=lim∑f(5)△x, 1→0-1 定积分定义 fx)dx=lm∑f5)Ax 20 2009年7月3日星期五 目录 (上页 下页 、返回
2009年7月3日星期五 2 目录 上页 下页 返回 一、定积分的元素法 1. 什么问题可以用定积分解决 ? 表示为 ∑ → = = Δ n i ii U xf 1 0 ξ )(limλ 1) 所求量 U 是与区间 [ a , b ]上的某分布 f (x ) 有关的 2) U 对区间 [ a , b ] 具有可加性 , 即可通过 “大化小, 常代变, 近似和, 取极限 ” ∫ b a d)( xxf ∑ → = = Δ n i ii xf 1 0 ξ )(limλ 定积分定义 一个整体量 ;

2.如何应用定积分解决问题? 第一步利用化整为零,以常代变”求出局部量的 近似值 微分表达式 dU=f(x)dx 第二步利用“积零为整,无限累加”求出整体量的 精确值 积分表达式 U=∫fx)dx 这种分析方法成为元素法(或微元分析法) 元素的几何形状常取为:条,带,段,环扇,片,壳等 2009年7月3日星期五 3 目录 上页 下页 返回
2009年7月3日星期五 3 目录 上页 下页 返回 第一步 利用 “化整为零 , 以常代变 ” 求出局部量的 微分表达式 U = f d)(d xx 第二步 利用 “ 积零为整 , 无限累加 ” 求出整体量的 积分表达式 U = xxf b a d)( ∫ 这种分析方法成为元素法 ( 或微元分析法 ) 元素的几何形状常取为: 条, 带, 段, 环, 扇, 片, 壳 等 近似值 精确值 2. 如何应用定积分解决问题 ?

二、定积分在几何学上的应用 1.平面图形的面积 若函数f(x)、g(x)在[a,]上连续,且f(x)≥g(x), 则由曲线y=f(x)、y=g(x)及直线x=a、x=b所围 成的平面图形的面积为A=∫[f(,)-g()dx 其中面积A的元素为dA=[f(x)-g(x)]dx. 类似地,若函数p(y)、w(y)在[c,d]上连续,且 (y)≥W(y),则由曲线x=p(y)、x=w(y)及直线y=c、 y=d所围成的平面图形的面积为A=∫[py)-(y)dy 其中面积A的元素为dA=[p(y)-(y)]dy. 2009年7月3日星期五 4 目录 上页 下页 、返回
2009年7月3日星期五 4 目录 上页 下页 返回 二、定积分在几何学上的应用 1. 平面图形的面积 若函数 f ( ) x 、 g( ) x 在[,] a b 上连续, 且 f () () x ≥ g x , 则由曲线 y f = ( ) x 、 y g = ( ) x 及直线 x = a 、 x = b 所围 成的平面图形的面积为 [ ] () () d b a A = f x gx − x ∫ 其中面积 A 的元素为d () ()d A f x gx x = − [ ] . 类似地,若函数 ϕ( ) y 、 ψ ( ) y 在[, ] c d 上连续,且 ϕ() () y y ≥ ψ ,则由曲线 x = ϕ( ) y 、 x = ψ ( ) y 及直线 y c = 、 y = d 所围成的平面图形的面积为 [ ] () () d d c A = ϕ ψ y y − y ∫ 其中面积 A 的元素为d ( ) ( )d A y yy = − [ϕ ψ ] .
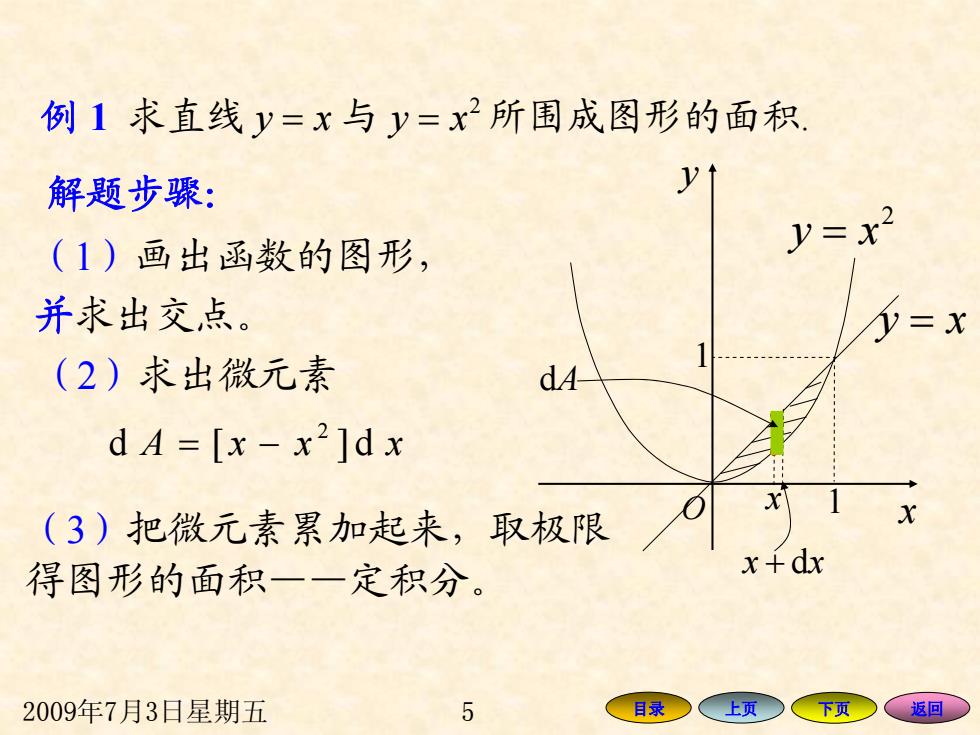
例1求直线y=x与y=x2所围成图形的面积 解题步骤: y (1)画出函数的图形, y=x2 并求出交点。 V=X (2)求出微元素 d4 dA=[x-x2]dx (3)把微元素累加起来,取极限 得图形的面积一一定积分。 x+dx 2009年7月3日星期五 5 目录○ 人上页 下页 、返回
2009年7月3日星期五 5 目录 上页 下页 返回 例 1 求直线 y x = 与 2 y x = 所围成图形的面积. O x y 1 1 2 y = x y = x 解题步骤: ( 1 )画出函数的图形, 并求出交点。 ( 2 )求出微元素 x x + dx 2 d [ ]d A xx x = − ( 3 )把微元素累加起来,取极限 得图形的面积——定积分。 dA

例2求抛物线y2=2x与直线x-y=4所围成的图 形的面积 解题步骤: (1)画出函数的图形,并求出交点。 (2)求出微元素 (3)把微元素累加起来,取极限得图形的面积一一 定积分。 2009年7月3日星期五 6 目录○ 上页下页 返回
2009年7月3日星期五 6 目录 上页 下页 返回 例 2 求抛物线 2 y x = 2 与直线 x y − = 4 所围成的图 形的面积. 解题步骤: ( 1 )画出函数的图形, 并求出交点。 ( 2 )求出微元素 ( 3 )把微元素累加起来,取极限得图形的面积—— 定积分

例3求椭圆 户1所围图形的面积 解:利用对称性,有dA=ydx 4-4ydx 利用椭圆的参数方程 ox x+dxa x x=acost y=bsint (0≤t≤2π) 应用定积分换元法得 bsin(asin)b sin2d =4ah~2号=ab 当a=b时得圆面积公式 2009年7月3日星期五 7 目录 上页 下页 返回
2009年7月3日星期五 7 目录 上页 下页 返回 a b o x y x 1 2 2 2 2 =+ b y a x 解 : 利用对称性 , A = y dd x 所围图形的面积 . 有 ∫ = a xyA 0 d4 利用椭圆的参数方程 )20( sin cos ≤≤ π ⎩ ⎨ ⎧ = = t tby ax t 应用定积分换元法得 ∫ = 0 2 4 π A bsin t ⋅ − a t d)sin( t ∫ = 2 0 2 dsin4 π ttba = 4 ba 2 1⋅ 2 π ⋅ = π ba 当 a = b 时得圆面积公式 x + d x 例3 求椭圆

设p(0)∈C[C,B],p(0)≥0,求由曲线r=p(0)及 射线B=α,0=B围成的曲边扇形的面积 在区间[a,B]上任取小区间[0,0+d0] 则对应该小区间上曲边扇形面积的近似值为 d-jlod0 (θ 所求曲边扇形的面积为 A-ON X 2009年7月3日星期五 8 目录 上页 下页 返回
2009年7月3日星期五 8 目录 上页 下页 返回 设 ϕ θ ∈ C α β ϕ θ ≥ ,0)(,],[)( 求由曲线 r = ϕ θ )( 及 射线 θ = α ,θ = β 围成的曲边扇形的面积 . r = ϕ θ )( α x θ d θ 在区间 α β ],[ 上任取小区间 θ ,[ θ + d θ ] 则对应该小区间上曲边扇形面积的近似值为 [ ] d)( θθϕ 2 1 d 2 A = 所求曲边扇形的面积为 θθϕ β α d)( 2 1 2 ∫ A = β
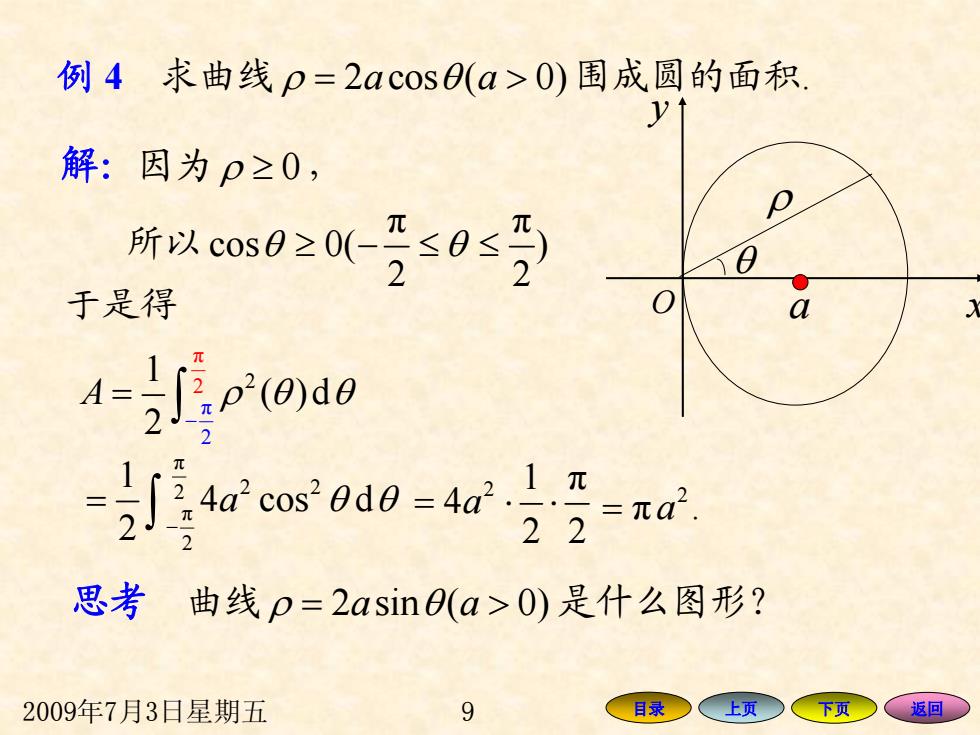
例4求曲线p=2acos0(a>0)围成圆的面积, 解:因为p≥0, 所以cms0≥0(-经s0s孕 于是 A-S.Od0 =星4acos0d0=4n.1a 22 =元a2 思考曲线p=2asin0(a>0)是什么图形? 2009年7月3日星期五 9 目录 上页 下页 返回
2009年7月3日星期五 9 目录 上页 下页 返回 例 4 求曲线 ρ = 2 cos ( 0) a a θ > 围成圆的面积. O x y a ρ θ 解:因为 ρ ≥ 0, 所以 π π cos 0( ) 2 2 θ θ ≥−≤≤ 于是得 π 2 π 1 2 2 ( )d 2 A ρ θ θ − = ∫ π 2 2 2 π 2 1 4 cos d 2 a θ θ − = ∫ 2 1 π 4 2 2 = a ⋅ ⋅ 2 = π a . 思考 曲线 ρ = 2 sin ( 0) a a θ > 是什么图形?
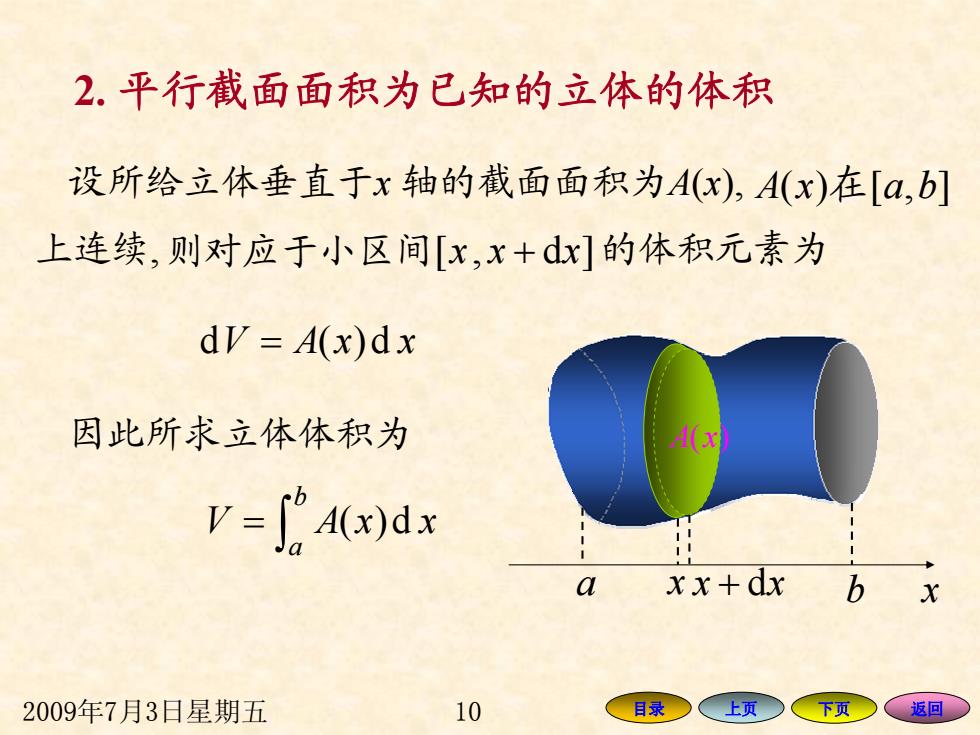
2.平行截面面积为已知的立体的体积 设所给立体垂直于x轴的截面面积为A(x),A(x)在[a,b] 上连续,则对应于小区间[x,x+dx]的体积元素为 dV=A(x)dx 因此所求立体体积为 V=)dx a xx+dx 2009年7月3日星期五 10 目录 (上页 下页 、返回
2009年7月3日星期五 10 目录 上页 下页 返回 设所给立体垂直于 x 轴的截面面积为 A (x), 在 baxA ],[)( 则对应于小区间 + xxx ]d,[ 的体积元素为 V = d)(d xxA 因此所求立体体积为 xxAV b a d)( ∫ = a x + dxx b x A( ) x 上连续, 2. 平行截面面积为已知的立体的体积