
第七章多元岛数微今法及其应用 一元函数微分学 推广 多元函数微分学 注意:善于类比,区别异同 2009年7月5日星期日 2 目录○ 上页 下页 返回
2009年7月5日星期日 2 目录 上页 下页 返回 第七章 多元函数微分法及其应用 推广 一元函数微分学 多元函数微分学 注意 : 善于类比, 区别异同

主要为容 第一节多元函数的基本概念 第二节 偏导数 第三节 全微分 第四节 多元复合函数的求导法则 第五节 隐函数的求导公式 第六节 多元微分学在几何上的应用 第七节 方向导数与梯度 第八节 多元函数的极值及其求法 2009年7月5日星期日 3 目录 上页 下页 、返回
2009年7月5日星期日 3 目录 上页 下页 返回 主要内容 第一节 多元函数的基本概念 第二节 偏导数 第三节 全微分 第四节 多元复合函数的求导法则 第五节 隐函数的求导公式 第六节 多元微分学在几何上的应用 第七节 方向导数与梯度 第八节 多元函数的极值及其求法

第七章 第一节多元函数的基本概念 (Conception of functions of several variables) 一、平面点集n维空间 二、多元函数的概念 三、多元函数的极限 四、多元函数的连续性 五、小结与思考练习 2009年7月5日星期日 4 目录 上页 下页 返回
2009年7月5日星期日 4 目录 上页 下页 返回 第一节 多元函数的基本概念 第七章 (Conception of functions of several variables) 四、多元函数的连续性 一、平面点集 n 维空间 二、多元函数的概念 三、多元函数的极限 五、小结与思考练习

一、平面,点集n维空间 1.邻域 点集U(6,δ)={PPPo<δ,称为点Po的6邻域, 例如,在平面上, U(,δ)=《xy)V(x-x)2+(y-o)2<δ(圆邻域) 在空间中, U(,)=《x,yzN(x-x)2+0y-0)2+(e-0)2<δ} (球邻域) 说明:若不需要强调邻域半径δ,也可写成U() 点Po的去心邻域记为U(P)={P0<PR<δ} 2009年7月5日星期日 5 目录 上页 下页 返回
2009年7月5日星期日 5 目录 上页 下页 返回 0 )( { } o U = PP 0 δ < PP0 < 一、平面点集 n 维空间 1. 邻域 点集 ,( δ { }, ) 0 = PPU 称为点 P0 的 δ 邻域. 例如 ,在平面上, 0 ,( δ = { yxPU ),() }(圆邻域) 在空间中, 0 δ = { zyxPU ),(),( } (球邻域) 说明:若不需要强调邻域半径 δ ,也可写成 .)( U P0 点 P 0 的去心邻域记为 δ PP0 < )()( δ 2 0 2 0 yyxx <−+− )()()( δ 2 0 2 0 2 0 zzyyxx <−+−+−

在讨论实际问题中也常使用方邻域,因为方邻域与圆 邻域可以互相包含: 平面上的方邻域为 U(,6)={(x,ylx-x (下页 、返回
2009年7月5日星期日 6 目录 上页 下页 返回 在讨论实际问题中也常使用方邻域, 平面上的方邻域为 UP xy ( , ) ( , ) 0 δ = { } . P0 因为方邻域与圆 邻域可以互相包含. 0 x x − < δ , 0 y y − < δ
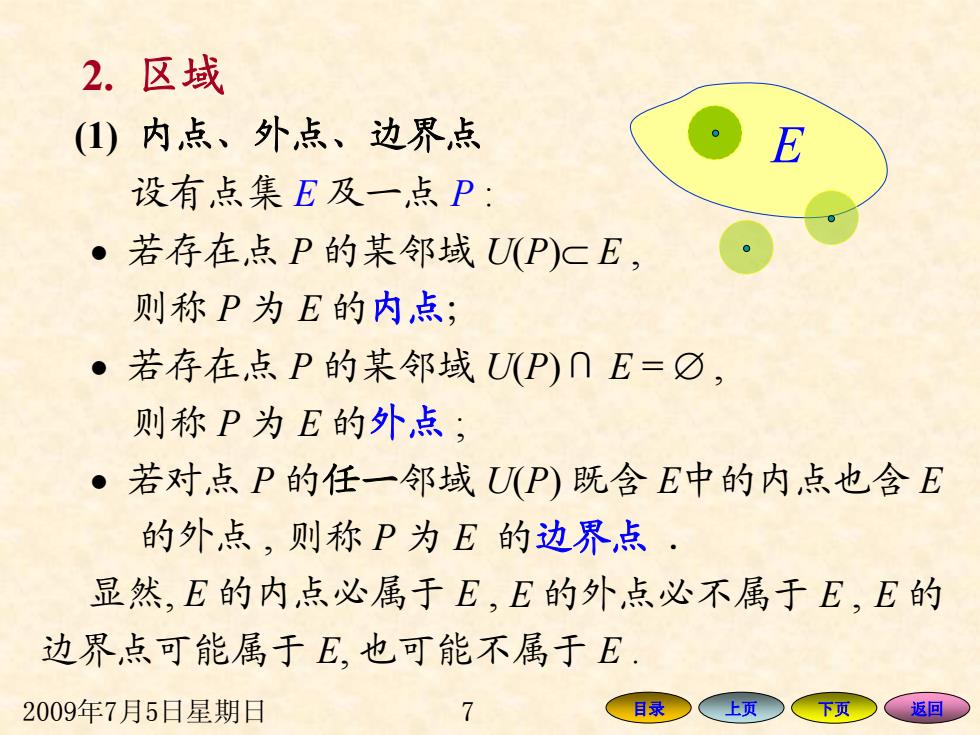
2.区域 ()内点、外点、边界点 E 设有点集E及一点P: ·若存在,点P的某邻域U(P)cE, 则称P为E的内点; ●若存在,点P的某邻域U(P)∩E=☑, 则称P为E的外点; ·若对点P的任一邻域U(P)既含E中的内点也含E 的外点,则称P为E的边界点· 显然,E的内点必属于E,E的外点必不属于E,E的 边界,点可能属于E,也可能不属于E 2009年7月5日星期日 7 目录 上页今下页 返回
2009年7月5日星期日 7 目录 上页 下页 返回 (1) 内点、外点、边界点 设有点集 E 及一点 P : • 若存在点 P 的某邻域 U(P ) ⊂ E , • 若存在点 P 的某邻域 U(P ) ∩ E = ∅ , • 若对点 P 的任一邻域 U( P) 既含 E中的内点也含 E E 则称 P 为 E 的内点; 则称 P 为 E 的外点 ; 的外点 , 则称 P 为 E 的边界点 . 显然, E 的内点必属于 E , E 的外点必不属于 E , E 的 边界点可能属于 E, 也可能不属于 E . 2. 区域

(2)聚点 若对任意给定的δ,点P的去心 E 邻域U(P,δ)内总有E中的点,则 称P是E的聚点. 聚点可以属于E,也可以不属于E(因为聚点可以为 E的边界点) 所有聚点所成的点集成为E的导集 2009年7月5日星期日 8 目录○ 。上页 下页 、返回
2009年7月5日星期日 8 目录 上页 下页 返回 若对任意给定的 δ , 点 P 的去心 U P,( δ ) D E 邻域 内总有 E 中的点 , 则 称 P 是 E 的聚点. 聚点可以属于 E , 也可以不属于 E (因为聚点可以为 所有聚点所成的点集成为 E 的导集 . E 的边界点 ) (2) 聚点

(3)开区域及闭区域 ●若点集E的点都是内点,则称E为开集; ·E的边界,点的全体称为E的边界,记作OE; ·若,点集EOE,则称E为闭集; ·若集D中任意两点都可用一完全属于D的折线相连, 则称D是连通的; ·连通的开集称为开区域,简称区域; ·开区域连同它的边界一起称为闭区域 2009年7月5日星期日 9 目录 上页>下页 、返回
2009年7月5日星期日 9 目录 上页 下页 返回 D • 若点集 E 的点都是内点,则称 E 为开集; • 若点集 E ⊃∂E , 则称 E 为闭集; • 若集 D 中任意两点都可用一完全属于 D 的折线相连 , • 开区域连同它的边界一起称为闭区域. 则称 D 是连通的 ; • 连通的开集称为开区域 ,简称区域 ; . . • E 的边界点的全体称为 E 的边界, 记作 ∂E ; (3) 开区域及闭区域
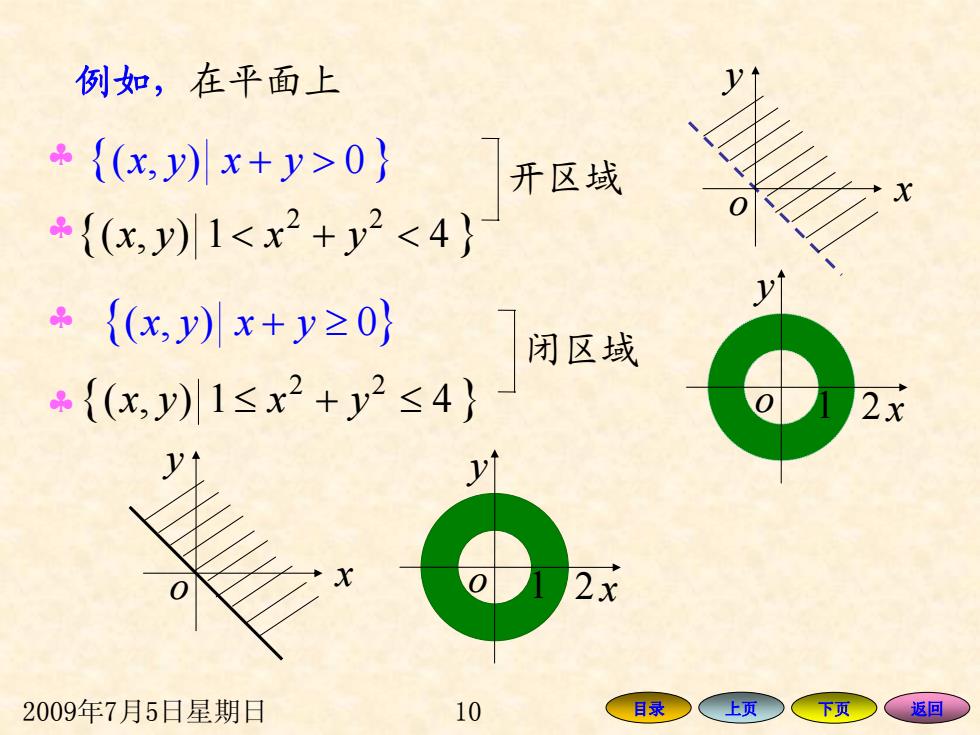
例如,在平面上 {(xy)x+y>0} 开区域 {(x,y)1<x2+y2<4} ÷{(xy)x+y≥0} 闭区域 {(x,y)1≤x2+y2≤4} 2x 2x 2009年7月5日星期日 10 目录○ 、上页 (下页 返回
2009年7月5日星期日 10 目录 上页 下页 返回 { yxyx >+ 0),( } { 1),( 4 } 22 yxyx <+< { + yxyx ≥ 0),( } { 1),( 4 } 22 yxyx ≤+≤ 开区域 闭区域 ♣ ♣ ♣ ♣ x y o 1 2 x y o x y o x y o 1 2 例如,在平面上

品整个平面是最大的开域, 也是最大的闭域; 点集{(x,y)x>}是开集, 但非区域 ·对区域D,若存在正数K,使一切点PD与某定点 A的距离AP飞K,则称D为有界域,否则称为无 界域 2009年7月5日星期日 11 目录○ (上页今下页 、返回
2009年7月5日星期日 11 目录 上页 下页 返回 ♣ 整个平面 ♣ 点集 { xyx >1),( }是开集, 是最大的开域 , 也是最大的闭域; 但非区域 . − 1 o 1 x y • 对区域 D , 若存在正数 K , 使一切点 P ∈D 与某定点 A 的距离 ⎜AP⎥≤ K , 则称 D 为有界域 , 否则称为 无 界域