
第三章 第四节函数的单调性 与曲孩的凹凸性 Monotonicity of Function Concavity and Convexity of Curve) 一、函数单调性的判定法 二、函数的凹凸性及拐点 三、小结与思考练习 2009年7月3日星期五 1 目录 上页 、返回
2009年7月3日星期五 1 目录 上页 下页 返回 第四节 函数的单调性 与曲线的凹凸性 第三章 三、小结与思考练习 二、 函数的凹凸性及拐点 一、函数单调性的判定法 (Monotonicity of Function & Concavity and Convexity of Curve)
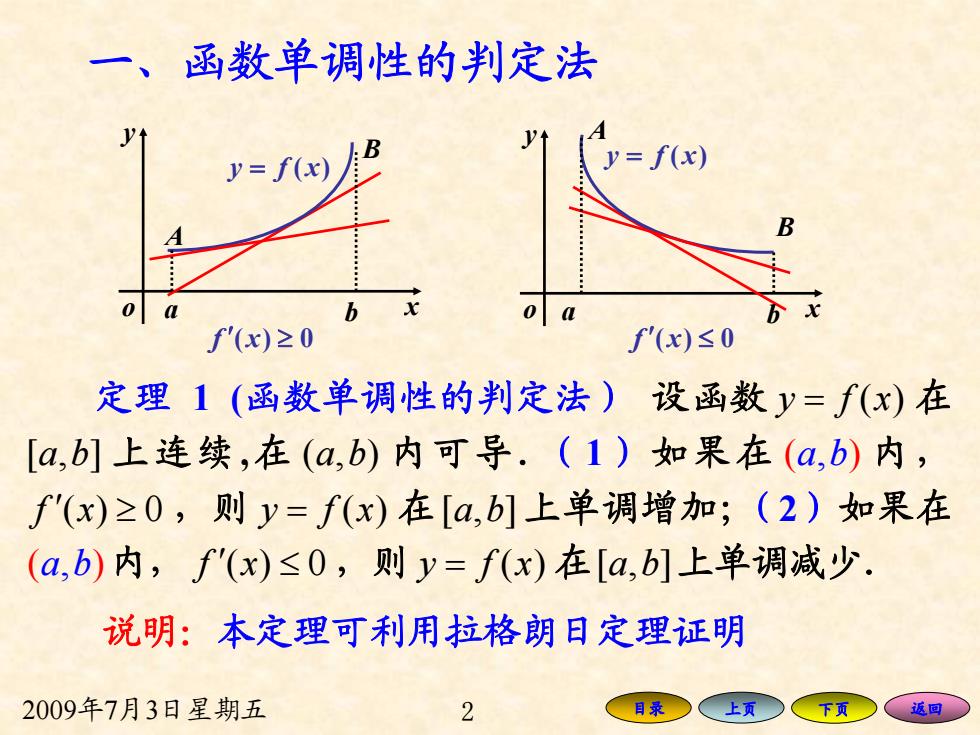
一、函数单调性的判定法 y=f(x) y=f(x) B 0 f'(x)≥0 f'(x)≤0 定理1(函数单调性的判定法)设函数y=f(x)在 [a,b]上连续,在(a,b)内可导.(1)如果在(a,b)内, f'(x)≥0,则y=f(x)在[a,b]上单调增加;(2)如果在 (a,b)内,f'(x)≤0,则y=f(x)在[a,b]上单调减少. 说明:本定理可利用拉格朗日定理证明 2009年7月3日星期五 2 目录 上页 返回
2009年7月3日星期五 2 目录 上页 下页 返回 一、函数单调性的判定法 定理 1 (函数单调性的判定法) 设函数 y fx = ( ) 在 [,] a b 上连续,在 (,) a b 内可导.(1)如果在 ( ) a b, 内, f x ′() 0 ≥ ,则 y fx = ( ) 在[,] a b 上单调增加;(2)如果在 ( ) a b, 内, f x ′() 0 ≤ ,则 y fx = ( ) 在[,] a b 上单调减少. x y o = fy x)( x y o = fy x)( a b A B f ′ x ≥ 0)( f ′ x ≤ 0)( a b B A 说明:本定理可利用拉格朗日定理证明

1.利用导数来判定函数的单调性 例1讨论函数f(x)=x3-3x2-9x+5的单调性. (课本例2) 解:这个函数的定义域为(-0,+0). 而f'(x)=3x2-6x-9=3(x+1)(x-3) 在(-0,-1)和(3,+∞)内,f'(x)>0,所以函数f(x) 在(-0,-1]和[3,+0)内单调增加. 在(-1,3)内,f'(x)<0,所以函数f(x)在[-1,3]内 单调减少 2009年7月3日星期五 3 目录 上页( 、返回
2009年7月3日星期五 3 目录 上页 下页 返回 例 1 讨论函数 3 2 fx x x x () 3 9 5 = − −+ 的单调性. (课本 例 2) 解: 这个函数的定义域为(,) 1. 利用导数来判定函数的单调性 −∞ +∞ . 而 2 fx x x x x ′( ) 3 6 9 3( 1)( 3) = − −= + − 在( , 1) −∞ − 和(3, ) +∞ 内, f x ′() 0 > ,所以函数 f x( ) 在( , 1] −∞ − 和[3, ) +∞ 内单调增加. 在( 1,3) − 内, f x ′() 0 < ,所以函数 f ( ) x 在[ 1,3] − 内 单调减少.

例2讨论函数y=x2的单调性.(课本例3) 解:D:(-o,十∞). f'(x)= 2 3x’ (x≠0) y=Vx2 当x=0时,导数不存在. 当-o00,.[0,+o]上单调增加; 单调区间为(-0,0,[0,+o). 注意:学习课本例3与例4之间的一段话 2009年7月3日星期五 目录 上页 返回
2009年7月3日星期五 4 目录 上页 下页 返回 解:∵ D +∞−∞ ).,(: )0(, 3 2 )( 3 ′ = x ≠ x xf 3 2 = xy 例 2 讨论函数 3 2 y = x 的单调性.(课本 例 3) 当 x = 0 时,导数不存在. 当−∞ ,∴[0, ] +∞ 上单调增加; 单调区间为 −∞ ]0,( , +∞).,0[ 注意:学习课本例 3 与例 4 之间的一段话

例3确定函数f(x)=(2x-5)x2的单调区间. (课本例4) 基本步骤: (1)确定定义区间; (2)求函数f(x)的导数; (3)找出驻点(导数为零的点)和导数不存在点; (4)以驻点和导数不存在点为分界点,把定义区间分 成若干个小区间,并讨论在这些小区间上,导数的符 号,进而确定单调区间。 2009年7月3日星期五 5 目录 上页 、返回
2009年7月3日星期五 5 目录 上页 下页 返回 例 3 确定函数 3 2 f ( ) (2 5) xx x = − 的单调区间. (课本 例 4) 基本步骤: (1)确定定义区间; (2)求函数f ( x )的导数; (3)找出驻点(导数为零的点)和导数不存在点; (4)以驻点和导数不存在点为分界点,把定义区间分 成若干个小区间,并讨论在这些小区间上,导数的符 号,进而确定单调区间

2.利用导数来证明不等式 例4当x>0时.试证x>ln(1+x)成立。 (补充题) 证明:令f(x)=x-ln(1+x),则f'(x)= 1+x 因为f(x)在[0,+0)上连续,且在(0,+0)内可导 f'(x)>0,所以f(x)在[0,+o)单调增加。 从而,当x>0时.有f(x)>f(0)成立。 即x-ln(1+x)>0成立,也即x>ln(1+x)成立。 2009年7月3日星期五 6 目录 上页 返回
2009年7月3日星期五 6 目录 上页 下页 返回 2. 利用导数来证明不等式 例 4 当 x > 0 时.试证 x x > + ln(1 ) 成立。 (补充题) 证明: 令 f ( ) ln(1 ), xx x = − + 则 () . 1 x f x x ′ = + 因为 f ( ) x 在[0, ) +∞ 上连续,且在(0, ) +∞ 内可导 f x ′( ) 0, > 所以 f ( ) x 在[0, ) +∞ 单调增加。 从而,当 x > 0 时.有 f ( ) (0) x > f 成立。 即 x x − +> ln(1 ) 0 成立,也即 x > + ln(1 ) x 成立

3.利用导数来证明方程根的唯一性 例5设a2-3b<0,证明:实系数方程 x3+ax2+bx+c=0 的实根是唯一的. (课本例6) 提示:令f(x)=x3+ax2+bx+c (1)利用零,点定理证存在性。 (2)利用导数证明函数单调,从而证明根的唯一性 2009年7月3日星期五 7 目录 上页( 下 、返回
2009年7月3日星期五 7 目录 上页 下页 返回 3. 利用导数来证明方程根的唯一性 例 5 设 2 a b − 3 0 < ,证明:实系数方程 3 2 x ax bx c + + += 0 的实根是唯一的. (课本 例 6) 提示: 令 3 2 f ( ) x x ax bx c = + ++ (1)利用零点定理证存在性。 (2)利用导数证明函数单调,从而证明根的唯一性

二、函数的凹凸性及拐,点(Inflection Point) 1、曲线凹凸的定义 B 显然,曲线AB与BC都是单调增加的,但它们单调 增加的变化方式却有所不同。这说明:仅靠单调性来 描述曲线的性态是不够的。 为此,我们有必要研究一下曲线的弯曲方向问题。 2009年7月3日星期五 8 目录 上页
2009年7月3日星期五 8 目录 上页 下页 返回 二、函数的凹凸性及拐点(Inflection Point) 1、曲线凹凸的定义 显然,曲线AB与BC 都是单调增加的, x y o A B C 但它们单调 增加的变化方式却有所不同。 这说明:仅靠单调性来 描述曲线的性态是不够的。 为此,我们有必要研究一下曲线的弯曲方向问题
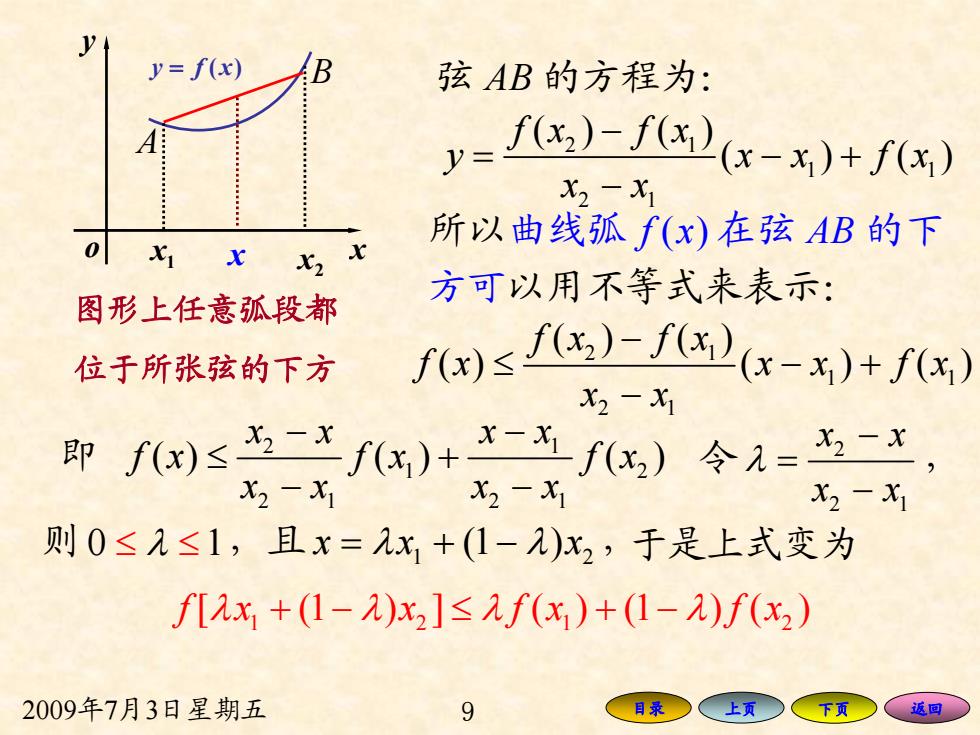
y=f(x) B 弦AB的方程为: y=,)-f(x-)+f) X2-x1 0 所以曲线孤f(x)在弦AB的下 方可以用不等式来表示: 图形上任意孤段都 位于所张弦的下方 f)sf,)-f(-x)+1x) X2-X1 即fx)≤5-fx)+-fx)令=-x X2-X1 X2-X1 X2-X1 则0≤2≤1,且x=九x1+(1-)x2,于是上式变为 f[2x,+(1-)x2]≤f(x)+(1-2)f(x2) 2009年7月3日星期五 9 目录 上页 返回
2009年7月3日星期五 9 目录 上页 下页 返回 x y o y = f x)( x1 2 x 图形上任意弧段都 位于所张弦的下方 A B 弦 AB 的方程为: 2 1 1 1 2 1 () () ( ) () fx fx y x x f x x x − = − + − 所以曲线弧 f ( ) x 在弦 AB 的下 方可以用不等式来表示: 2 1 1 1 2 1 () () ( ) ( ) ( ) fx fx f x x x f x x x − ≤ − + − 2 1 1 2 21 21 () ( ) ( ) x x xx f x f x f x xx xx − − ≤ + − − 即 令 2 2 1 x x x x λ − = − , 则0 1 ≤ λ ≤ ,且 1 2 xx x = +− λ (1 ) λ ,于是上式变为 1 21 2 f [ (1 ) ] ( ) (1 ) ( ) λ λλ λ x x +− ≤ +− f x f x x

定义设函数f(x)在区间I上连续,如果对I上任意 两,点x,x2(不妨设x<x2)及任意正数(0≤≤1),恒 有 f[2x+(1-2)x2]≤2f(x)+(1-2)f(x2), 则称曲线y=f(x)在I上是凹的. 类似地,可给出曲线是凸的定义,若上式中不等 号反向,则称曲线y=f(x)在I上是凸的. 直接利用定义来判别曲线的凹凸性是比较困难的, 下面利用二阶导数来判别曲线的凹凸性. 2009年7月3日星期五 10 日录 上页 返回
2009年7月3日星期五 10 目录 上页 下页 返回 定义 设函数 f x( ) 在区间 I 上连续,如果对 I 上任意 两点 1 2 x x, (不妨设 1 2 x x < )及任意正数λ(0 1) ≤ λ ≤ ,恒 有 1 21 2 f [ (1 )) ] ( ) (1 ) ( ), λ λλ λ x x fx fx +− ≤ +− 则称曲线 y fx = ( ) 在 I 上是凹的. 类似地,可给出曲线是凸的定义,若上式中不等 号反向,则称曲线 y fx = ( ) 在 I 上是凸的. 直接利用定义来判别曲线的凹凸性是比较困难的, 下面利用二阶导数来判别曲线的凹凸性.