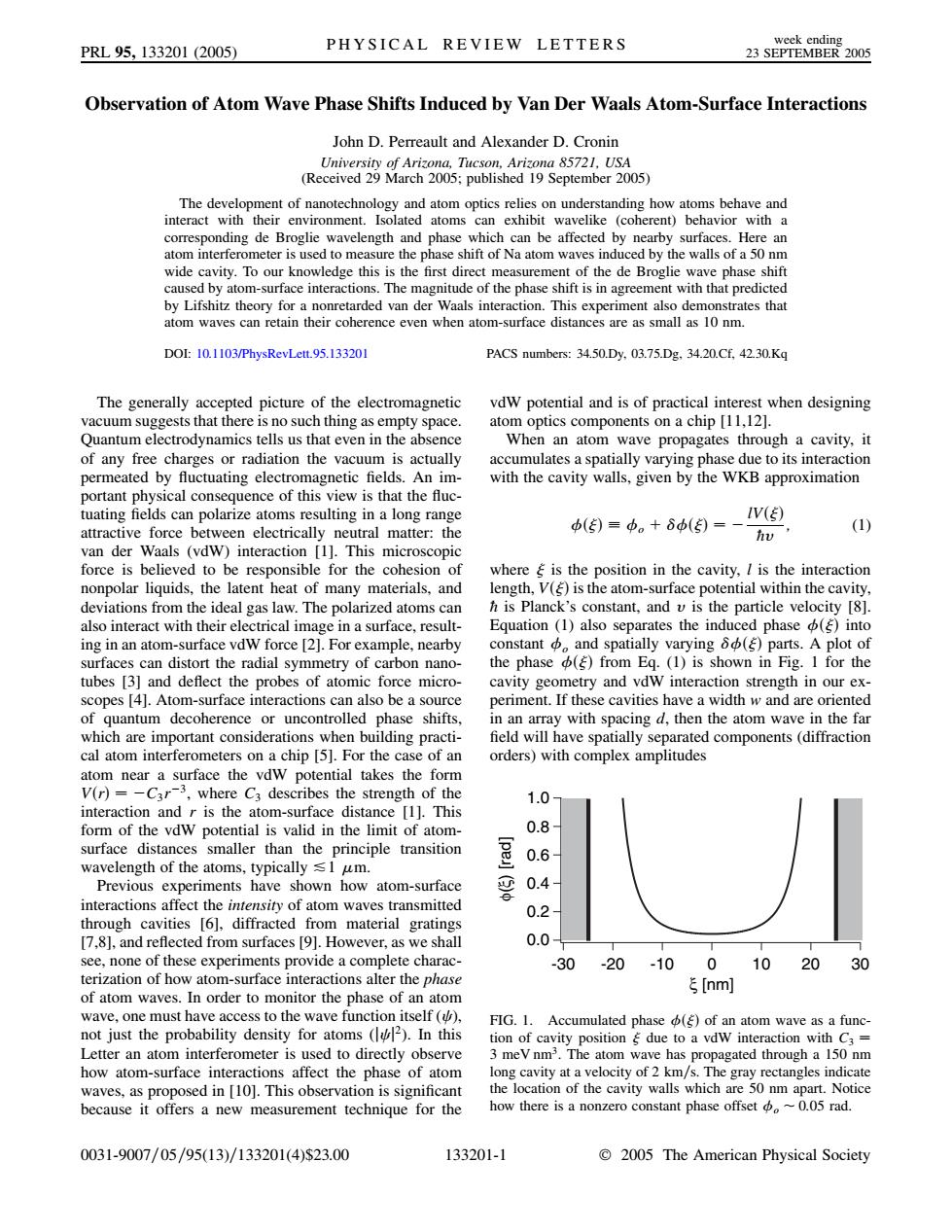
PRL95,133201(2005) PHYSICAL REVIEW LETTERS week ending 23 SEPTEMBER 2005 Observation of Atom Wave Phase Shifts Induced by Van Der Waals Atom-Surface Interactions John D.Perreault and Alexander D.Cronin University of Arizona,Tucson,Arizona 85721.USA (Received 29 March 2005;published 19 September 2005) The development of nanotechnology and atom optics relies on understanding how atoms behave and interact with their environment.Isolated atoms can exhibit wavelike (coherent)behavior with a corresponding de Broglie wavelength and phase which can be affected by nearby surfaces.Here an atom interferometer is used to measure the phase shift of Na atom waves induced by the walls of a 50 nm wide cavity.To our knowledge this is the first direct measurement of the de Broglie wave phase shift caused by atom-surface interactions.The magnitude of the phase shift is in agreement with that predicted by Lifshitz theory for a nonretarded van der Waals interaction.This experiment also demonstrates that atom waves can retain their coherence even when atom-surface distances are as small as 10 nm. DOI:10.1103/PhysRevLett.95.133201 PACS numbers:34.50.Dy.03.75.Dg,34.20.Cf,42.30.Kg The generally accepted picture of the electromagnetic vdW potential and is of practical interest when designing vacuum suggests that there is no such thing as empty space. atom optics components on a chip [11,12]. Quantum electrodynamics tells us that even in the absence When an atom wave propagates through a cavity,it of any free charges or radiation the vacuum is actually accumulates a spatially varying phase due to its interaction permeated by fluctuating electromagnetic fields.An im- with the cavity walls,given by the WKB approximation portant physical consequence of this view is that the fluc- tuating fields can polarize atoms resulting in a long range attractive force between electrically neutral matter:the ()=。+6b()=-V(包 (1) van der Waals (vdw)interaction [1].This microscopic force is believed to be responsible for the cohesion of where is the position in the cavity,I is the interaction nonpolar liquids,the latent heat of many materials,and length,V()is the atom-surface potential within the cavity, deviations from the ideal gas law.The polarized atoms can h is Planck's constant,and v is the particle velocity [8]. also interact with their electrical image in a surface,result- Equation (1)also separates the induced phase (into ing in an atom-surface vdW force [2].For example,nearby constant中。and spatially varying 6中()parts.A plot of surfaces can distort the radial symmetry of carbon nano- the phase (from Eq.(1)is shown in Fig.I for the tubes [3]and deflect the probes of atomic force micro- cavity geometry and vdW interaction strength in our ex- scopes [4].Atom-surface interactions can also be a source periment.If these cavities have a width w and are oriented of quantum decoherence or uncontrolled phase shifts, in an array with spacing d,then the atom wave in the far which are important considerations when building practi- field will have spatially separated components(diffraction cal atom interferometers on a chip [5].For the case of an orders)with complex amplitudes atom near a surface the vdw potential takes the form V(r)=-C3r-3,where C3 describes the strength of the 1.0 interaction and r is the atom-surface distance [1].This form of the vdw potential is valid in the limit of atom- 0.8 surface distances smaller than the principle transition pe 0.6 wavelength of the atoms,typically 1 um. Previous experiments have shown how atom-surface 0.4 e interactions affect the intensity of atom waves transmitted 0.2 through cavities [6],diffracted from material gratings [7,8],and reflected from surfaces [9].However,as we shall 0.0 see,none of these experiments provide a complete charac- -30 -20-100 1020 30 terization of how atom-surface interactions alter the phase ξ[nm of atom waves.In order to monitor the phase of an atom wave,one must have access to the wave function itself(), FIG.1.Accumulated phase (of an atom wave as a func- not just the probability density for atoms(2).In this tion of cavity position due to a vdw interaction with C3= Letter an atom interferometer is used to directly observe 3 meV nm3.The atom wave has propagated through a 150 nm how atom-surface interactions affect the phase of atom long cavity at a velocity of 2 km/s.The gray rectangles indicate waves,as proposed in [10].This observation is significant the location of the cavity walls which are 50 nm apart.Notice because it offers a new measurement technique for the how there is a nonzero constant phase offset ~0.05 rad. 0031-9007/05/95(13)/133201(4)$23.00 133201-1 2005 The American Physical SocietyObservation of Atom Wave Phase Shifts Induced by Van Der Waals Atom-Surface Interactions John D. Perreault and Alexander D. Cronin University of Arizona, Tucson, Arizona 85721, USA (Received 29 March 2005; published 19 September 2005) The development of nanotechnology and atom optics relies on understanding how atoms behave and interact with their environment. Isolated atoms can exhibit wavelike (coherent) behavior with a corresponding de Broglie wavelength and phase which can be affected by nearby surfaces. Here an atom interferometer is used to measure the phase shift of Na atom waves induced by the walls of a 50 nm wide cavity. To our knowledge this is the first direct measurement of the de Broglie wave phase shift caused by atom-surface interactions. The magnitude of the phase shift is in agreement with that predicted by Lifshitz theory for a nonretarded van der Waals interaction. This experiment also demonstrates that atom waves can retain their coherence even when atom-surface distances are as small as 10 nm. DOI: 10.1103/PhysRevLett.95.133201 PACS numbers: 34.50.Dy, 03.75.Dg, 34.20.Cf, 42.30.Kq The generally accepted picture of the electromagnetic vacuum suggests that there is no such thing as empty space. Quantum electrodynamics tells us that even in the absence of any free charges or radiation the vacuum is actually permeated by fluctuating electromagnetic fields. An im￾portant physical consequence of this view is that the fluc￾tuating fields can polarize atoms resulting in a long range attractive force between electrically neutral matter: the van der Waals (vdW) interaction [1]. This microscopic force is believed to be responsible for the cohesion of nonpolar liquids, the latent heat of many materials, and deviations from the ideal gas law. The polarized atoms can also interact with their electrical image in a surface, result￾ing in an atom-surface vdW force [2]. For example, nearby surfaces can distort the radial symmetry of carbon nano￾tubes [3] and deflect the probes of atomic force micro￾scopes [4]. Atom-surface interactions can also be a source of quantum decoherence or uncontrolled phase shifts, which are important considerations when building practi￾cal atom interferometers on a chip [5]. For the case of an atom near a surface the vdW potential takes the form V
rC3r3, where C3 describes the strength of the interaction and r is the atom-surface distance [1]. This form of the vdW potential is valid in the limit of atom￾surface distances smaller than the principle transition wavelength of the atoms, typically &1
m. Previous experiments have shown how atom-surface interactions affect the intensity of atom waves transmitted through cavities [6], diffracted from material gratings [7,8], and reflected from surfaces [9]. However, as we shall see, none of these experiments provide a complete charac￾terization of how atom-surface interactions alter the phase of atom waves. In order to monitor the phase of an atom wave, one must have access to the wave function itself ( ), not just the probability density for atoms (j j 2). In this Letter an atom interferometer is used to directly observe how atom-surface interactions affect the phase of atom waves, as proposed in [10]. This observation is significant because it offers a new measurement technique for the vdW potential and is of practical interest when designing atom optics components on a chip [11,12]. When an atom wave propagates through a cavity, it accumulates a spatially varying phase due to its interaction with the cavity walls, given by the WKB approximation
 o  
 lV
@v ; (1) where is the position in the cavity, l is the interaction length, V
is the atom-surface potential within the cavity, @ is Planck’s constant, and v is the particle velocity [8]. Equation (1) also separates the induced phase
into constant o and spatially varying 
parts. A plot of the phase
from Eq. (1) is shown in Fig. 1 for the cavity geometry and vdW interaction strength in our ex￾periment. If these cavities have a width w and are oriented in an array with spacing d, then the atom wave in the far field will have spatially separated components (diffraction orders) with complex amplitudes 1.0 0.8 0.6 0.4 0.2 0.0 φ(ξ) [rad] -30 -20 -10 0 10 20 30 ξ [nm] FIG. 1. Accumulated phase
of an atom wave as a func￾tion of cavity position due to a vdW interaction with C3 3 meV nm3. The atom wave has propagated through a 150 nm long cavity at a velocity of 2 km=s. The gray rectangles indicate the location of the cavity walls which are 50 nm apart. Notice how there is a nonzero constant phase offset o  0:05 rad. PRL 95, 133201 (2005) PHYSICAL REVIEW LETTERS week ending 23 SEPTEMBER 2005 0031-9007=05=95(13)=133201(4)$23.00 133201-1 © 2005 The American Physical Society