正在加载图片...
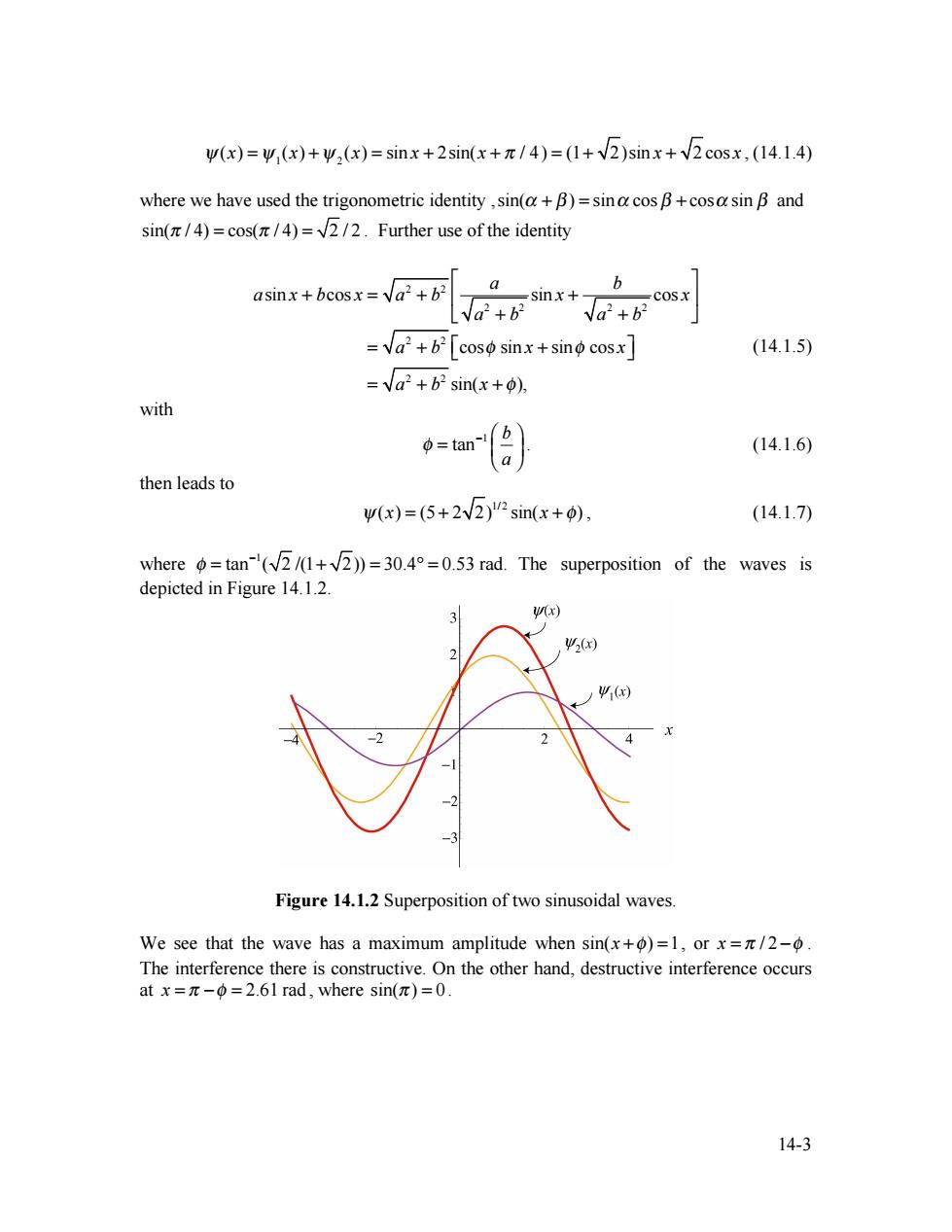
W(x)=W(x)+w,(x)=sinx+2sin(x+/4)=(1+2)sinx+2cosx,(14.1.4) where we have used the trigonometric identity,sin(a+B)=sina cos B+cosa sin B and sin(/4)=cos(/4)=2/2.Further use of the identity asinx+bcosx=a2+b2 _sinx+ √a+ =a2+b2[coso sinx+sino cosx (14.1.5) =√a2+b2sin(x+p), with =tan a (14.1.6) then leads to w(x)=(5+2v2)"sin(x+0), (14.1.7) where =tan-(+))=30.4=0.53 rad.The superposition of the waves is depicted in Figure 14.1.2. 3 W(x) 2(x) ) -2 Figure 14.1.2 Superposition of two sinusoidal waves. We see that the wave has a maximum amplitude when sin(x+)=1,or x=/2-6. The interference there is constructive.On the other hand,destructive interference occurs atx=π-Φ=2.6lrad,where sin(π)=0. 14-314-3 ψ(x) = ψ1(x) +ψ 2 (x) = sin x + 2sin(x + π / 4) = (1+ 2)sin x + 2 cos x , (14.1.4) where we have used the trigonometric identity ,sin(α + β ) = sinα cos β + cosα sin β and sin(π / 4) = cos(π / 4) = 2 / 2 . Further use of the identity asin x + bcos x = a 2 + b2 a a 2 + b2 sin x + b a 2 + b2 cos x ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ = a 2 + b2 ⎡cosφ sin x + sinφ cos x ⎣ ⎤ ⎦ = a 2 + b2 sin(x + φ), (14.1.5) with 1 tan b a φ − ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ . (14.1.6) then leads to ψ(x) = (5 + 2 2) 1/ 2 sin(x + φ) , (14.1.7) where 1 φ tan ( 2 /(1 2)) 30.4 0.53 rad. − = + = ° = The superposition of the waves is depicted in Figure 14.1.2. Figure 14.1.2 Superposition of two sinusoidal waves. We see that the wave has a maximum amplitude when sin(x +φ) =1, or x = π / 2 −φ . The interference there is constructive. On the other hand, destructive interference occurs at x = π −φ = 2.61 rad , where sin(π ) = 0