
Chapter 14 Interference and Diffraction 14.1 Superposition of Waves....................... 14-2 14.1.1 Interference Conditions for Light Sources.... 14-4 14.2 Young's Double-Slit Experiment..... 14-4 Example 14.1:Double-Slit Experiment................ 14-8 14.3 Intensity Distribution 14-8 Example 14.2:Intensity of Three-Slit Interference... 14-11 14.4 Diffraction............. 14-13 14.5 Single-Slit Diffraction.................. 14-14 Example 14.3:Single-Slit Diffraction............ 14-16 14.6 Intensity of Single-Slit Diffraction..... 14-17 14.7 Intensity of Double-Slit Diffraction Patterns. 14-21 14.8 Diffraction Grating.. 14-22 14.9 Summary.… 14-23 14.10 Appendix:Computing the Total Electric Field... 14-24 14.11 Solved Problems ............... 14-28 14.11.1 Double-Slit Experiment.................... 14-28 14.11.2 Phase Difference................ 14-29 14.11.3 Constructive Interference................ 14-30 14.11.4 Intensity in Double-Slit Interference 14-31 14.11.5 Second-Order Bright Fringe........ 14-32 14.11.6 Intensity in Double-Slit Diffraction.. 14-32 14.12 Conceptual Questions................. 14-35 14.13 Additional Problems..... 14-35 14.13.1 Double-Slit Interference..... .14-35 14.13.2 Interference-Diffraction Pattern.. 14-36 14.13.3 Three-Slit Interference..... 14-36 14.13.4 Intensity of Double-Slit Interference........................... 14-36 14.13.5 Secondary Maxima............ 14-36 14.13.6 Interference-Diffraction Pattern. 14-37 14-1
14-1 Chapter 14 Interference and Diffraction 14.1 Superposition of Waves................................................................................... 14-2 14.1.1 Interference Conditions for Light Sources............................................... 14-4 14.2 Young’s Double-Slit Experiment .................................................................... 14-4 Example 14.1: Double-Slit Experiment................................................................. 14-8 14.3 Intensity Distribution ....................................................................................... 14-8 Example 14.2: Intensity of Three-Slit Interference ............................................. 14-11 14.4 Diffraction...................................................................................................... 14-13 14.5 Single-Slit Diffraction.................................................................................... 14-14 Example 14.3: Single-Slit Diffraction ................................................................. 14-16 14.6 Intensity of Single-Slit Diffraction ................................................................ 14-17 14.7 Intensity of Double-Slit Diffraction Patterns................................................. 14-21 14.8 Diffraction Grating......................................................................................... 14-22 14.9 Summary........................................................................................................ 14-23 14.10 Appendix: Computing the Total Electric Field.............................................. 14-24 14.11 Solved Problems ............................................................................................ 14-28 14.11.1 Double-Slit Experiment ....................................................................... 14-28 14.11.2 Phase Difference .................................................................................. 14-29 14.11.3 Constructive Interference..................................................................... 14-30 14.11.4 Intensity in Double-Slit Interference ................................................... 14-31 14.11.5 Second-Order Bright Fringe ................................................................ 14-32 14.11.6 Intensity in Double-Slit Diffraction..................................................... 14-32 14.12 Conceptual Questions .................................................................................... 14-35 14.13 Additional Problems ...................................................................................... 14-35 14.13.1 Double-Slit Interference....................................................................... 14-35 14.13.2 Interference-Diffraction Pattern........................................................... 14-36 14.13.3 Three-Slit Interference ......................................................................... 14-36 14.13.4 Intensity of Double-Slit Interference ................................................... 14-36 14.13.5 Secondary Maxima .............................................................................. 14-36 14.13.6 Interference-Diffraction Pattern........................................................... 14-37

Interference and Diffraction 14.1 Superposition of Waves Consider a region in space where two or more waves pass through at the same time. According to the superposition principle,the net displacement is simply given by the vector or the algebraic sum of the individual displacements.Interference is the combination of two or more waves to form a composite wave,based on such principle. The idea of the superposition principle is illustrated in Figure 14.1.1. constructive interference b) Figure 14.1.1 Superposition of waves.(a)Traveling wave pulses approach each other, (b)constructive interference,(c)destructive interference,(d)waves move apart. Suppose we are given two waves, y(x,t)=Ψ。sin(kx±0t+9) Ψ2(x,1)=Ψ20sin(kx±0,1+,).(14.1.1) The resulting sum of the two waves is y(x,)=Ψosin(kx±ω,t+9)+Ψ2osin(k3x±ω,1+92) (14.1.2) The interference is constructive if the amplitude of y(x,t)is greater than the individual ones(Figure 14.1.1b),and destructive if smaller (Figure 14.1.1c). As an example,consider the superposition of the following two waves at t=0: y,(x)=sinx,Ψ,(x)=2sin(x+π/4) (14.1.3) The resultant wave is given by 14-2
14-2 Interference and Diffraction 14.1 Superposition of Waves Consider a region in space where two or more waves pass through at the same time. According to the superposition principle, the net displacement is simply given by the vector or the algebraic sum of the individual displacements. Interference is the combination of two or more waves to form a composite wave, based on such principle. The idea of the superposition principle is illustrated in Figure 14.1.1. (a) (b) (c) (d) Figure 14.1.1 Superposition of waves. (a) Traveling wave pulses approach each other, (b) constructive interference, (c) destructive interference, (d) waves move apart. Suppose we are given two waves, ψ 1 (x,t) = ψ 10 sin(k1 x ± ω1 t + φ1 ), ψ 2 (x,t) = ψ 20 sin(k2 x ±ω2 t + φ2 ). (14.1.1) The resulting sum of the two waves is ψ (x,t) = ψ10 sin(k1 x ±ω1 t + φ1) +ψ 20 sin(k2 x ±ω2 t + φ2 ). (14.1.2) The interference is constructive if the amplitude of ψ (x,t) is greater than the individual ones (Figure 14.1.1b), and destructive if smaller (Figure 14.1.1c). As an example, consider the superposition of the following two waves at t = 0 : ψ1(x) = sin x, ψ 2 (x) = 2sin(x + π / 4) (14.1.3) The resultant wave is given by
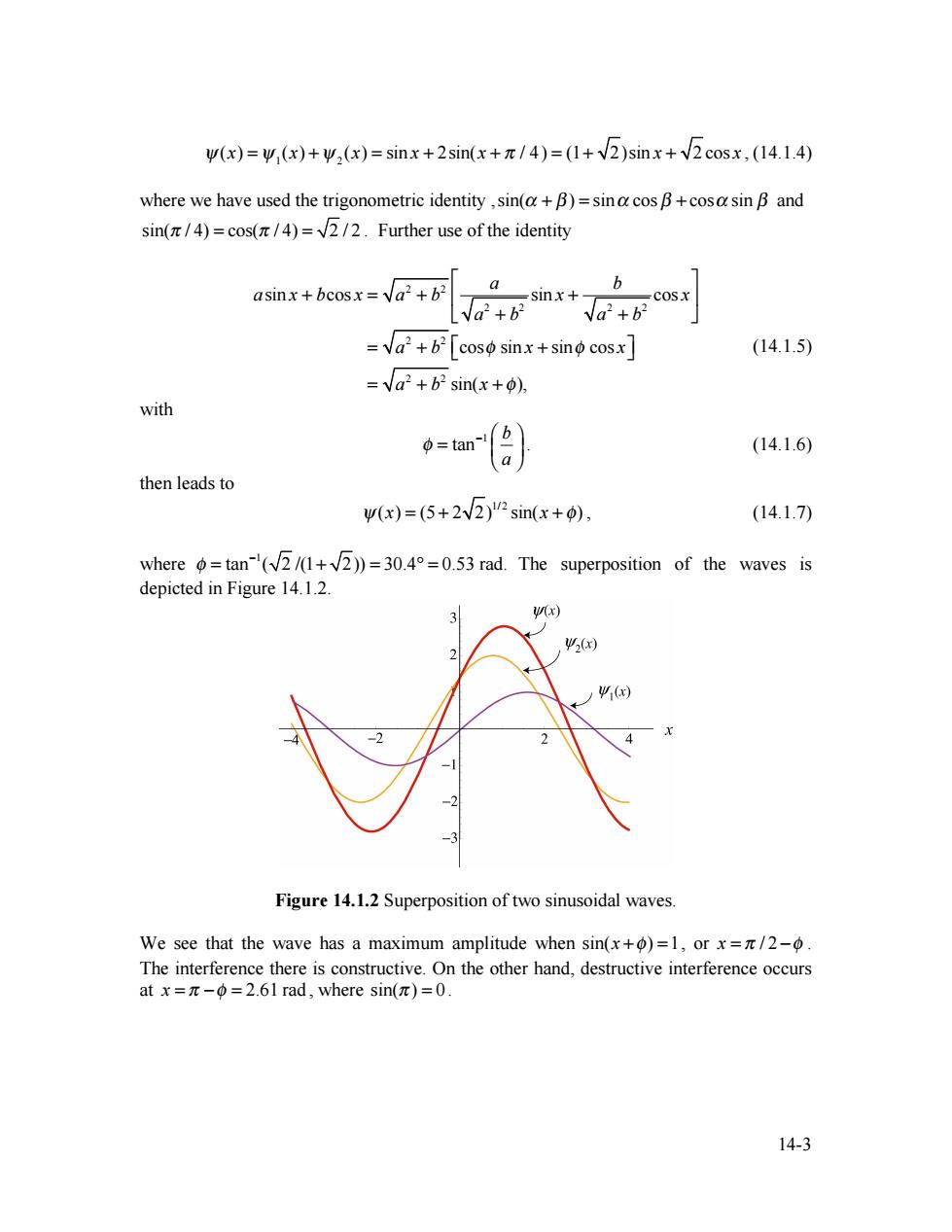
W(x)=W(x)+w,(x)=sinx+2sin(x+/4)=(1+2)sinx+2cosx,(14.1.4) where we have used the trigonometric identity,sin(a+B)=sina cos B+cosa sin B and sin(/4)=cos(/4)=2/2.Further use of the identity asinx+bcosx=a2+b2 _sinx+ √a+ =a2+b2[coso sinx+sino cosx (14.1.5) =√a2+b2sin(x+p), with =tan a (14.1.6) then leads to w(x)=(5+2v2)"sin(x+0), (14.1.7) where =tan-(+))=30.4=0.53 rad.The superposition of the waves is depicted in Figure 14.1.2. 3 W(x) 2(x) ) -2 Figure 14.1.2 Superposition of two sinusoidal waves. We see that the wave has a maximum amplitude when sin(x+)=1,or x=/2-6. The interference there is constructive.On the other hand,destructive interference occurs atx=π-Φ=2.6lrad,where sin(π)=0. 14-3
14-3 ψ(x) = ψ1(x) +ψ 2 (x) = sin x + 2sin(x + π / 4) = (1+ 2)sin x + 2 cos x , (14.1.4) where we have used the trigonometric identity ,sin(α + β ) = sinα cos β + cosα sin β and sin(π / 4) = cos(π / 4) = 2 / 2 . Further use of the identity asin x + bcos x = a 2 + b2 a a 2 + b2 sin x + b a 2 + b2 cos x ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ = a 2 + b2 ⎡cosφ sin x + sinφ cos x ⎣ ⎤ ⎦ = a 2 + b2 sin(x + φ), (14.1.5) with 1 tan b a φ − ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠ . (14.1.6) then leads to ψ(x) = (5 + 2 2) 1/ 2 sin(x + φ) , (14.1.7) where 1 φ tan ( 2 /(1 2)) 30.4 0.53 rad. − = + = ° = The superposition of the waves is depicted in Figure 14.1.2. Figure 14.1.2 Superposition of two sinusoidal waves. We see that the wave has a maximum amplitude when sin(x +φ) =1, or x = π / 2 −φ . The interference there is constructive. On the other hand, destructive interference occurs at x = π −φ = 2.61 rad , where sin(π ) = 0

14.1.1 Interference Conditions for Light Sources Suppose we are considering two light waves.In order to form an interference pattern,the incident light must satisfy two conditions: (i)The light sources must be coherent.This means that the waves from the sources must maintain a constant phase relation.For example,if two waves are phase shifted by o=, this phase shift must not change with time. (ii)The light must be monochromatic.This means that the light consists of just one wavelengthλ=2π/k. Light emitted from an incandescent light bulb is incoherent because the light consists of waves of different wavelengths and they do not maintain a constant phase relationship. Thus,no interference pattern is observed. Figure 14.1.3 Incoherent light source 14.2 Young's Double-Slit Experiment In 1801 Thomas Young carried out an experiment in which the wave nature of light was demonstrated.The schematic diagram of the double-slit experiment is shown in Figure 14.2.1. naximum minimum maximum maximum Figure 14.2.1 Young's double-slit experiment. 14-4
14-4 14.1.1 Interference Conditions for Light Sources Suppose we are considering two light waves. In order to form an interference pattern, the incident light must satisfy two conditions: (i) The light sources must be coherent. This means that the waves from the sources must maintain a constant phase relation. For example, if two waves are phase shifted by φ = π , this phase shift must not change with time. (ii) The light must be monochromatic. This means that the light consists of just one wavelength λ = 2π / k . Light emitted from an incandescent light bulb is incoherent because the light consists of waves of different wavelengths and they do not maintain a constant phase relationship. Thus, no interference pattern is observed. Figure 14.1.3 Incoherent light source 14.2 Young’s Double-Slit Experiment In 1801 Thomas Young carried out an experiment in which the wave nature of light was demonstrated. The schematic diagram of the double-slit experiment is shown in Figure 14.2.1. Figure 14.2.1 Young’s double-slit experiment
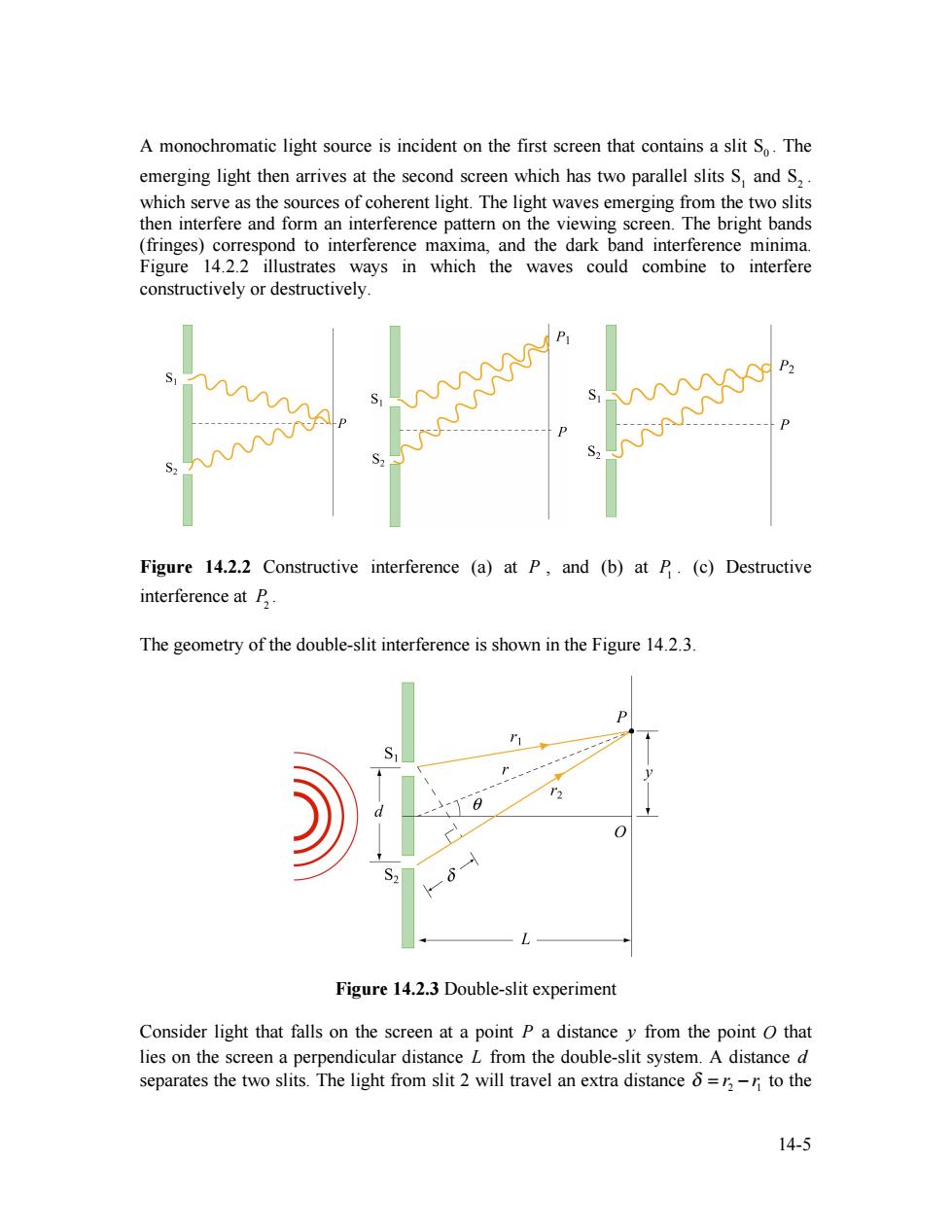
A monochromatic light source is incident on the first screen that contains a slit So.The emerging light then arrives at the second screen which has two parallel slits S,and S,. which serve as the sources of coherent light.The light waves emerging from the two slits then interfere and form an interference pattern on the viewing screen.The bright bands (fringes)correspond to interference maxima,and the dark band interference minima. Figure 14.2.2 illustrates ways in which the waves could combine to interfere constructively or destructively. P Figure 14.2.2 Constructive interference (a)at P,and (b)at P.(c)Destructive interference at B. The geometry of the double-slit interference is shown in the Figure 14.2.3. S Figure 14.2.3 Double-slit experiment Consider light that falls on the screen at a point P a distance y from the point O that lies on the screen a perpendicular distance L from the double-slit system.A distance d separates the two slits.The light from slit 2 will travel an extra distance =,-n to the 14-5
14-5 A monochromatic light source is incident on the first screen that contains a slit S0 . The emerging light then arrives at the second screen which has two parallel slits S1 and S2 . which serve as the sources of coherent light. The light waves emerging from the two slits then interfere and form an interference pattern on the viewing screen. The bright bands (fringes) correspond to interference maxima, and the dark band interference minima. Figure 14.2.2 illustrates ways in which the waves could combine to interfere constructively or destructively. Figure 14.2.2 Constructive interference (a) at P , and (b) at P1 . (c) Destructive interference at P2 . The geometry of the double-slit interference is shown in the Figure 14.2.3. Figure 14.2.3 Double-slit experiment Consider light that falls on the screen at a point P a distance y from the point O that lies on the screen a perpendicular distance L from the double-slit system. A distance d separates the two slits. The light from slit 2 will travel an extra distance 2 1 δ = r − r to the

point P than the light from slit 1.This extra distance is called the path difference.From Figure 14.2.3,we have,using the law of cosines, =r侣j-a任-+m. (14.2.1) and =r+-m任+r+侵 (14.2.2) Subtracting Eq.(142.1)from Eq.(14.2.2)yields 52-r2=(5+r)5-r)=2 drsin6. (14.2.3) In the limit L>>d,where the distance to the screen is much greater than the distance between the slits,the sum of n and r may be approximated by r+r=2r,and the path difference becomes δ=5-片=dsin6. (14.2.4) In this limit,the two rays ni and r are essentially treated as parallel (see Figure 14.2.4). S1 d '2 S2 8=r-r2=dsine Figure 14.2.4 Path difference between the two rays,assuming L>>d. Whether the two waves are in phase or out of phase is determined by the value of 8. Constructive interference occurs when is zero or an integer multiple of the wavelength 2, δn=dsin9n=m2,m=O,±l,±2,±3,.(constructive interference) (14.2.5) 14-6
14-6 point P than the light from slit 1. This extra distance is called the path difference. From Figure 14.2.3, we have, using the law of cosines, 2 2 2 2 2 1 cos sin 2 2 2 d d r r dr r dr π θ θ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ = + ⎜ ⎟ − ⎜ − ⎟ = + ⎜ ⎟ − ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ , (14.2.1) and 2 2 2 2 2 2 cos sin 2 2 2 d d r r dr r dr π θ θ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ = + ⎜ ⎟ − ⎜ + ⎟ = + ⎜ ⎟ + ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ . (14.2.2) Subtracting Eq. (142.1) from Eq. (14.2.2) yields 2 2 2 1 2 1 2 1 r − r = (r + r )(r − r ) = 2drsinθ . (14.2.3) In the limit L >> d , where the distance to the screen is much greater than the distance between the slits, the sum of 1 r and 2r may be approximated by 1 2 r + r ≈ 2r, and the path difference becomes 2 1 δ = r − r ≈ d sinθ . (14.2.4) In this limit, the two rays 1 r and 2r are essentially treated as parallel (see Figure 14.2.4). Figure 14.2.4 Path difference between the two rays, assuming L >> d . Whether the two waves are in phase or out of phase is determined by the value of δ . Constructive interference occurs when δ is zero or an integer multiple of the wavelength λ , δ m = d sinθ m = mλ, m = 0, ± 1, ± 2, ± 3, (constructive interference) , (14.2.5)
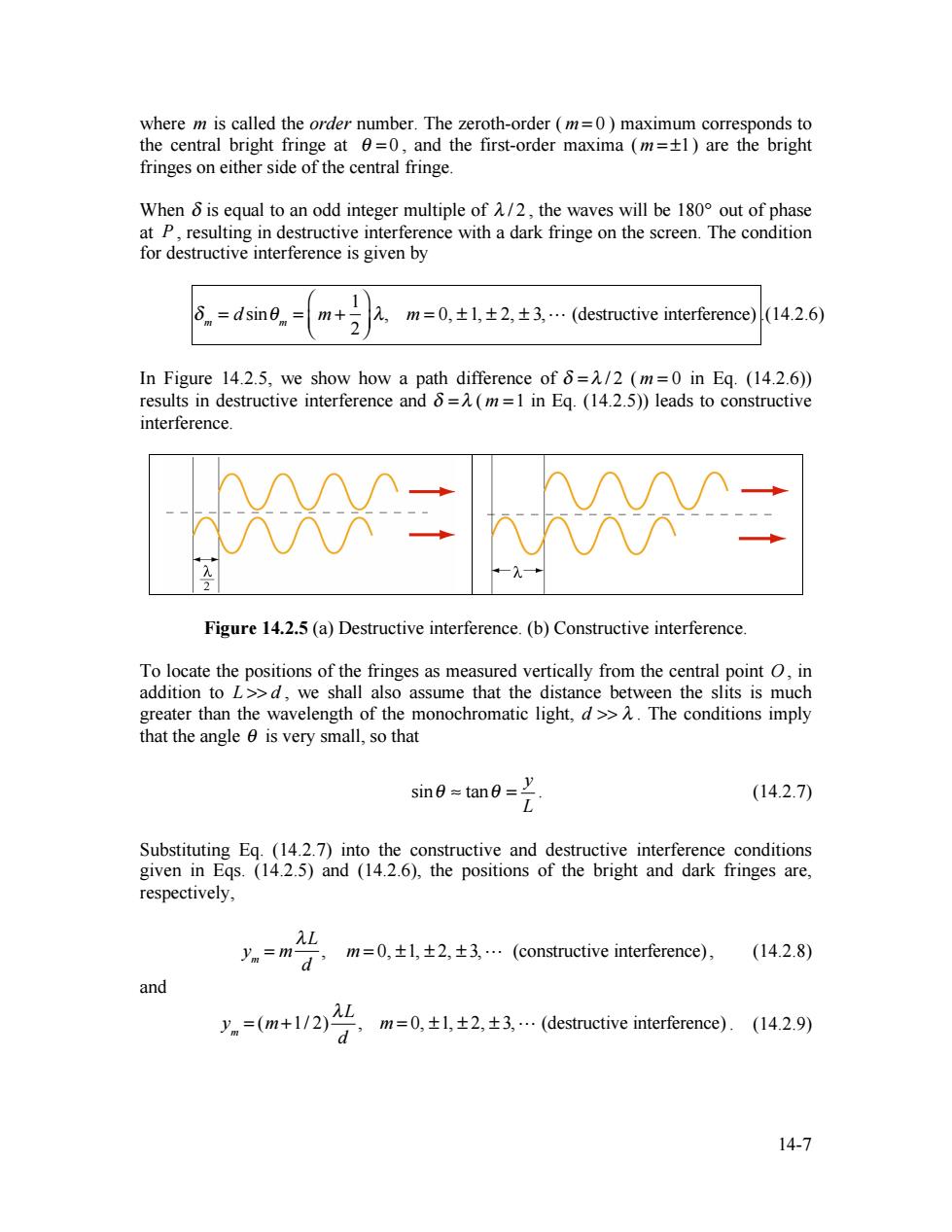
where m is called the order number.The zeroth-order (m=0)maximum corresponds to the central bright fringe at 0=0,and the first-order maxima (m=+1)are the bright fringes on either side of the central fringe. When 6 is equal to an odd integer multiple of A/2,the waves will be 180 out of phase at P,resulting in destructive interference with a dark fringe on the screen.The condition for destructive interference is given by δnm=dsin6n= m+2 2,m=0,±l,±2,±3,…(destructive interference) (14.2.6) In Figure 14.2.5,we show how a path difference of =/2 (m=0 in Eq.(14.2.6)) results in destructive interference and 6=(m=1 in Eq.(14.2.5))leads to constructive interference. XX二 Figure 14.2.5(a)Destructive interference.(b)Constructive interference To locate the positions of the fringes as measured vertically from the central point O,in addition to L>>d,we shall also assume that the distance between the slits is much greater than the wavelength of the monochromatic light,d>>.The conditions imply that the angle 0 is very small,so that sin=tan= (14.2.7) Substituting Eq.(14.2.7)into the constructive and destructive interference conditions given in Eqs.(14.2.5)and (14.2.6),the positions of the bright and dark fringes are, respectively, L y =m- a,m=0,±l,±2,±3…(oructiveinrrence)), (14.2.8) and =(m+1/2)2 ,m=0,±l,±2,±3,(destructiveintre).(l429y 14-7
14-7 where m is called the order number. The zeroth-order ( m = 0 ) maximum corresponds to the central bright fringe at θ = 0 , and the first-order maxima ( m = ±1) are the bright fringes on either side of the central fringe. When δ is equal to an odd integer multiple of λ / 2 , the waves will be 180° out of phase at P , resulting in destructive interference with a dark fringe on the screen. The condition for destructive interference is given by δ m = d sinθ m = m + 1 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ λ, m = 0, ± 1, ± 2, ± 3, (destructive interference) .(14.2.6) In Figure 14.2.5, we show how a path difference of δ = λ / 2 ( m = 0 in Eq. (14.2.6)) results in destructive interference and δ = λ ( m =1 in Eq. (14.2.5)) leads to constructive interference. Figure 14.2.5 (a) Destructive interference. (b) Constructive interference. To locate the positions of the fringes as measured vertically from the central point O , in addition to L >> d , we shall also assume that the distance between the slits is much greater than the wavelength of the monochromatic light, d >> λ . The conditions imply that the angle θ is very small, so that sin tan y L θ ≈ θ = . (14.2.7) Substituting Eq. (14.2.7) into the constructive and destructive interference conditions given in Eqs. (14.2.5) and (14.2.6), the positions of the bright and dark fringes are, respectively, ym = m λL d , m = 0, ±1, ± 2, ± 3, (constructive interference), (14.2.8) and ym = (m+1/ 2) λL d , m = 0, ±1, ± 2, ± 3, (destructive interference) . (14.2.9)
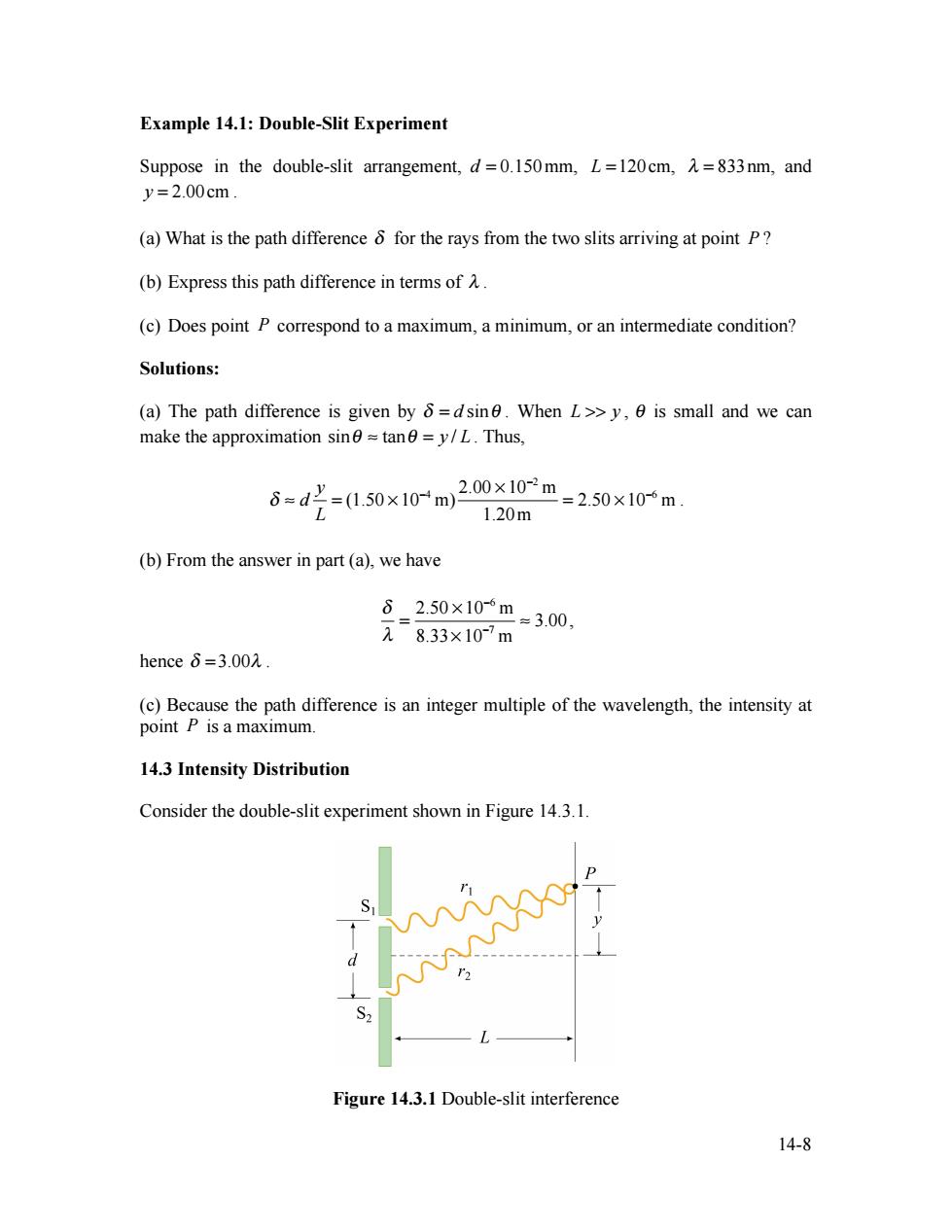
Example 14.1:Double-Slit Experiment Suppose in the double-slit arrangement,d=0.150mm,L=120cm,=833nm,and y=2.00cm. (a)What is the path difference 8 for the rays from the two slits arriving at point P? (b)Express this path difference in terms ofA. (c)Does point P correspond to a maximum,a minimum,or an intermediate condition? Solutions: (a)The path difference is given by 8=dsin.When L>>y,0 is small and we can make the approximation sin≈tanθ=y/L.Thus, 6=d'=(0.50×10-m 2.00×10-m=2.50×10m. 1.20m (b)From the answer in part(a),we have 62.50×10-6m 元8.33×10-7m =3.00, henceδ=3.002. (c)Because the path difference is an integer multiple of the wavelength,the intensity at point P is a maximum. 14.3 Intensity Distribution Consider the double-slit experiment shown in Figure 14.3.1. Figure 14.3.1 Double-slit interference 14-8
14-8 Example 14.1: Double-Slit Experiment Suppose in the double-slit arrangement, d = 0.150mm, L =120cm, λ = 833nm, and y = 2.00cm . (a) What is the path difference δ for the rays from the two slits arriving at point P ? (b) Express this path difference in terms of λ . (c) Does point P correspond to a maximum, a minimum, or an intermediate condition? Solutions: (a) The path difference is given by δ = d sinθ . When L >> y , θ is small and we can make the approximation sinθ ≈ tanθ = y / L . Thus, δ ≈ d y L = (1.50 × 10−4 m) 2.00 × 10−2 m 1.20m = 2.50 × 10−6 m . (b) From the answer in part (a), we have δ λ = 2.50 × 10−6 m 8.33× 10−7 m ≈ 3.00, hence δ = 3.00λ . (c) Because the path difference is an integer multiple of the wavelength, the intensity at point P is a maximum. 14.3 Intensity Distribution Consider the double-slit experiment shown in Figure 14.3.1. Figure 14.3.1 Double-slit interference

The total instantaneous electric field E at the point P on the screen is equal to the vector sum of the two sources:E=E+E.The magnitude of the Poynting vector flux S is proportional to the square of the total field. S∝E2=(E,+E2)2=E+E+2E,·E2 (14.2.10) Taking the time-average of S,the intensity of the light at P is I=(S)∝(E〉+(E)+2(E·E,〉 (14.2.11) The term 2EE2)represents the correlation between the two light waves.For incoherent light sources,since there is no definite phase relation between E and E2,the cross term vanishes,and the intensity due to the incoherent source is simply the sum of the two individual intensities, Line=+12. (14.2.12) For coherent sources,the term 2EE)is non-zero.In fact,for constructive interference,E=E,,and the resulting intensity is 1=411, (14.2.13) which is four times greater than the intensity due to a single source.When destructive interference takes place,E=-E2,andEE,and the total intensity becomes I=1-211+1=0, (14.2.14) as expected. Suppose that the waves emerged from the slits are coherent sinusoidal plane waves.Let the electric field components of the wave from slits 1 and 2 at P be given by E=E sin(ot), (14.2.15) and E2=E。sin(ot+φ), (14.2.16) respectively,where the waves from both slits are assumed to have the same amplitude Eo. For simplicity,we have chosen the point P to be the origin,so that the kx dependence in the wave function is eliminated.Because the wave from slit 2 has traveled an extra 14-9
14-9 The total instantaneous electric field E at the point P on the screen is equal to the vector sum of the two sources: E = E1 + E2 . The magnitude of the Poynting vector flux S is proportional to the square of the total field, 2 2 2 2 1 2 1 2 1 2 S ∝ E = (E + E ) = E + E + 2E ⋅E . (14.2.10) Taking the time-average of S , the intensity I of the light at P is 2 2 1 2 1 2 I = S ∝ E + E + 2 E ⋅E . (14.2.11) The term 1 2 2 E ⋅E represents the correlation between the two light waves. For incoherent light sources, since there is no definite phase relation between E1 and E2 , the cross term vanishes, and the intensity due to the incoherent source is simply the sum of the two individual intensities, inc 1 2 I = I + I . (14.2.12) For coherent sources, the term 1 2 2 E ⋅E is non-zero. In fact, for constructive interference, E1 = E2 , and the resulting intensity is 1 I = 4I , (14.2.13) which is four times greater than the intensity due to a single source. When destructive interference takes place, E1 = −E2 , and 1 2 1 E ⋅E ∝ −I , and the total intensity becomes 1 1 1 I = I − 2I + I = 0 , (14.2.14) as expected. Suppose that the waves emerged from the slits are coherent sinusoidal plane waves. Let the electric field components of the wave from slits 1 and 2 at P be given by E1 = E0 sin(ωt) , (14.2.15) and 2 0 E = E sin(ωt +φ) , (14.2.16) respectively, where the waves from both slits are assumed to have the same amplitude E0 . For simplicity, we have chosen the point P to be the origin, so that the kx dependence in the wave function is eliminated. Because the wave from slit 2 has traveled an extra

distance 8 to P,E2 has an extra phase constant o relative to E,which traveled from slit 1. For constructive interference,a path difference of 8=A would correspond to a phase shift of o=2.This implies that the ratio of path difference to wavelength is equal to the ratio of phase shift to2π, 60 (14.2.17) 12π Therefore the phase shift is 0= 61 dsine. (14.2.18) Assuming that both fields point in the same direction,the total electric field may be obtained by using the superposition principle discussed in Section 13.5, E=E+E2=E[sin(@t)+sin(@t+)=2E cos(/2)sin(t+/2)(14.2.19) where we have used the trigonometric identity sina+sinB=2sin m (14.2.20) The intensity I is proportional to the time-average of the square of the total electric field, I(E2)=4E2cos(/2)(sin(@t+/2)=2Ecos(/2). (14.2.21) Therefore the intensity is 1=1cos2(0/2), (14.2.22) where /o is the maximum intensity on the screen.Substitute Eq.(14.2.18)into Eq. (14.2.22)yielding I=Icos(πdsin6/) (14.2.23) The plot of the ratio I/I as a function of dsine/A is shown in Figure 14.3.2. 14-10
14-10 distance δ to P , E2 has an extra phase constant φ relative to E1 , which traveled from slit 1. For constructive interference, a path difference of δ = λ would correspond to a phase shift of φ = 2π . This implies that the ratio of path difference to wavelength is equal to the ratio of phase shift to 2π , 2 δ φ λ π = . (14.2.17) Therefore the phase shift is 2 2 d sin π π φ δ θ λ λ = = . (14.2.18) Assuming that both fields point in the same direction, the total electric field may be obtained by using the superposition principle discussed in Section 13.5, E = E1 + E2 = E0 ⎡sin(ωt) + sin(ωt + φ) ⎣ ⎤ ⎦ = 2E0 cos(φ / 2)sin(ωt + φ / 2) (14.2.19) where we have used the trigonometric identity sinα + sinβ = 2sin α + β 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ cos α − β 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ . (14.2.20) The intensity I is proportional to the time-average of the square of the total electric field, I ∝ E2 = 4E0 2 cos2 (φ / 2) sin2 (ωt + φ / 2) = 2E0 2 cos2 (φ / 2). (14.2.21) Therefore the intensity is I = I0 cos2 (φ / 2) , (14.2.22) where 0 I is the maximum intensity on the screen. Substitute Eq. (14.2.18) into Eq. (14.2.22) yielding I = I0 cos2 (πd sinθ / λ) . (14.2.23) The plot of the ratio I / I0 as a function of d sinθ / λ is shown in Figure 14.3.2