
6.641,Electromagnetic Fields,Forces,and Motion Prof.Markus Zahn Lecture 8:Magnetization I.Magnetic Dipoles 木L=m。wR12=-2mm e v=wRi中 R 21= ew 2n Figure 5-16 The orbiting electron has its magnetic moment m in the direction opposite to its angular momentum L because the current is opposite to the electron's velocity. Courtesy of Krieger Publishing.Used with permission. m =/ds Figure 5-14 A magnetic dipole consists of a small circulating current loop.The magnetic moment is in the direction normal to the loop by the right-hand rule. Courtesy of Krieger Publishing.Used with permission. 6.641,Electromagnetic Fields,Forces,and Motion Lecture 8 Prof.Markus Zahn Page 1 of 13
6.641, Electromagnetic Fields, Forces, and Motion Lecture 8 Prof. Markus Zahn Page 1 of 13 6.641, Electromagnetic Fields, Forces, and Motion Prof. Markus Zahn Lecture 8: Magnetization I. Magnetic Dipoles Courtesy of Krieger Publishing. Used with permission. Courtesy of Krieger Publishing. Used with permission

Diamagnetism e 1=2 eo 2元 ,me1R2i.=22R2i=e9Ri /0 Angular Momentum [=mRi,x=mR(R)x=mR, (Fxp) 、 2mem e linear momentum L is quantized in units of h=6.62x10-34 joule-sec 2π (Planck's constant) e且- m=2m eh eh≈9.3x10-24amp-m2 2π(2)m。4πme Bohr magneton ms (smallest unit of magnetic moment) Imagine all Bohr magnetons in sphere of radius R aligned.Net magnetic moment is m=me 台aRp Ao Avogadro's number 6.023 x 1026 molecules per kilogram-mole M Total mass molecular weight of sphere For iron:p =7.86 x 103 kg/m3,Mo=56 Figure 9.0.1 (a)Current i in loop of -R radius R gives dipole moment m.(b) 2R Spherical material of radius R has dipole moment approximated as the sum of atomic (a) (b) dipole moments Courtesy of Hermann A.Haus and James R.Melcher.Used with permission. 6.641,Electromagnetic Fields,Forces,and Motion Lecture 8 Prof.Markus Zahn Page 2 of 13
6.641, Electromagnetic Fields, Forces, and Motion Lecture 8 Prof. Markus Zahn Page 2 of 13 Diamagnetism Angular Momentum ( ) _ __ _ 2 r rz L=mRi v=m R R i i =m R i ee e φ ⎛ ⎞ × ω× ω ⎜ ⎟ ⎝ ⎠ (r p× ) = m 2me e − linear momentum L is quantized in units of h 34 , h = 6.62 x10 joule sec 2 − − π (Planck’s constant) Bohr magneton mB (smallest unit of magnetic moment) Imagine all Bohr magnetons in sphere of radius R aligned. Net magnetic moment is 3 0 B 0 4 A mm R 3 M ⎛ ⎞ = πρ ⎜ ⎟ ⎝ ⎠ Total mass molecular weight of sphere For iron: ρ =7.86 x 103 kg/m3 , M0=56 Courtesy of Hermann A. Haus and James R. Melcher. Used with permission. Avogadro’s number = 6.023 x 1026 molecules per kilogram−mole ω − ω − π π π π ω _ 2 z e e e I= = , m= I R i = 2 2 2 π − ω _ 2 _ 2 z z e R Ri= i 2 ( ) − ≈ − 24 9.3 x10 amp π π 2 e ee e L e h eh m= = = m 2m 2 2 m 4 m

For a current loop m=izR2=m专R2p先 ,Ao→i=m3 }7.8610 6.023×1026 ForR=10cm→i=9.3×102 56 1.05 x 105 Amperes Thus,an ordinary piece of iron can have the same magnetic moment as a current loop of radius 10 cm of 105 Amperes current. B.Magnetic Dipole Field H=Hom 2cos0ir+sin0io 4πr30 (multiply top bottom by Ho) Electric Dipole Field E= 2cos0 ir+sin0 io 4πc.r3 Analogy p→μom P=Np=M=Nm,N =of magnetic dipoles/volume 1 Polarization Magnetization II.Maxwell's Equations with Magnetization EQS MOS (e目)=pu-V.p 7.(可=-7(闪 Po=-V.P(Polarization or paired Pm=-V.(Ho M)(magnetic charge charge density) density) n[旧-E门=-n[F-p]+如 n[,-f】=-n[你-)】 6.641,Electromagnetic Fields,Forces,and Motion Lecture 8 Prof.Markus Zahn Page 3 of 13
6.641, Electromagnetic Fields, Forces, and Motion Lecture 8 Prof. Markus Zahn Page 3 of 13 For a current loop 2 3 0 0 B B 0 0 4 4 A A m=i R =m R i=m R 3 M 3M π πρ ⇒ ρ For R = 10 cm ( ) ⎛ ⎞ ( × ) ⇒× × ⎜ ⎟ ⎝ ⎠ 26 -24 3 4 6.023 10 i = 9.3 10 .1 7.86 10 3 56 = 1.05 x 105 Amperes Thus, an ordinary piece of iron can have the same magnetic moment as a current loop of radius 10 cm of 105 Amperes current. B. Magnetic Dipole Field _ _ 0 r 3 0 m H = 2 cos i sin i 4 r θ µ ⎡ ⎤ θ+ θ ⎢ ⎥ π µ ⎣ ⎦ (multiply top & bottom by µ0 ) Electric Dipole Field θ ⎡ ⎤ θ+ θ ⎢ ⎥ π ε ⎣ ⎦ _ _ r 3 0 p E = 2 cos i sin i 4 r Analogy p m → µ0 P = Np M = Nm ⇒ , N = # of magnetic dipoles / volume Polarization Magnetization II. Maxwell’s Equations with Magnetization EQS ∇ ρ− i i ( ) ε0 u E= P ∇ ρ −∇ i p = P (Polarization or paired charge density) ( ) ⎡ ⎤ ⎡ ⎤ − − −+ ⎢ ⎥ ⎣ ⎦ ⎢ ⎥ ⎣ ⎦ i i ε α b a b n E E =n P P 0 s σ u MQS ∇ − i i (µ0 0 H= M ) ∇ µ( ) ρ −∇ µ m = i( 0 M) (magnetic charge density) ( ) ( ) α b a b n H H =n M M 0 0 ⎡ ⎤⎡ ⎤ − −µ − ⎢ ⎥⎢ ⎥ ⎣ ⎦⎣ ⎦ i i µ

0p=-n[p-p] cm=-n你-] VxH-j xE-品h何+网 MOS Equations B=(H+M)Magnetic flux density B has units of Teslas(1 Tesla =10,000 Gauss) 7.B=0 n[6-B]=0 VxE-_0B Γat vxH=j (total fiux) III.Magnetic Field Intensity along Axis of a Uniformly Magnetized Cylinder d/2 H: d/2 R Figure 9.3.1 (a)Cylinder of circular cross-section uniformly magnetized in the direction of its axis.(b)Axial distribution of scalar magnetic potential and(c)axial magnetic field intensity.For these distributions,the cylinder length is assumed to be equal to its diameter. 6.641,Electromagnetic Fields,Forces,and Motion Lecture 8 Prof.Markus Zahn Page 4 of 13
6.641, Electromagnetic Fields, Forces, and Motion Lecture 8 Prof. Markus Zahn Page 4 of 13 ( ) a b sm 0 =n M M ⎡ ⎤ σ −µ − ⎢ ⎥ ⎣ ⎦ i ∇ ×H=J ( ) ∂ ∇× − µ + ∂ E= H M 0 t MQS Equations B= H M µ + 0 ( ) Magnetic flux density B has units of Teslas (1 Tesla = 10,000 Gauss) ∇ = iB 0 a a n B B =0 ⎡ ⎤ − ⎢ ⎥ ⎣ ⎦ i B E = t ∂ ∇× − ∂ ∇ × H=J III. Magnetic Field Intensity along Axis of a Uniformly Magnetized Cylinder ⎡ ⎤ σ− − ⎢ ⎥ ⎣ ⎦ i a b sp =n P P λ λ ∫ i S d v = , = B da dt (total flux)

om=-n网-)→m亿=2)=,Mg om(2=-5)=-oM。 7xH=j=0→H=-VΨ 7(可=-2平=pm=-7.( - 驰了a-2rs的2ro 4πoF-r 二+ 4元4oF-r oM。2πr'dr e o-egp -登- Ψ(z) Mo/2{R+d-[R2+d2]2} -d/2 d/2 6.641,Electromagnetic Fields,Forces,and Motion Lecture 8 Prof.Markus Zahn Page 5 of 13
6.641, Electromagnetic Fields, Forces, and Motion Lecture 8 Prof. Markus Zahn Page 5 of 13 ⎧ ⎫ ⎡ ⎤⎡ ⎤ ⎪ ⎪ ⎛⎞ ⎛⎞ ⎨ ⎬ ⎢ ⎥⎢ ⎥ + − −− − + + ++ ⎜⎟ ⎜⎟ ⎪ ⎪ ⎝⎠ ⎝⎠ ⎣ ⎦⎣ ⎦ ⎩ ⎭ 1 1 2 2 2 2 M0 2 2 dd dd = Rz z Rz z 2 22 22 σ − µ − ⇒σ µ i ( ) ( ) a b sm 0 sm 0 0 = n M M z= = M d 2 ( ) σ − − sm 0 0 z= = M d 2 µ ∇ ⇒ xH= J=0 H= −∇ Ψ ∇ µ −µ ∇ Ψ ρ −∇ µ ( ) i( ) 2 00 m 0 H= = = M ( ) −ρ ρ ( ) ∇ Ψ ⇒Ψ µ πµ − ∫ 2 m m 0 V' 0 r ' dV ' = r = 4 r r' ( ) σ π σ −π ( ) ( ) Ψ + πµ − πµ − ∫ ∫ R R sm sm r'=0 0 0 r'=0 z = 2 r ' dr ' z = 2 r ' dr ' d d 2 2 z = 4 r r' 4 r r' µ π µ π − ⎡⎤ ⎡ ⎛ ⎞ ⎛ ⎞ πµ + − ⎢⎥ ⎢ πµ + + ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ⎣⎦ ⎣ ∫ ∫ R R 0 o 0 o 1 1 2 2 2 2 r'=0 r'=0 2 2 0 0 M 2 r ' dr ' M 2 r ' dr ' = d d 4 r' z 4 r' z 2 2 ⎤ ⎥ ⎥⎦ ( ) ( ) ⎡ + + ⎤ ⎣ ⎦ ⎡ ⎤ + + ⎣ ⎦ ∫ 1 2 2 2 1 2 2 2 r ' dr ' = r' z a r' z a ( ) = = ⎧ ⎫ ⎪ ⎪ ⎡ ⎤⎡ ⎤ ⎛ ⎞ ⎛ ⎞ Ψ −− ⎨ ⎬ ⎢ ⎥⎢ ⎥ + + ⎜ ⎟ ⎜ ⎟ ⎪ ⎪ ⎢ ⎥⎢ ⎥ ⎝ ⎠ ⎝ ⎠ ⎣ ⎦⎣ ⎦ ⎩ ⎭ R R 1 1 2 2 2 2 0 2 2 r' 0 r' 0 M d d z = r' + z r' z 2 2 2
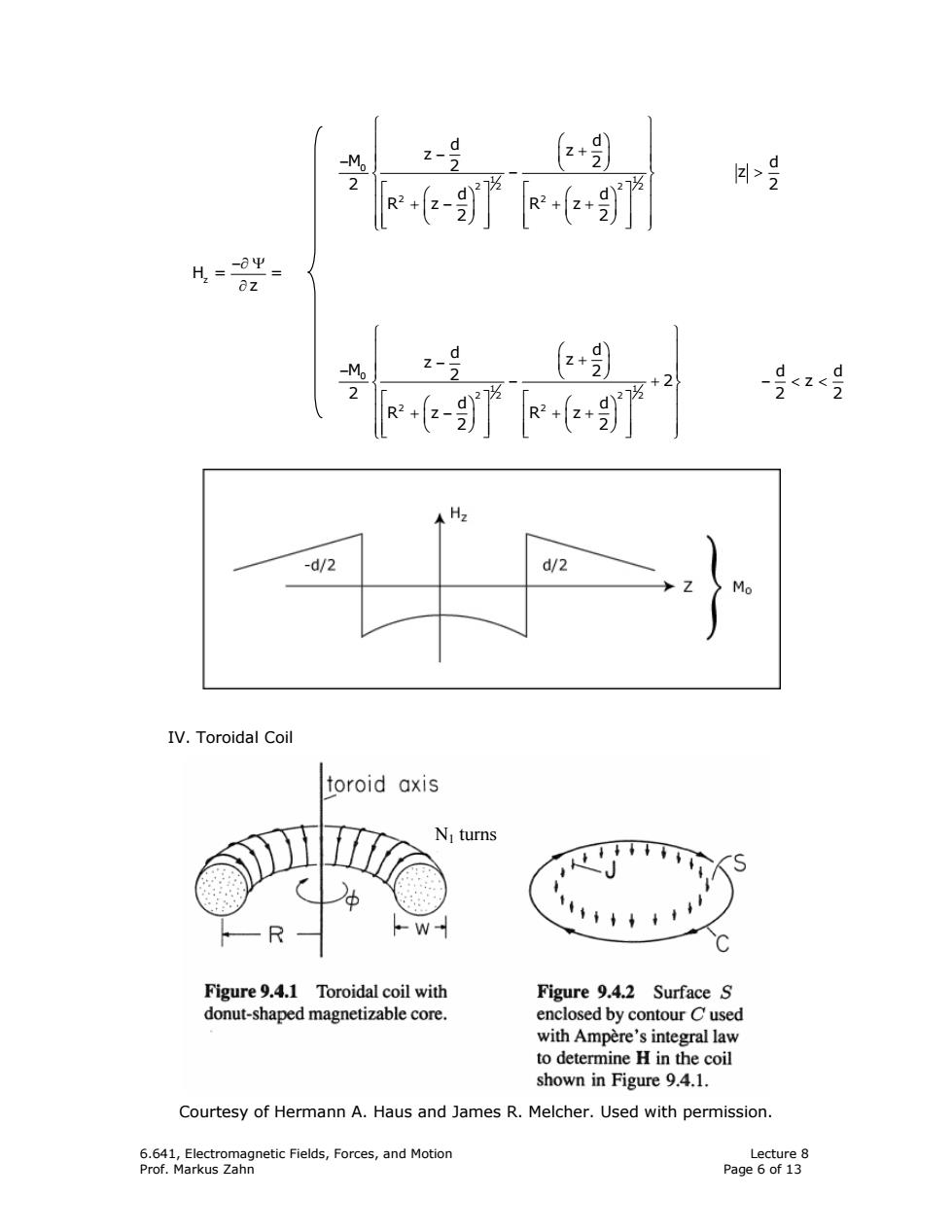
G9 - A>9 H=-0Ψ= 0z -盯 -<2 -d/2 d/2 IV.Toroidal Coil toroid axis N:turns Figure 9.4.1 Toroidal coil with Figure 9.4.2 Surface S donut-shaped magnetizable core. enclosed by contour C used with Ampere's integral law to determine H in the coil shown in Figure 9.4.1. Courtesy of Hermann A.Haus and James R.Melcher.Used with permission. 6.641,Electromagnetic Fields,Forces,and Motion Lecture 8 Prof.Markus Zahn Page 6 of 13
6.641, Electromagnetic Fields, Forces, and Motion Lecture 8 Prof. Markus Zahn Page 6 of 13 ⎧ ⎫ ⎪ ⎪ ⎛ ⎞ − + ⎜ ⎟ − ⎝ ⎠ ⎨ ⎬ − > ⎪ ⎪ ⎡ ⎤⎡ ⎤ ⎛⎞ ⎛⎞ ⎢ ⎥⎢ ⎥ +− ++ ⎜⎟ ⎜⎟ ⎝⎠ ⎝⎠ ⎩ ⎭ ⎣ ⎦⎣ ⎦ 0 1 1 2 2 2 2 2 2 d d z z M 2 2 d z 2 2 d d Rz Rz 2 2 ⎧ ⎫ ⎪ ⎪ ⎛ ⎞ − + ⎜ ⎟ − ⎝ ⎠ ⎨ ⎬ − + − << ⎪ ⎪ ⎡ ⎤⎡ ⎤ ⎛⎞ ⎛⎞ ⎢ ⎥⎢ ⎥ +− ++ ⎜⎟ ⎜⎟ ⎝⎠ ⎝⎠ ⎩ ⎭ ⎣ ⎦⎣ ⎦ 0 1 1 2 2 2 2 2 2 d d z z M 2 2 d d 2 z 2 22 d d Rz Rz 2 2 IV. Toroidal Coil Courtesy of Hermann A. Haus and James R. Melcher. Used with permission. −∂ Ψ ∂ H= = z z N1 turns

H.di=H,2xr=NiH=2r2R NiNi D*B元w2 4 入=N2D=N2B元w 4 N2 N 0000000 R1 R Figure 9.4.3 Demonstration in which the B-H curve is traced out in the sinusoidal steady state. Courtesy of Hermann A.Haus and James R.Melcher.Used with permission. V=1R1=R H,2πR N (V=Horizontal voltage to oscilloscope) -盘=,R+义=V+R,C0 dt rR》。=0R,C张a=RG (V=Vertical voltage to oscilloscope) s TW2 4-N2B 1元w2 V.=R2Cz4-N,B 6.641,Electromagnetic Fields,Forces,and Motion Lecture 8 Prof.Markus Zahn Page 7 of 13
6.641, Electromagnetic Fields, Forces, and Motion Lecture 8 Prof. Markus Zahn Page 7 of 13 φ φ π⇒ ≈ π π ∫ i v 1 1 1 C Ni Ni H dl = H 2 r = N i H = 2r 2R Courtesy of Hermann A. Haus and James R. Melcher. Used with permission. ( ) φ π H 11 1 H 1 H2 R V = i R = R V =Horizontal voltage to oscilloscope N 2 v 2 2 2v v2 2 d dV v = =i R V =V R C dt dt λ + + If ( ) 2 v 2 2 2 2 2 2 v v 2 1 d dV R R C = R C V V =Vertical voltage to oscilloscope C dt dt λ >> ⇒ ≈ ⇒ λ ω π Φ ≈ 2 w B 4 π λ Φ 2 2 2 w =N =N B 4 π 2 2 w = N 4 B π v 2 1 w V = N B RC 4 2 2 2 Vv V2 VH N1 R1 R2 i1 i2 N2 C2 - - + + + -

Figure 9.4.4 Typical magnetization curve without hysteresis.For typical 103H ferromagnetic solids,the saturation flux density is in the range of 1-2 Tesla.For ferromagnetic domains suspended in a liquid,it is .02-.04 Tesla. Courtesy of Hermann A.Haus and James R.Melcher.Used with permission. tB (c) Figure 9.4.6 Magnetization characteristic (d) for material showing hysteresis with typical b values of Br and He given in Table 9.4.2. (d) The curve is obtained after many cycles of sinusoidal excitation in apparatus such as that of Figure 9.4.3.The trajectory is traced out in response to a sinusoidal current,as shown by the inset. Courtesy of Hermann A.Haus and James R.Melcher.Used with permission. Figure 9.4.5 Polycrystalline ferromagnetic material viewed at the domain level.In applied the absence of an applied magnetic field, the domain moments tend to cancel.(This eld presumes that the material has not been left in a magnetized state by a previously applied field.)As a field is applied,the domain walls shift,giving rise to a net magnetization.In ideal materials,saturation results as all of the domains combine into one.In materials used for bulk fabrication of transformers,imperfections prevent the realization of this state. Courtesy of Hermann A.Haus and James R.Melcher.Used with permission. 6.641,Electromagnetic Fields,Forces,and Motion Lecture 8 Prof.Markus Zahn Page 8 of 13
6.641, Electromagnetic Fields, Forces, and Motion Lecture 8 Prof. Markus Zahn Page 8 of 13 Courtesy of Hermann A. Haus and James R. Melcher. Used with permission. Courtesy of Hermann A. Haus and James R. Melcher. Used with permission. Courtesy of Hermann A. Haus and James R. Melcher. Used with permission

V.Magnetic Circuits Contour of integration of Ampere's law D Ho N turns H=5 Flux leaving Closed surface S has zero net flux through it Flux entering S L Current i passes perpendicularly through contour Ntimes Faraday's law evaluated for dashed contour following N turn coil in the direction of the current Figure 6-8 The magnetic field is zero within an infinitely permeable magnetic core and is constant in the air gap if we neglect fringing.The flux through the air gap is constant at every cross section of the magnetic circuit and links the N turn coil N times. In iron core: H=0 limB=ui三 1山0 B finite ∮H.di=Hs=Ni→H=NI Φ=oHDd=to Dd N ∮B.da=0 天=Nw=bgD0N1L=子=gD心 s 6.641,Electromagnetic Fields,Forces,and Motion Lecture 8 Prof.Markus Zahn Page 9 of 13
6.641, Electromagnetic Fields, Forces, and Motion Lecture 8 Prof. Markus Zahn Page 9 of 13 V. Magnetic Circuits In iron core: H=0 lim B = H µ→∞ µ ⇒ B finite v∫ i ⇒ Ni H dl = Hs = Ni H = s µ Φ µ 0 0 Dd N = H Dd = s i S B da = 0 ∫ i v µ µ λ λΦ ⇒ 0 0 Dd 2 2 Dd =N = N i L= = N s i s

VI.Reluctance R=Ni=s (length) Dd (permeability)(cross-sectionalarea) [Reluctance,analogous to resistance] 中 N turns H41 1= 41a1D =M Contour for ←52→2■ 2 Series evaluating Ampere's law H2d2D 交=NM=中绿1+见2】 Depth D a 中=雪网+92) 2=2D N turns 乎=Ni 41a1D Paths for evaluation of Ampere's circuital Parallel Depth D law which give us that Hy=H2 Ni/s (b) Figure 6-11 Magnetic circuits are most easily analyzed from a circuit approach where (a)reluctances in series add and()permeances in parallel add. A.Reluctances In Series 41aD' R2=5 42a2D Ni Φ=双+风 ∮H.d=Hs,+H252=Ni 6.641,Electromagnetic Fields,Forces,and Motion Lecture 8 Prof.Markus Zahn Page 10 of 13
6.641, Electromagnetic Fields, Forces, and Motion Lecture 8 Prof. Markus Zahn Page 10 of 13 VI. Reluctance [Reluctance, analogous to resistance] R ( ) Φ µ ( ) ( ) − 0 Ni s length == = Dd permeability cross sec tional area A. Reluctances In Series R1 µ 1 1 1 s = , a D R2 µ 2 2 2 s = a D Φ + 1 2 Ni = R R + ∫ i v 11 22 C H dl = H s H s = Ni Series Parallel