
6.641,Electromagnetic Fields,Forces,and Motion Prof.Markus Zahn Lecture 13:Magnetoquasistatic Forces I.MQS Energy Method of Forces V= dx dt (b) (a)Magnetoquasistatic system having one electrical terminal pair and one mechanical degree of freedom.(b)Schematic representation of MQS subsystem with coupling to external mechanical system represented by a mechanical terminal pair. A.Circuit Approach v-0-品(0-L(e+9 dt p=i=L()+包 dt -L6{ =2(r小r9 =2ge i-0+5w=(0P,专=图 dt d =L=5-围 、d 6.641,Electromagnetic Fields,Forces,and Motion Lecture 13 Prof.Markus Zahn Page 1 of 14
6.641, Electromagnetic Fields, Forces, and Motion Lecture 13 Prof. Markus Zahn Page 1 of 14 6.641, Electromagnetic Fields, Forces, and Motion Prof. Markus Zahn Lecture 13: Magnetoquasistatic Forces I. MQS Energy Method of Forces A. Circuit Approach () () λ (ξ) ⎡ ⎤ ξ ξ+ ⎣ ⎦ d d di dL v= = L i =L i dt dt dt dt ( ) (ξ) ξ + 2 di dL p = vi = L i i dt dt ( ) ( ) 2 2 d 1 dL =L i i dt 2 dt ⎛ ⎞ ξ ξ + ⎜ ⎟ ⎝ ⎠ ( ) ( ) 2 2 d1 1 dL = Li i dt 2 2 dt ⎡ ⎤ ξ ξ + ⎢ ⎥ ⎣ ⎦ ( ) ( ) 2 2 d1 1 d dL = Li i dt 2 2 d dt ⎡ ⎤ ξ ξ ξ + ⎢ ⎥ ⎣ ⎦ ξ ( ) ( ) m 2 2 m dW d1 1 dL vi= f W = L i , f = i dt dt 2 2 d ξ ξ ξ ξ +⇒ ξ ξ ( ) ( ) ξ ξ λ ξ⇒ ξ 2 1 dL =L i f = i 2 d

河想 =-品{Xl B.Energy Method vi.idds aWm i=o a形 01 λ=constant =constant 本d战=0 →5 f=0 w.ds ∫id -cons tant 1=L 入 w府=z λ2 5-w/ ah=constant -(e 6.641,Electromagnetic Fields,Forces,and Motion Lecture 13 Prof.Markus Zahn Page 2 of 14
6.641, Electromagnetic Fields, Forces, and Motion Lecture 13 Prof. Markus Zahn Page 2 of 14 ( ) ( ) 2 2 1 dL = 2 d L λ ξ ξ ξ ( ) = 1 d 2 1 2 d L ⎡ ⎤ − λ ⎢ ⎥ ξ ξ ⎣ ⎦ B. Energy Method ξ ξ λ ξ + ⇒ λ− ξ m m d d dW vi = i = f dW = id f d dt dt dt m m =constant W W , i= f = = constant ξ ξ ∂ ∂ − ∂λ ∂ξ λ 0 ξ λ= ξ= − ξ+ λ m ∫ ∫ 0 cons tan t W = f d id ( ) i = L λ ξ ( ) ( ) ξ = λ λ λ ξ ξ ∫ 2 m cons tan t W= d= L 2L ( ) m 2 cons tan t W 1 d f= = 1 2 d L ξ λ = −∂ ⎛ ⎞ − λ ⎜ ⎟ ∂ξ ξ ξ ⎝ ⎠

1 dL() d II.Force on a Wire over a Perfectly Conducting Plane Depth D 00 Figure 11.7.3 Cross-section of perfectly conducting current-carrying wire over a perfectly conducting ground plane. Courtesy of Hermann A.Haus and James R.Melcher.Used with permission. [See Haus Melcher p.343, take 12 of Eq.(12)which is the inductance between 2 cylinders] A.Energy Method 专r但0 1 de 4πR )-1 f。 Figure 11.7.4 The force tending to levitate the wire of Figure 11.7.3 as a 2 3 function of the distance to the ground plane ξ/R- normalized to the radius R of wire. Courtesy of Hermann A.Haus and James R.Melcher.Used with permission. 6.641,Electromagnetic Fields,Forces,and Motion Lecture 13 Prof.Markus Zahn Page 3 of 14
6.641, Electromagnetic Fields, Forces, and Motion Lecture 13 Prof. Markus Zahn Page 3 of 14 ( ) ( ) 2 2 1 1 dL = 2 d L ⎛ ⎞ ξ −λ−⎜ ⎟ ξ ξ ⎝ ⎠ ( ) 2 1 dL i 2 d ξ = ξ II. Force on a Wire over a Perfectly Conducting Plane Courtesy of Hermann A. Haus and James R. Melcher. Used with permission. ( ) 2 0D L = ln 1 2 RR ⎡ ⎤ µ ξ ξ ⎛ ⎞ ξ +− ⎢ ⎥ ⎜ ⎟ π ⎝ ⎠ ⎣ ⎦ A. Energy Method ( ) ( ) 2 2 0 2 1 1 dL i D f= i = 2 d 4R 1 R ξ ξ µ ξ π ξ − [See Haus & Melcher p. 343, take ½ of Eq. (12) which is the inductance between 2 cylinders] Courtesy of Hermann A. Haus and James R. Melcher. Used with permission. Depth D

B.Method of Images Approach with Lorentz Force Depth D Image current i R ● 个 o 7777777777777777777777777777 777777777777777∞ 2-R2 x image current-i f iD oi) =2D-2D 2π(2a) 4πa 4π√g2-R2 C.Demonstration:Steady State Magnetic Leviation Figure 11.7.5 When the pancake coil is driven by an ac current,it floats above the aluminum plate.In this experiment,the coil consists of 250 turns of No.10 aluminum wire with an outer radius of 16 cm and an inner one of 2.5 cm.The aluminum sheet has a thickness of 1.3 cm.With a 60 Hz current i of about 20 amp rms.the height above the plate is 2 cm. Courtesy of Hermann A.Haus and James R.Melcher.Used with permission. 6.641,Electromagnetic Fields,Forces,and Motion Lecture 13 Prof.Markus Zahn Page 4 of 14
6.641, Electromagnetic Fields, Forces, and Motion Lecture 13 Prof. Markus Zahn Page 4 of 14 B. Method of Images Approach with Lorentz Force ( ) 2 2 00 0 2 2 i iD iD f = iD = = 2 2a 4 a 4 R ξ ⎛ ⎞ µµ µ ⎜ ⎟ ⎝ ⎠ π π πξ− C. Demonstration: Steady State Magnetic Leviation Courtesy of Hermann A. Haus and James R. Melcher. Used with permission
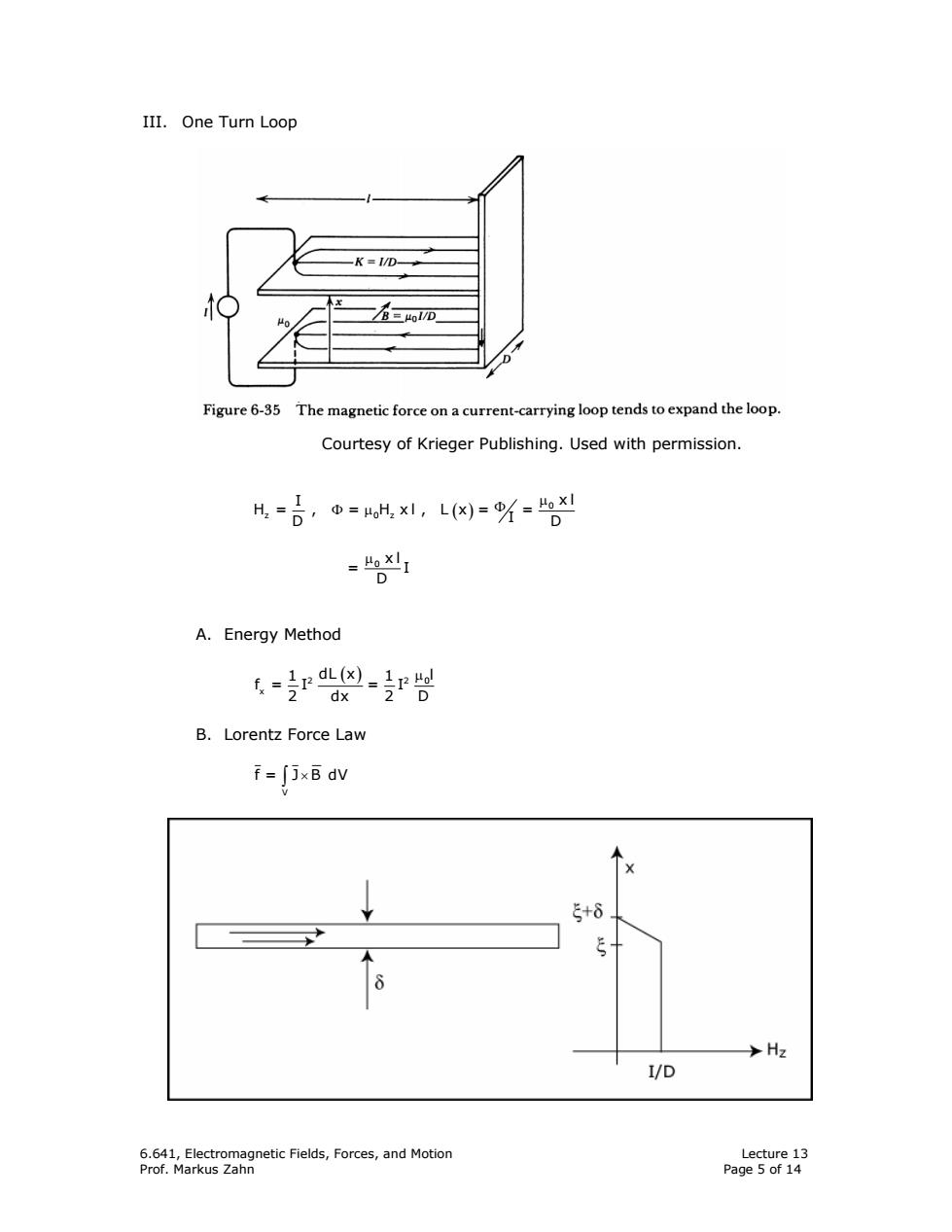
III.One Turn Loop K=I/D- B=LoI/D. Figure 6-35 The magnetic force on a current-carrying loop tends to expand the loop. Courtesy of Krieger Publishing.Used with permission. H=6,=Hx1,L)=%= D HoxlI D A.Energy Method 专rA-r时 dx 2 D B.Lorentz Force Law f=∫JxB dV 5+8 →H2 I/D 6.641,Electromagnetic Fields,Forces,and Motion Lecture 13 Prof.Markus Zahn Page 5 of 14
6.641, Electromagnetic Fields, Forces, and Motion Lecture 13 Prof. Markus Zahn Page 5 of 14 III. One Turn Loop Courtesy of Krieger Publishing. Used with permission. ( ) µ Φ µ Φ 0 z 0z I x l H = , = H xl , L x = = D D I µ0 x l = I D A. Energy Method ( ) 2 2 0 x 1 1 dL x l f= I = I 2 dx 2 D µ B. Lorentz Force Law V f = J B dV × ∫

Model srace currenKs volume current of small thickness I Jy=D8 xH=j→股=-小,=→片=5x-(传+训 I f.H dx dy dz -器}k-e+ax ÷号-6时+ ++号+的 12 comes from integrating uniform volume current over small thickness 8 General formula:f=[KxBav ds 0 For our case:B= B2+B业= 2 2 6.641,Electromagnetic Fields,Forces,and Motion Lecture 13 Prof.Markus Zahn Page 6 of 14
6.641, Electromagnetic Fields, Forces, and Motion Lecture 13 Prof. Markus Zahn Page 6 of 14 Model surface current y I K = D as volume current of small thickness δ y I J = Dδ ( ) ( ) z y z H I I H=J = J = H = x xD D ∂ ∇× ⇒ − − ⇒ − − ξ + δ ∂ δδ 0 I I = D D −µ δ ( ) ( ) + x= x lD ξ δ ξ ⎛ ⎞ ⎜ ⎟ − ξ+δ ⎝ ⎠ δ ∫ dx ( ) 2 2 0 2 x I l x = x D 2 ξ+δ =ξ −µ ⎡ ⎤ ⎢ ⎥ − ξ+δ δ ⎣ ⎦ ( ) ()() 2 2 2 2 0 2 I l = D 2 2 −µ ⎡ ⎤ ξ+δ ξ ⎢ ⎥ − − ξ+δ +ξ ξ+δ δ ⎣ ⎦ ( ) 2 2 2 0 2 I l 1 = D 2 2 −µ ⎡ ⎤ ξ ⎢ ⎥ − ξ + δ + + ξδ δ ⎣ ⎦ 2 0 2 2 I l 1 = D 2 −µ ⎡ ⎤ − δ ⎢ ⎥ δ ⎣ ⎦ 2 0 S 1 1 I l = f = K B dS 2D 2 µ +⇒ × ∫ ½ comes from integrating uniform volume current over small thickness δ General formula: av S f = K B dS × ∫ 0 For our case: metal air av air B B 1 B= =B 2 2 + µ x y0z ∫ V f = J H dx dy dz
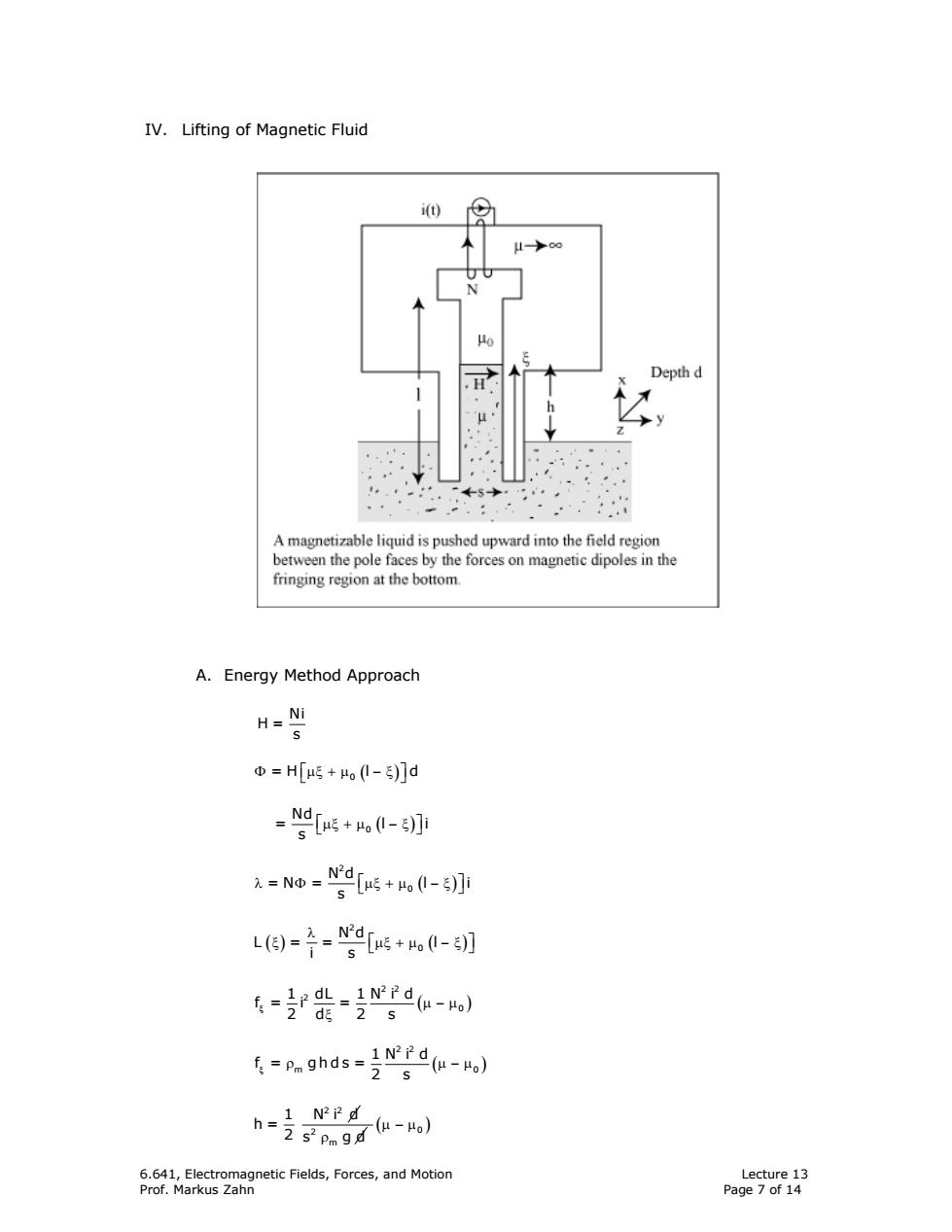
IV.Lifting of Magnetic Fluid i(t) →∞ o Depth d A magnetizable liquid is pushed upward into the field region between the pole faces by the forces on magnetic dipoles in the fringing region at the bottom. A.Energy Method Approach H=Ni Φ=H[μg+μo0-)]d =9[贱+,0-5明 =No=g2[g+0- L同=子=9[5+0- 专=吃登-9e-w) .gndd(w) -i时 6.641,Electromagnetic Fields,Forces,and Motion Lecture 13 Prof.Markus Zahn Page 7 of 14
6.641, Electromagnetic Fields, Forces, and Motion Lecture 13 Prof. Markus Zahn Page 7 of 14 IV. Lifting of Magnetic Fluid A. Energy Method Approach Φ µξ + µ − ξ =H l d ⎡ ⎤ 0 ( ) ⎣ ⎦ ⎡ ⎤ µξ + µ − ξ ( ) ⎣ ⎦ 0 Nd = li s λ Φ µξ + µ − ξ ⎡ ⎤ ( ) ⎣ ⎦ 2 0 N d =N = l i s ( ) ( ) λ ξ µ⎡ ⎤ ξ + µ − ξ ⎣ ⎦ 2 0 N d L == l i s ξ ( ) µ − µ ξ 2 2 2 0 1 dL 1 N i d f= i = 2d 2 s ξ ρ ( ) µ−µ 2 2 m 0 1N i d f = ghds = 2 s 2 2 1 Ni d h = 2 ρ 2 s gd m ( ) µ−µ0 Ni H = s

B.Magnetization force Fx Ho (M.V)Hx =0 z 7×H=j=0→=a ay Ox B=明=h佰+网==(片-1 E=[能-農+货,袋 =供-[2w+ f=[F dx dy dz -但2212+)axyz X=-y=0Z=0 s,儿 2 =-)dN吧 2。 -u-)a 6.641,Electromagnetic Fields,Forces,and Motion Lecture 13 Prof.Markus Zahn Page 8 of 14
6.641, Electromagnetic Fields, Forces, and Motion Lecture 13 Prof. Markus Zahn Page 8 of 14 B. Magnetization force F= M H X0 x µ ∇ ( ) i xxx 0x y z HHH =M M M xyz ⎡ ⎤ ∂∂∂ µ ++ ⎢ ⎥ ⎣ ⎦ ∂∂∂ = 0 z ∂ ∂ ∂ ∂ ∇× ⇒ ∂ ∂ Hx Hy H= J=0 = y x x y X 0x y H H F= M M x x ⎡ ⎤ ∂ ∂ µ + ⎢ ⎥ ∂ ∂ ⎣ ⎦ ( ) ⎛ ⎞ µ µ µ +⇒ − ⎜ ⎟ ⎝ ⎠ µ 0 0 B= H= H M M= 1 H x y x0 x y 0 0 H H F= 1H 1H x x ⎡ ⎤ ⎛⎞ ⎛⎞ µ µ ∂ ∂ µ − +− ⎢ ⎥ ⎜⎟ ⎜⎟ µ ∂µ ∂ ⎣ ⎦ ⎝⎠ ⎝⎠ ( ) 2 2 0 xy 0 1 = 1 HH x 2 ⎛ ⎞ µ ∂ ⎡ ⎤ µ− + ⎜ ⎟ ⎢ ⎥ ⎝ ⎠ µ ∂ ⎣ ⎦ x x f = F dx dy dz ∫ ( ) ( ) h sd 0 2 2 x y x y 0z 0 = H H dx dy dz 2 x =−∞ = = µ−µ ∂ + ∂ ∫ ∫∫ ( ) ( ) =−∞ µ−µ + h 0 2 2 x y x = ds H H 2 (µ−µ0 ) = ds 2 2 2 2 N i s ( ) µ−µ 2 2 0 1 Ni = d 2 s
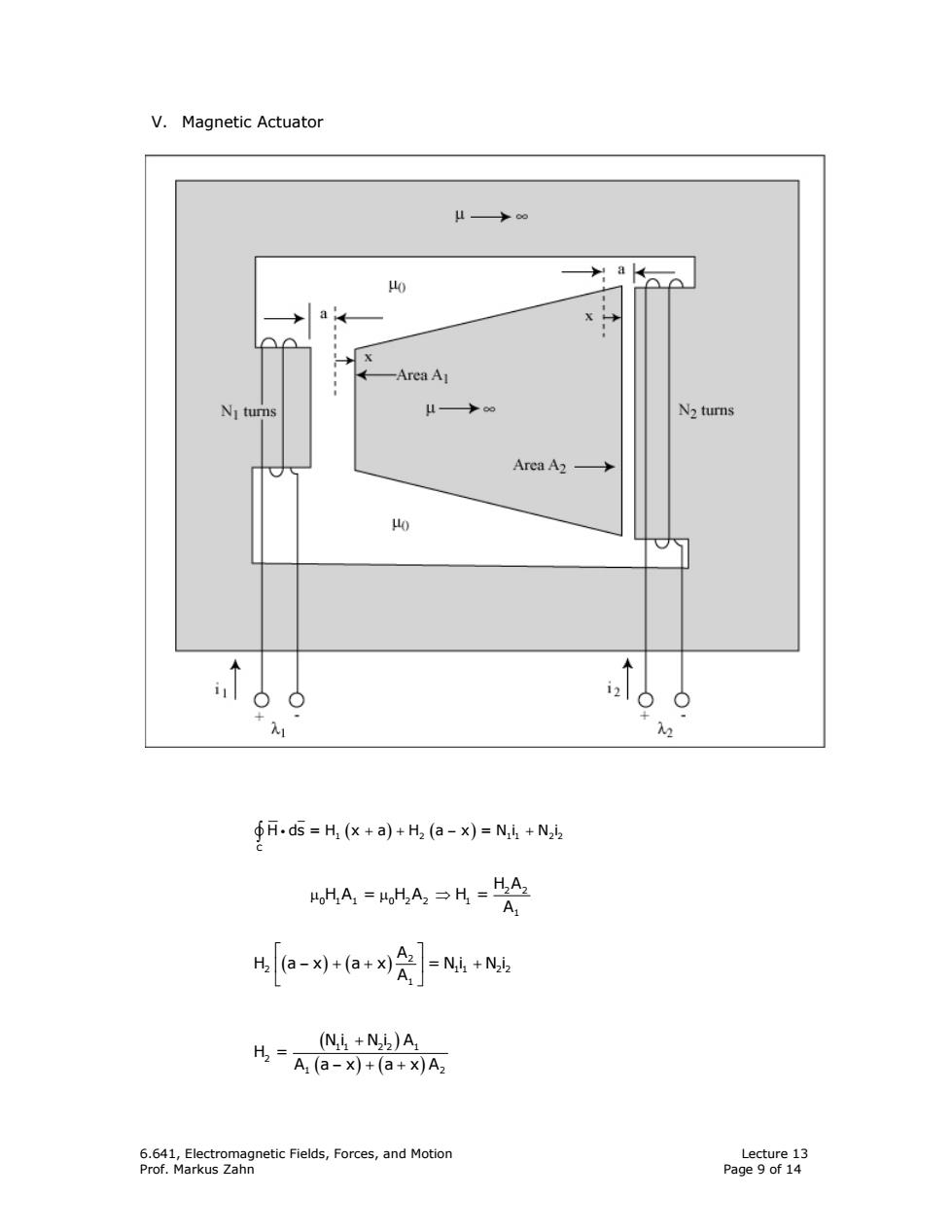
V.Magnetic Actuator μ→∞ a长 0 ←-Area A N]turns μ→∞ N2 turns Area A2→ 40 M .d5=H仪+a+片(a-x)=N4+Nh A=A=H=冷 h[a-刘+(a+2] =N,i +N2iz (Ni +Ni2)A H=A(a-x为)+a+x)A: 6.641,Electromagnetic Fields,Forces,and Motion Lecture 13 Prof.Markus Zahn Page 9 of 14
6.641, Electromagnetic Fields, Forces, and Motion Lecture 13 Prof. Markus Zahn Page 9 of 14 V. Magnetic Actuator 1 2 11 22 ( ) ( ) C H ds = H x a H a x = N i N i ++ − + ∫ i v 2 2 011 02 2 1 1 H A HA = HA H = A µ µ⇒ ( )( ) 2 2 11 22 1 A H a x a x =Ni Ni A ⎡ ⎤ ⎢ ⎥ −++ + ⎣ ⎦ ( ) ( )( ) 11 22 1 2 1 2 Ni Ni A H = A a x a xA + −++
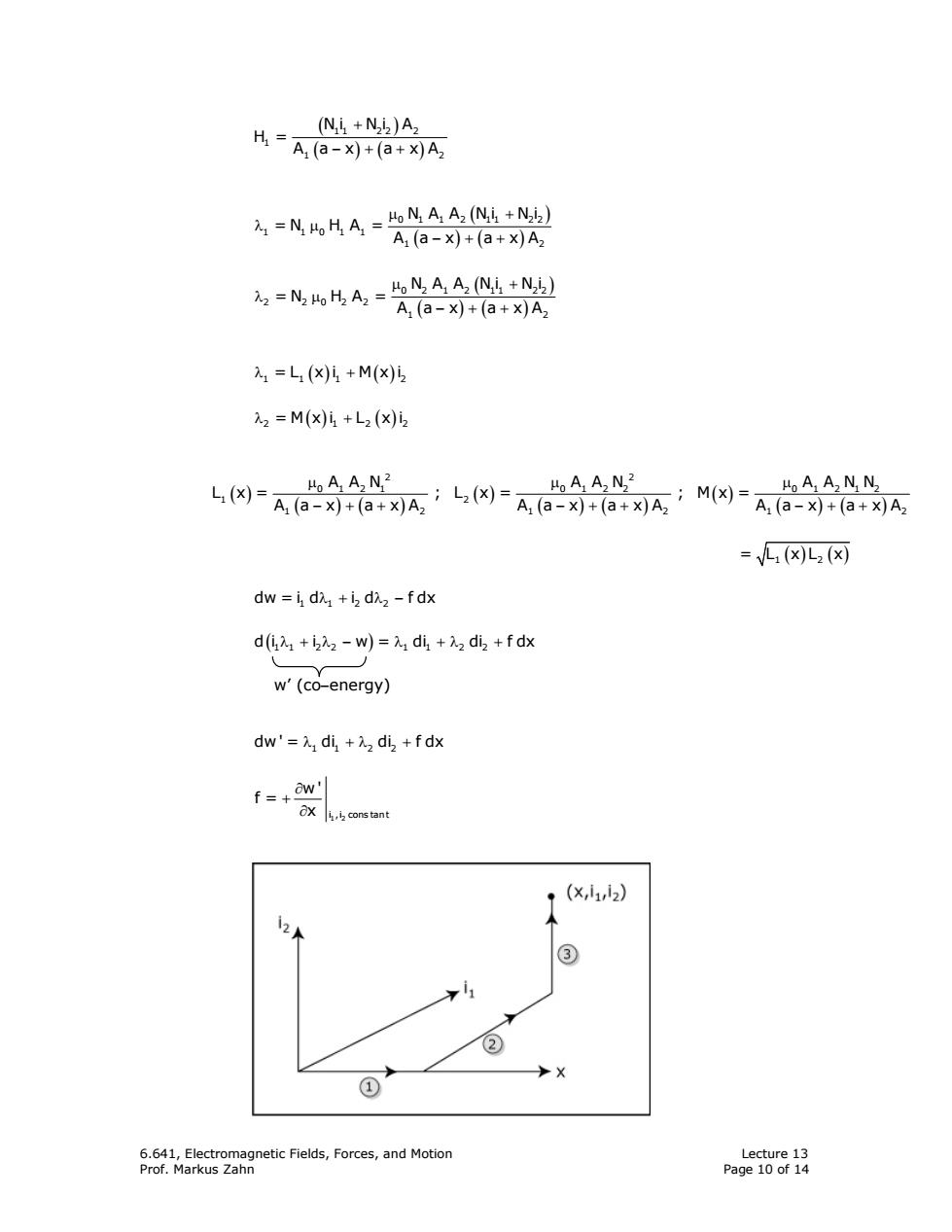
(Ni+N22)A2 H-A(a-x)+(a+为A =N,HA=。NAA+N) A(a-x)+(a+)A2 女=A=会奇哈 入1=L(X)5+M(X)52 2=M(x)1+L2(x)12 b肉=A阳岭8:与肉=AB产8:M网A。合8不 “AA2N22 =1(x)L2(x dw=i da+i dx2-fdx d(i+iz-w)=di +72 diz +f dx w'(co-energy) dw'=λ1di+2di2+fdx f=+0w' ox i,iconstant (x,,2) ③ ③ ① 6.641,Electromagnetic Fields,Forces,and Motion Lecture 13 Prof.Markus Zahn Page 10 of 14
6.641, Electromagnetic Fields, Forces, and Motion Lecture 13 Prof. Markus Zahn Page 10 of 14 ( ) ( )( ) 11 22 2 1 1 2 Ni Ni A H = A a x a xA + −++ ( ) ( )( ) 0 1 1 2 11 22 1 101 1 1 2 N A A Ni Ni =N H A = A a x a xA µ + λ µ −++ ( ) ( )( ) 0 2 1 2 11 22 2 202 2 1 2 N A A Ni Ni =N H A = A a x a xA µ + λ µ −++ () () λ + 111 2 =L x i M x i () () λ + 2 12 2 =M x i L x i ( ) ( )( ) ( ) ( )( ) ( ) ( )( ) 2 2 0 1 21 0 1 22 0 1 212 1 2 1 2 1 21 2 A A N A A N A A NN L x= ; L x= ; Mx= A a x a xA A a x a xA A a x a xA µ µµ −++ −++ −++ = L xL x 1 2 () () dw = i d i d f dx 112 2 λ+ λ− ( ) λ + λ − λ +λ + d i i w = di di f dx 11 22 1 1 2 2 w’ (co−energy) dw' = di di f dx 11 22 λ +λ + 1 2 i ,i cons tan t w' f = x ∂ + ∂