《电磁学》课程教学资源（教材讲义）交流电 Chapter 12 Alternating-Current Circuits

Chapter 12 Alternating-Current Circuits 12.1 AC Sources.… 12-2 12.2 Simple AC circuits............. 12-3 12.2.1 Purely Resistive load.... 12-3 12.2.2 Purely Inductive Load. 12-5 12.2.3 Purely Capacitive Load. 12-7 12.3 The RLC Series Circuit....... 12-9 12.3.1 Impedance...... 12-12 12.3.2 Resonance..... 12-13 12.4 Power in an AC circuit.. 12-14 12.4.1 Width of the Peak 12-16 12.5 Transformer............ 12-17 12.6 Parallel RLC Circuit... 12-19 12.7 Summary......... 12-22 12.8 Problem-Solving Tips 12-24 12.9 Solved Problems.......... 12-26 12.9.1 RLC Series Circuit 12-26 12.9.2 RLC Series Circuit 12-27 12.9.3 Resonance........... 12-28 12.9.4 RL High-Pass Filter 12-29 12.9.5 RLC Circuit............... 12-30 12.9.6 RL Filter....... 12-33 12.10 Conceptual Questions 12-35 12.11 Additional Problems...... 12-36 12.11.1 Reactance of a Capacitor and an Inductor 12-36 12.11.2 Driven RLC Circuit Near Resonance..... 12-36 12.11.3 RC Circuit.… 12-37 12.11.4 Black Box............... 12-37 12.11.5 Parallel RL Circuit........ 。 12-38 12.11.6 LC Circuit........... 12-39 12.11.7 Parallel RC Circuit. 12-39 12.11.8 Power Dissipation...... 12-40 l2.11.9 FM Antenna… 12-40 12.11.10 Driven RLC Circuit. 12-41 12-1

Chapter 12 Alternating-Current Circuits 12.1 AC Sources....................................................................................................... 12-2 12.2 Simple AC circuits............................................................................................ 12-3 12.2.1 Purely Resistive load.................................................................................. 12-3 12.2.2 Purely Inductive Load................................................................................ 12-5 12.2.3 Purely Capacitive Load.............................................................................. 12-7 12.3 The RLC Series Circuit..................................................................................... 12-9 12.3.1 Impedance................................................................................................ 12-12 12.3.2 Resonance ................................................................................................ 12-13 12.4 Power in an AC circuit.................................................................................... 12-14 12.4.1 Width of the Peak..................................................................................... 12-16 12.5 Transformer .................................................................................................... 12-17 12.6 Parallel RLC Circuit........................................................................................ 12-19 12.7 Summary......................................................................................................... 12-22 12.8 Problem-Solving Tips..................................................................................... 12-24 12.9 Solved Problems............................................................................................. 12-26 12.9.1 RLC Series Circuit ................................................................................... 12-26 12.9.2 RLC Series Circuit ................................................................................... 12-27 12.9.3 Resonance ................................................................................................ 12-28 12.9.4 RL High-Pass Filter.................................................................................. 12-29 12.9.5 RLC Circuit.............................................................................................. 12-30 12.9.6 RL Filter................................................................................................... 12-33 12.10 Conceptual Questions................................................................................... 12-35 12.11 Additional Problems..................................................................................... 12-36 12.11.1 Reactance of a Capacitor and an Inductor ............................................. 12-36 12.11.2 Driven RLC Circuit Near Resonance..................................................... 12-36 12.11.3 RC Circuit .............................................................................................. 12-37 12.11.4 Black Box............................................................................................... 12-37 12.11.5 Parallel RL Circuit.................................................................................. 12-38 12.11.6 LC Circuit............................................................................................... 12-39 12.11.7 Parallel RC Circuit ................................................................................. 12-39 12.11.8 Power Dissipation .................................................................................. 12-40 12.11.9 FM Antenna ........................................................................................... 12-40 12.11.10 Driven RLC Circuit.............................................................................. 12-41 12-1

Alternating-Current Circuits 12.1 AC Sources In Chapter 10 we learned that changing magnetic flux can induce an emf according to Faraday's law of induction.In particular,if a coil rotates in the presence of a magnetic field,the induced emf varies sinusoidally with time and leads to an alternating current (AC),and provides a source of AC power.The symbol for an AC voltage source is An example of an AC source is V(t)=Vo sinot (12.1.1) where the maximum valueVo is called the amplitude.The voltage varies between Vo and since a sine function varies between +1 and-1.A graph of voltage as a function of time is shown in Figure 12.1.1. (t) Vo Figure 12.1.1 Sinusoidal voltage source The sine function is periodic in time.This means that the value of the voltage at time t will be exactly the same at a later time t'=t+T where T is the period.The frequency, f,defined as f=1/T,has the unit of inverse seconds(s),or hertz(Hz).The angular frequency is defined to be @=2zf. When a voltage source is connected to an RLC circuit,energy is provided to compensate the energy dissipation in the resistor,and the oscillation will no longer damp out.The oscillations of charge,current and potential difference are called driven or forced oscillations. After an initial "transient time,"an AC current will flow in the circuit as a response to the driving voltage source.The current,written as 12-2

Alternating-Current Circuits 12.1 AC Sources In Chapter 10 we learned that changing magnetic flux can induce an emf according to Faraday’s law of induction. In particular, if a coil rotates in the presence of a magnetic field, the induced emf varies sinusoidally with time and leads to an alternating current (AC), and provides a source of AC power. The symbol for an AC voltage source is An example of an AC source is 0 V t( ) =V sinωt (12.1.1) where the maximum valueV is called the amplitude. The voltage varies between and since a sine function varies between +1 and −1. A graph of voltage as a function of time is shown in Figure 12.1.1. 0 V0 −V0 Figure 12.1.1 Sinusoidal voltage source The sine function is periodic in time. This means that the value of the voltage at time t will be exactly the same at a later time t t ′ = +T where T is the period. The frequency, f , defined as f = 1/T , has the unit of inverse seconds (s−1 ), or hertz (Hz). The angular frequency is defined to be ω = 2π f . When a voltage source is connected to an RLC circuit, energy is provided to compensate the energy dissipation in the resistor, and the oscillation will no longer damp out. The oscillations of charge, current and potential difference are called driven or forced oscillations. After an initial “transient time,” an AC current will flow in the circuit as a response to the driving voltage source. The current, written as 12-2

I(t)=lo sin(ot-φ) (12.1.2) will oscillate with the same frequency as the voltage source,with an amplitude lo and phase o that depends on the driving frequency. 12.2 Simple AC circuits Before examining the driven RLC circuit,let's first consider the simple cases where only one circuit element (a resistor,an inductor or a capacitor)is connected to a sinusoidal voltage source. 12.2.1 Purely Resistive load Consider a purely resistive circuit with a resistor connected to an AC generator,as shown in Figure 12.2.1.(As we shall see,a purely resistive circuit corresponds to infinite capacitance C=co and zero inductance L=0.) R VR(O) (t)='osinωt Figure 12.2.1 A purely resistive circuit Applying Kirchhoffs loop rule yields V(t)-V(t)=V(t)-I()R=0 (12.2.1) where Ve(t)=I(t)R is the instantaneous voltage drop across the resistor.The instantaneous current in the resistor is given by (V(Vaosin ot sin ot R (12.2.2) R where VRo =Vo,and Igo=VRo/R is the maximum current.Comparing Eq.(12.2.2)with Eq.(12.1.2),we find=0,which means that I(t)and V(t)are in phase with each other,meaning that they reach their maximum or minimum values at the same time.The time dependence of the current and the voltage across the resistor is depicted in Figure 12.2.2(a). 12-3

0 I t( ) = I sin(ωt −φ) (12.1.2) will oscillate with the same frequency as the voltage source, with an amplitude 0 I and phase φ that depends on the driving frequency. 12.2 Simple AC circuits Before examining the driven RLC circuit, let’s first consider the simple cases where only one circuit element (a resistor, an inductor or a capacitor) is connected to a sinusoidal voltage source. 12.2.1 Purely Resistive load Consider a purely resistive circuit with a resistor connected to an AC generator, as shown in Figure 12.2.1. (As we shall see, a purely resistive circuit corresponds to infinite capacitance C = ∞ and zero inductance L = 0 .) Figure 12.2.1 A purely resistive circuit Applying Kirchhoff’s loop rule yields ( ) ( ) ( ) ( ) 0 V t VR R − t = − V t I t R = (12.2.1) where is the instantaneous voltage drop across the resistor. The instantaneous current in the resistor is given by ( ) ( ) V t R R = I t R 0 0 ( ) sin ( ) sin R R R V t V t R I t R R I t ω = = = ω (12.2.2) where , and VR0 =V0 R0 R0 I =V R is the maximum current. Comparing Eq. (12.2.2) with Eq. (12.1.2), we findφ = 0 , which means that ( ) RI t and are in phase with each other, meaning that they reach their maximum or minimum values at the same time. The time dependence of the current and the voltage across the resistor is depicted in Figure 12.2.2(a). ( ) VR t 12-3

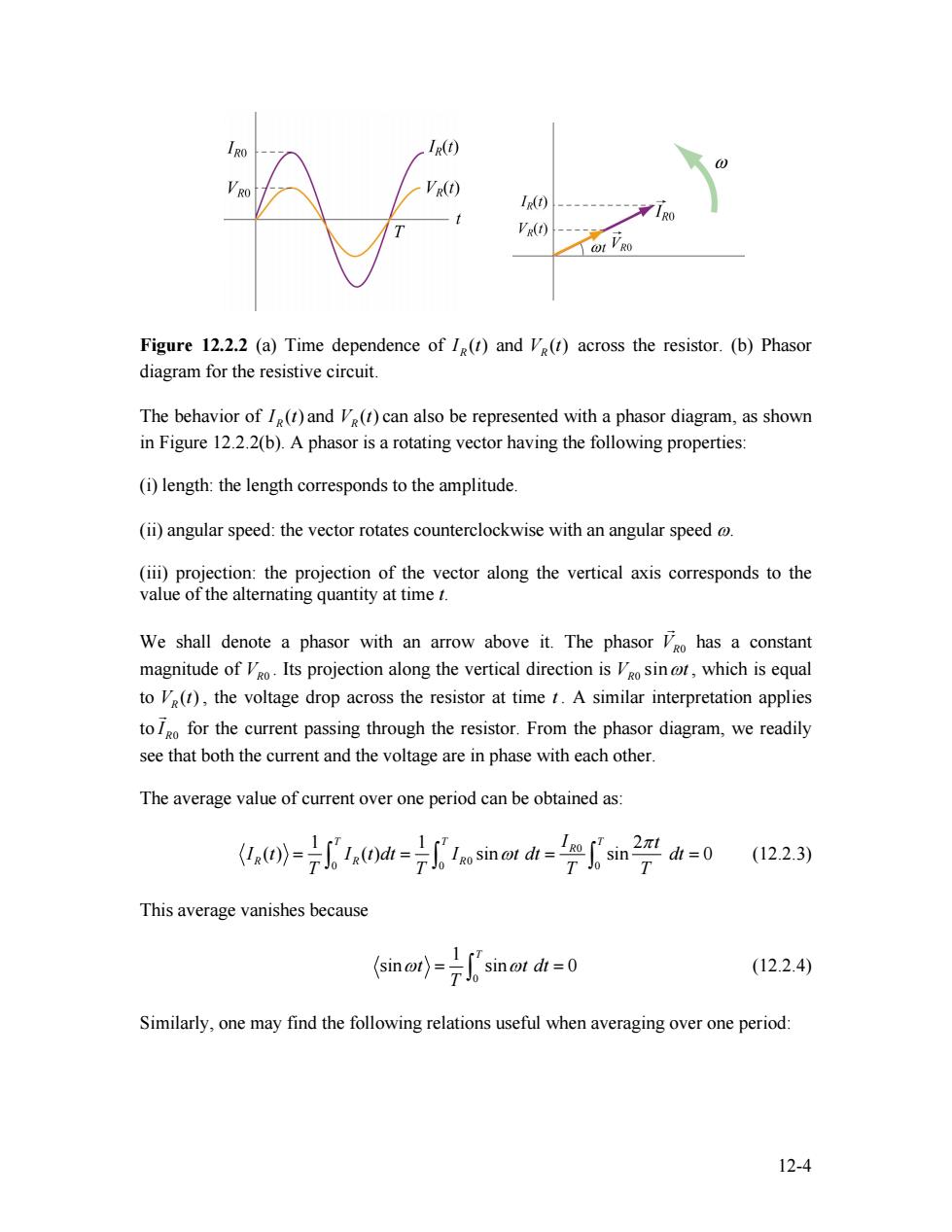
RO IR(t) V RO VR(t) I(t) ----10 VR(A) Figure 12.2.2 (a)Time dependence of I(t)and Ve(t)across the resistor.(b)Phasor diagram for the resistive circuit. The behavior of I(t)and V(t)can also be represented with a phasor diagram,as shown in Figure 12.2.2(b).A phasor is a rotating vector having the following properties: (i)length:the length corresponds to the amplitude. (ii)angular speed:the vector rotates counterclockwise with an angular speed @ (iii)projection:the projection of the vector along the vertical axis corresponds to the value of the alternating quantity at time t. We shall denote a phasor with an arrow above it.The phasor Vgo has a constant magnitude ofo Its projection along the vertical direction is osin,which is equal to V(t),the voltage drop across the resistor at time t.A similar interpretation applies to for the current passing through the resistor.From the phasor diagram,we readily see that both the current and the voltage are in phase with each other. The average value of current over one period can be obtained as: (()(dsino d sin (12.2.3) This average vanishes because sin ot dt =0 (12.2.4) Similarly,one may find the following relations useful when averaging over one period: 12-4

Figure 12.2.2 (a) Time dependence of ( ) RI t and ( ) VR t across the resistor. (b) Phasor diagram for the resistive circuit. The behavior of ( ) RI t and can also be represented with a phasor diagram, as shown in Figure 12.2.2(b). A phasor is a rotating vector having the following properties: ( ) VR t (i) length: the length corresponds to the amplitude. (ii) angular speed: the vector rotates counterclockwise with an angular speed ω. (iii) projection: the projection of the vector along the vertical axis corresponds to the value of the alternating quantity at time t. We shall denote a phasor with an arrow above it. The phasor has a constant magnitude of . Its projection along the vertical direction is VR0 G VR0 0 sin VR ωt , which is equal to , the voltage drop across the resistor at time t . A similar interpretation applies to ( ) VR t R0 I G for the current passing through the resistor. From the phasor diagram, we readily see that both the current and the voltage are in phase with each other. The average value of current over one period can be obtained as: 0 0 0 0 0 1 1 2 ( ) ( ) sin sin 0 T T T R R R R I t I t I t dt I t dt dt T T T T π = = ω = ∫ ∫ ∫ = (12.2.3) This average vanishes because 0 1 sin sin 0 T t t T ω = ω dt = ∫ (12.2.4) Similarly, one may find the following relations useful when averaging over one period: 12-4

(eosa）=cod=0 sin arcor)sin rcos (12.2.5) 如侧叫号momm(2）-月 (coi m)=oi m=os(2）=月 From the above,we see that the average of the square of the current is non-vanishing: o)=0通=%smah=sm(2）血=22 It is convenient to define the root-mean-square(rms)current as -芳 (12.2.7) In a similar manner,the rms voltage can be defined as -o-芳 (12.2.8) The rms voltage supplied to the domestic wall outlets in the United States is V'ms=120 Vat a frequencyf=60 Hz. The power dissipated in the resistor is PR(t)=Ig(t)VR(t)=IR(t)R (12.2.9) from which the average over one period is obtained as: o-2@R=5aR=R=1-g (12.2.10) R 12.2.2 Purely Inductive Load Consider now a purely inductive circuit with an inductor connected to an AC generator, as shown in Figure 12.2.3. 12-5

0 0 2 2 2 0 0 2 2 2 0 0 1 cos cos 0 1 sin cos sin cos 0 1 1 2 sin sin sin 2 1 1 2 cos cos cos 2 T T T T T T t t dt T t t t t dt T t t t dt dt T T T t t t dt dt T T T ω ω ω ω ω ω π ω ω π ω ω = = = = ⎛ ⎞ = = ⎜ ⎟ ⎝ ⎠ ⎛ ⎞ = = ⎜ ⎟ ⎝ ⎠ ∫ ∫ ∫ ∫ ∫ ∫ 1 1 = = (12.2.5) From the above, we see that the average of the square of the current is non-vanishing: 2 2 2 2 2 2 0 0 0 0 0 1 1 1 2 ( ) ( ) sin sin 2 T T T R R R R t 2 0 1 R I t I t dt I t dt I dt I T T T T π ω ⎛ ⎞ = = = ⎜ ⎟ = ⎝ ⎠ ∫ ∫ ∫ (12.2.6) It is convenient to define the root-mean-square (rms) current as 2 0 rms ( ) 2 R R I I I = t = (12.2.7) In a similar manner, the rms voltage can be defined as 2 0 rms ( ) 2 R R V V V = t = (12.2.8) The rms voltage supplied to the domestic wall outlets in the United States is at a frequency . rms V =120 V f = 60 Hz The power dissipated in the resistor is (12.2.9) 2 ( ) ( ) ( ) ( ) P t R R R R = I t V t = I t R from which the average over one period is obtained as: 2 2 2 2 rms 0 rms rms rms 1 ( ) ( ) 2 R R R V P t I t R I R I R I V R = = = = = (12.2.10) 12.2.2 Purely Inductive Load Consider now a purely inductive circuit with an inductor connected to an AC generator, as shown in Figure 12.2.3. 12-5

V(t)=Vo sin@t Figure 12.2.3 A purely inductive circuit As we shall see below,a purely inductive circuit corresponds to infinite capacitance C=oo and zero resistance R=0.Applying the modified Kirchhoff's rule for inductors, the circuit equation reads P)-y20=p0-L业=0 (12.2.11) dt which implies dlL-V④_'sinot (12.2.12) dt LL where Vo=Vo.Integrating over the above equation,we find (12.2.13) where we have used the trigonometric identity -cosot=sin @1- (12.2.14) for rewriting the last expression.Comparing Eq.(12.2.14)with Eq.(12.1.2),we see that the amplitude of the current through the inductor is L0= OL XL (12.2.15) where XL=@L (12.2.16) is called the inductive reactance.It has SI units of ohms ()just like resistance. However,unlike resistance,X,depends linearly on the angular frequency @Thus,the resistance to current flow increases with frequency.This is due to the fact that at higher 12-6

Figure 12.2.3 A purely inductive circuit As we shall see below, a purely inductive circuit corresponds to infinite capacitance and zero resistance . Applying the modified Kirchhoff’s rule for inductors, the circuit equation reads C = ∞ R = 0 ( ) ( ) ( ) 0 L L dI V t V t V t L dt − = − = (12.2.11) which implies 0 ( ) sin dIL V t VL t dt L L = = ω (12.2.12) where . Integrating over the above equation, we find VL0 =V0 0 0 0 ( ) sin cos sin 2 L L L L L V V V I t dI t dt t t L L L π ω ω ω ω ⎛ ⎞ ⎛ ⎞ ⎛ = = = − = ⎜ − ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ∫ ∫ ω ⎞ ⎟ (12.2.13) where we have used the trigonometric identity cos sin 2 t t π ω ω ⎛ − = ⎜ − ⎝ ⎠ ⎞ ⎟ (12.2.14) for rewriting the last expression. Comparing Eq. (12.2.14) with Eq. (12.1.2), we see that the amplitude of the current through the inductor is 0 0 L L L L V V I ωL X = = 0 (12.2.15) where XL =ωL (12.2.16) is called the inductive reactance. It has SI units of ohms (Ω), just like resistance. However, unlike resistance, XL depends linearly on the angular frequency ω. Thus, the resistance to current flow increases with frequency. This is due to the fact that at higher 12-6

frequencies the current changes more rapidly than it does at lower frequencies.On the other hand,the inductive reactance vanishes as approaches zero. By comparing Eq.(12.2.14)to Eq.(12.1.2),we also find the phase constant to be (12.2.17) The current and voltage plots and the corresponding phasor diagram are shown in the Figure 12.2.4 below. I() Figure 12.2.4 (a)Time dependence of I(t)and V(t)across the inductor.(b)Phasor diagram for the inductive circuit. As can be seen from the figures,the current I(t)is out of phase with V(t)by =z/2; it reaches its maximum value after V(t)does by one quarter of a cycle.Thus,we say that The current lags voltage by /2 in a purely inductive circuit 12.2.3 Purely Capacitive Load In the purely capacitive case,both resistance R and inductance L are zero.The circuit diagram is shown in Figure 12.2.5. Vc(t) V(t)=Vosin@t Figure 12.2.5 A purely capacitive circuit 12-7

frequencies the current changes more rapidly than it does at lower frequencies. On the other hand, the inductive reactance vanishes as ω approaches zero. By comparing Eq. (12.2.14) to Eq. (12.1.2), we also find the phase constant to be 2 π φ = + (12.2.17) The current and voltage plots and the corresponding phasor diagram are shown in the Figure 12.2.4 below. Figure 12.2.4 (a) Time dependence of ( ) L I t and ( ) VL t across the inductor. (b) Phasor diagram for the inductive circuit. As can be seen from the figures, the current ( ) L I t is out of phase with ( ) by VL t φ = π / 2 ; it reaches its maximum value after ( ) does by one quarter of a cycle. Thus, we say that VL t The current lags voltage by π / 2 in a purely inductive circuit 12.2.3 Purely Capacitive Load In the purely capacitive case, both resistance R and inductance L are zero. The circuit diagram is shown in Figure 12.2.5. Figure 12.2.5 A purely capacitive circuit 12-7

Again,Kirchhoff's voltage rule implies )-Ve(0=r0-0=0 (12.2.18) which yields Q(t)=CV(t)=CVc(t)=CVco sin@t (12.2.19) where Vco=.On the other hand,the current is (12.2.20) d where we have used the trigonometric identity cosot sin 0t+ (12.2.21) 2 The above equation indicates that the maximum value of the current is Ico =@CVco=- (12.2.22) Xc where 1 Xc=- (12.2.23) OC is called the capacitance reactance.It also has SI units of ohms and represents the effective resistance for a purely capacitive circuit.Note that X is inversely proportional to both C andand diverges as approaches zero. By comparing Eq.(12.2.21)to Eq.(12.1.2),the phase constant is given by (12.2.24) 2 The current and voltage plots and the corresponding phasor diagram are shown in the Figure 12.2.6 below. 12-8

Again, Kirchhoff’s voltage rule implies ( ) ( ) ( ) ( ) 0 C Q t V t V t V t C − = − = (12.2.18) which yields 0 ( ) ( ) ( ) sin Q C C t = = CV t CV t =CV ωt (12.2.19) where . On the other hand, the current is VC0 =V0 0 0 ( ) cos sin 2 C C C dQ I t CV t CV t dt π ω ω ω ω ⎛ = + = = ⎜ + ⎝ ⎠ ⎞ ⎟ (12.2.20) where we have used the trigonometric identity cos sin 2 t t π ω ω ⎛ = ⎜ + ⎝ ⎠ ⎞ ⎟ (12.2.21) The above equation indicates that the maximum value of the current is 0 0 0 C C C C V I CV X =ω = (12.2.22) where 1 XC ωC = (12.2.23) is called the capacitance reactance. It also has SI units of ohms and represents the effective resistance for a purely capacitive circuit. Note that XC is inversely proportional to both C and ω , and diverges as ω approaches zero. By comparing Eq. (12.2.21) to Eq. (12.1.2), the phase constant is given by 2 π φ = − (12.2.24) The current and voltage plots and the corresponding phasor diagram are shown in the Figure 12.2.6 below. 12-8

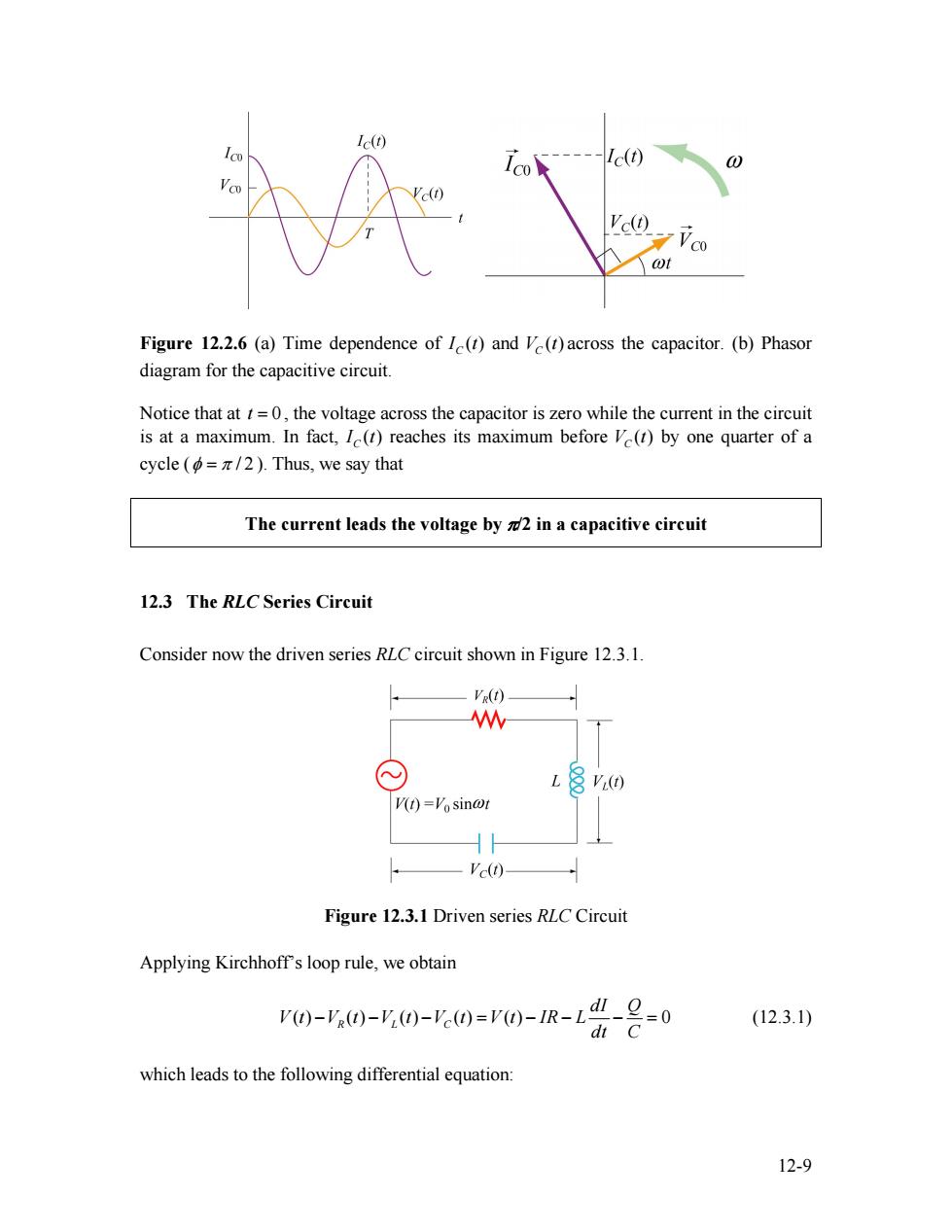
Ic(t) Ic(t) 0 Ve(t) ￥C0 wt Figure 12.2.6 (a)Time dependence of I(t)and V(t)across the capacitor.(b)Phasor diagram for the capacitive circuit. Notice that at t=0,the voltage across the capacitor is zero while the current in the circuit is at a maximum.In fact,I(t)reaches its maximum before V(t)by one quarter of a cycle (=/2).Thus,we say that The current leads the voltage by 2 in a capacitive circuit 12.3 The RLC Series Circuit Consider now the driven series RLC circuit shown in Figure 12.3.1. VR(t) W V(t)=Vosin@t Ve(t) Figure 12.3.1 Driven series RLC Circuit Applying Kirchhoffs loop rule,we obtain V)-'0)-y(0-0=r0-1R-L"-2=0 (12.3.1) dt C which leads to the following differential equation: 12-9

Figure 12.2.6 (a) Time dependence of ( ) CI t and across the capacitor. (b) Phasor diagram for the capacitive circuit. ( ) VC t Notice that at , the voltage across the capacitor is zero while the current in the circuit is at a maximum. In fact, t = 0 ( ) CI t reaches its maximum before by one quarter of a cycle ( ( ) VC t φ = π / 2 ). Thus, we say that The current leads the voltage by π/2 in a capacitive circuit 12.3 The RLC Series Circuit Consider now the driven series RLC circuit shown in Figure 12.3.1. Figure 12.3.1 Driven series RLC Circuit Applying Kirchhoff’s loop rule, we obtain ( ) ( ) ( ) ( ) ( ) 0 R L C dI Q V t V t V t V t V t IR L dt C − − − = − − − = (12.3.1) which leads to the following differential equation: 12-9

+I-Vosinot (12.3.2) d Assuming that the capacitor is initially uncharged so that I=+do/dt is proportional to the increase of charge in the capacitor,the above equation can be rewritten as do +Ra№+9=osinot C (12.3.3) d d One possible solution to Eq.(12.3.3)is Q(t)=Qcos(ot-φp) (12.3.4) where the amplitude and the phase are,respectively, '%/L Vo R-VLCy @R2+(@L-1/@C) (12.3.5) oVR2+(X-Xc)月 and tand= oi-nc (12.3.6) R @C The corresponding current is I()= d-l,sin(@t--p） (12.3.7) dt with an amplitude 10=-Qo0=- a (12.3.8) VR+(X-Xc)2 Notice that the current has the same amplitude and phase at all points in the series RLC circuit.On the other hand,the instantaneous voltage across each of the three circuit elements R,L and C has a different amplitude and phase relationship with the current,as can be seen from the phasor diagrams shown in Figure 12.3.2. 12-10

0 sin dI Q L IR V dt C + + = ωt (12.3.2) Assuming that the capacitor is initially uncharged so that I = +dQ / dt is proportional to the increase of charge in the capacitor, the above equation can be rewritten as 2 2 0 sin d Q dQ Q L R V dt dt C + + = ωt (12.3.3) One possible solution to Eq. (12.3.3) is 0 Q t( ) =Q cos(ωt −φ) (12.3.4) where the amplitude and the phase are, respectively, 0 0 0 2 2 2 2 0 2 2 / ( / ) ( 1/ ) ( 1/ ) ( ) L C V L V Q 2 R L LC R L V R X X ω ω ω ω ω ω = = + − + − = + − C (12.3.5) and 1 1 tan XL XC L R C R φ ω ω ⎛ ⎞ − = − ⎜ ⎟ = ⎝ ⎠ (12.3.6) The corresponding current is 0 ( ) sin( ) dQ I t I t dt = + = ω −φ (12.3.7) with an amplitude 0 0 0 2 ( ) L C V I Q R X X = − ω = − + − 2 (12.3.8) Notice that the current has the same amplitude and phase at all points in the series RLC circuit. On the other hand, the instantaneous voltage across each of the three circuit elements R, L and C has a different amplitude and phase relationship with the current, as can be seen from the phasor diagrams shown in Figure 12.3.2. 12-10